比赛链接
Dashboard - Codeforces Global Round 21 - Codeforces
上次状态不好,小号随便打了两题就走,前两题太水就不说了
C-Fishingprince Plays With Array(构造+贪心) 1400
题意
给你一个长度为n的数组a以及正整数m。你有两个操作
- 如果一个a_i数是m的倍数,你可以将m分成连续的\frac{a_i}{m}
- 如果有m个连续的\frac{a_i}{m},可以合成一个数a_i
问能否最后得到一个长度为k的数组b
例如:
5 2
1 2 2 4 2
4
1 4 4 2
可以将a数组的第二位和第三位的两个2合成一个4,使得a数组变成b数组。
思路
这种两个操作都是逆操作的,可以把它们都转化成最长的,也就是分解到都不能分解为止。因为如果最底层的都是一样的,那么最后合成也是可以的。例如:
n=5 m=4
a: 16,12,20,12,12
我可以转化成
4,4,4,4,3,3,3,3,5,5,5,5,3,3,3,3,3,3,3,3
但是这样太长,我们到时候保存的时候就拿pair<int,int>保存
变成{4,4},{3,4},{5,4},{3,8},第一个存值,第二个存个数。
将a,b两个数组都变成这样,然后再去比较两个是不是一样,注意:vector可以直接用==比较
代码
vector<PII> p(N),q(N);
inline PII divide(int x)
{
int res = 1;
while (x%m==0)
{
x/=m;
res *= m;
}
return {x,res};
}
inline void Case_Test()
{
cin>>n>>m;
p.clear();q.clear();
for (int i=1;i<=n;i++)
{
cin>>x;
PII res = divide(x);
if (p.size()&&p[p.size()-1].first==res.first)
p[p.size()-1].second += res.second;
else
p.push_back(res);
}
cin>>k;
for (int i=1;i<=k;i++)
{
cin>>x;
PII res = divide(x);
if (q.size()&&q[q.size()-1].first==res.first)
q[q.size()-1].second += res.second;
else
q.push_back(res);
}
if (p!=q) cout<<"No"<<endl;
else cout<<"Yes"<<endl;
}
D. Permutation Graph(ST表+分治) 1900
题意
给你一个长度为n的排列a,如果有l_i,r_i满足a[l_i],a[r_i]是区间a[l_i],a[l_i+1],...,a[r_i-1],a[r_i]中的最小值或者最大值,那么就在l_i到r_i建一条边,边权为1。问从1到n的最短距离是多少。注意,给出的数组是排列,没有相同的时候。
例如:
10
7 4 8 1 6 10 3 5 2 9
为如下图片
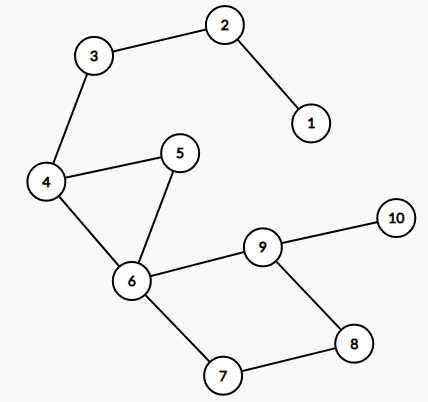
思路
我们对于上面那个样例来分析,一开始我在1...n中找到最小的最大的位置,分别是4,6,那么我不用管4和6之间了。为什么?因为哪怕中间有再多路径都不如走从4->6这一条,因为4和6已经是当前最小和最大的了。
假如有人问,能不能绕过4呢?比如从结点3到结点5——不可能,因为4是最小的。
所以这个最小和最大,完全将整个数列分割开来,只需要不断这样寻求最优解分治下去即可。
具体操作:
对于当前的dfs(int l,int r)中寻找最小值和最大值两个分界点L和R(不满足L<R则交换),然后往下继续分治找dfs(l,L),dfs(R,r),知道只有一个和两个的时候特判,一个点肯定是不足构成一个边的,如果是两个点那么就return 1。
寻找区间最小值和最大值用的是ST表,
代码
inline int MIN(int l,int r)
{
w=lg2[r-l+1];
return Min(f[l][w],f[r-(1<<w)+1][w]);
}
inline int MAX(int l,int r)
{
w=lg2[r-l+1];
return Max(g[l][w],g[r-(1<<w)+1][w]);
}
inline void init()
{
for (int i=1;i<=n;i++)
f[i][0] = g[i][0] = a[i];
for (int i=2;i<=n;i++)
lg2[i]=lg2[i>>1]+1;
for (int i=n;i>=1;i--)
for (int j=1;i+(1<<j)-1<=n;j++)
f[i][j]=Min(f[i][j-1],f[i+(1<<j-1)][j-1]),
g[i][j]=Max(g[i][j-1],g[i+(1<<j-1)][j-1]);
}
inline int dfs(int l,int r)
{
if (l==r) return 0;
if (l+1==r) return 1;
int mi = MIN(l,r), ma = MAX(l,r);
int L = pos[mi], R = pos[ma];
if (L>R) swap(L,R);
return dfs(l,L)+dfs(R,r)+1;
}
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>a[i];
pos[ a[i] ] = i;
}
init();
cout<<dfs(1,n)<<endl;
}
E. Placing Jinas(数学/组合数学) 2000
题意
有一个无限大的网络,给定一个长度为n+1的数组a[0]到a[n],保证a是非递增的,对于所有点(x,y)满足y<a[x]的点都是白色点,其他都是黑色点。
以题目中
10
12 11 8 8 6 6 6 5 3 2 1
为例。

其实就是在说第i列有a[i]个白色格子
在初始有一个小球在(0,0),你可以执行以下操作,选择一个位置在(x,y)上的小球,把它删除,并且在(x+1,y),(x,y+1)上的地方继续添加一个小球,也就是
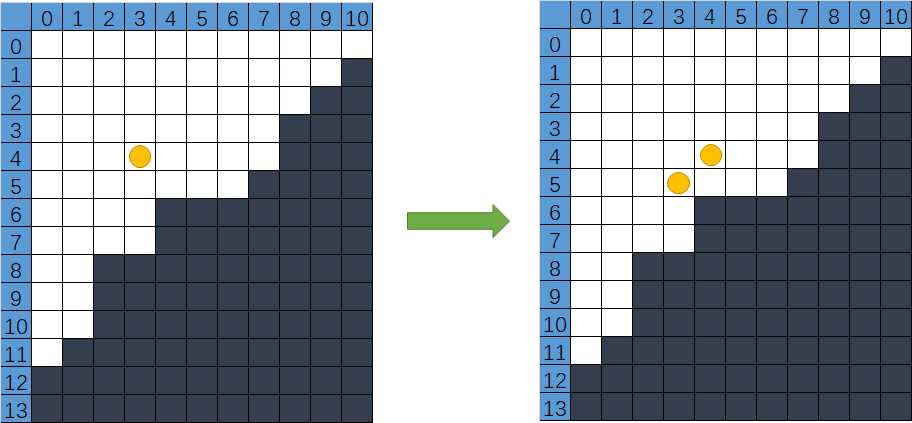
问最少多少次操作,使得白色格子上没有小球了。
思路
先分析一下,小球在(0,0)开始往外扩散的时候能得出什么样的数据?当小球在(x,y)的时候,个数与(x-1,y)与(x,y-1)有关,也就是
f[x][y] = f[x-1][y]+f[x][y-1],f[0][0]=1
也就是杨辉三角
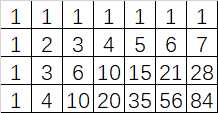
杨辉三角这个题教给我一个结论,一个矩阵和的结论:
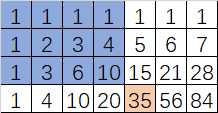
一个矩阵的和(从左上(0,0)开始到(x,y))的值为f[x][y]-1
例如上面的35-1=1+1+1+1+1+2+3+4+1+3+6+10.
所以我们能得到从(0,0)到(x,y)的矩阵和:
int cal(int x,int y)
{
x++;y++;
return (C(x+y,x)-1+mod)%mod;
}
那对于每一列我们可以优化一下,优化成一个个的矩形,如严格鸽这图:
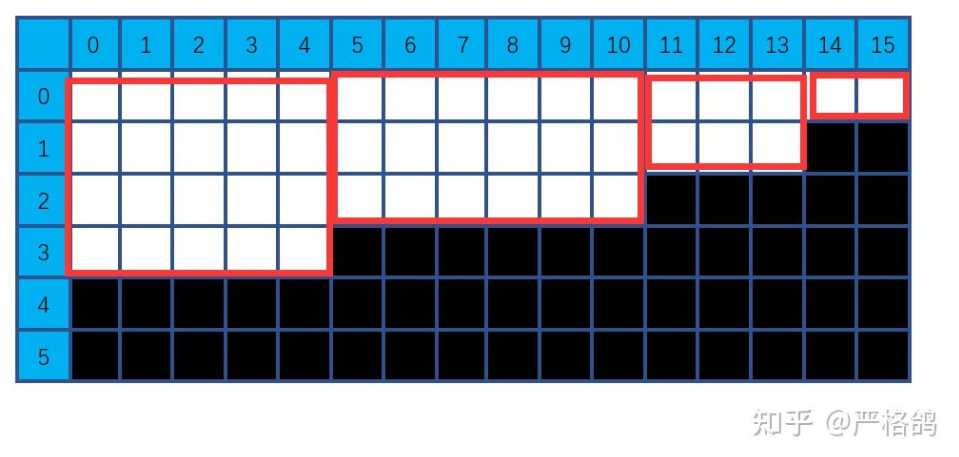
可以用map<int,vector<int>>mp处理
for (int i=0;i<=n;i++)
mp[a[i]].push_back(i);
这样对于矩形两边只需要取v.begin()和v.back()即可。
然后我们对于每个矩形求和就好。
类似于前缀和。
inline int calc(int L,int R,int k)
{
return (cal(R,k) - cal(L-1,k) + mod) % mod;
}
这里对于组合数进行预处理:
int fac[N],invfac[N],n,a[N];
inline void init()
{
fac[0] = invfac[0] = 1;
for (int i=1;i<N;i++)
fac[i] = fac[i-1]*i%mod;
invfac[N-1] = qpow(fac[N-1],mod-2,mod);
for (int i=N-2;i>=0;i--)
invfac[i] = invfac[i+1]*(i+1)%mod;
}
inline int C(int a,int b)
{
if (a<b) return 0;
return fac[a]*invfac[b]%mod*invfac[a-b]%mod;
}
代码
代码都在上面呢
主函数写一下:
map<int,vector<int>> mp;
inline void Case_Test()
{
init();
cin>>n;
for (int i=0;i<=n;i++)
cin>>a[i],a[i]--;
for (int i=0;i<=n;i++)
mp[a[i]].push_back(i);
int ans = 0;
for (auto t:mp)
{
int k = t.first, L = t.second.front(), R = t.second.back();
ans = (ans + calc(L,R,k)) % mod;
}
cout<<ans<<endl;
}
感谢
感谢严格鸽教我学代码
文章评论