最后过了一题,让排名达到了229,不错不错,一开始还以为我们都要一题寄了。
06数位DP,待补2022 杭电多校7 个人题解 更新至5题 - 严格鸽
1004.Black Magic(思维+签到)
题意:给你n个砖块,每块有左右两种颜色(黑或白),现在有一种魔法可以使得两个左右砖块进行合并变成一个砖块,当左砖块的右面和右砖块的左面都为黑的时候。
现在有四种砖块,分别是E,L,R,B分别表示(0,0),(1,0),(0,1),(1,1),1,0分别表示的是黑和白。你会得到每种个数,求对砖块进行摆放成一排,求使用魔法之后的最小个数和最大个数。
思路:
最小个数:这个时候我去找LBBBBBBR这样的,让所有的B都填入其中,这三种有两个就可以,这样子B填完了,就LR抱对即可。
最大个数:那就是LLLLLBEBEBEBBBBBRRRRRR这样的情况,L,R都往两边摆,最后没办法只能让多的B相消除,但是我也有E也可以插入其中。
代码:
别人的都很简单,我这里需要判断的有些多,其实可以合并许多的,我按照我的思路来的。
int e,l,r,b;
inline void Case_Test()
{
cin>>e>>l>>r>>b;
int t1 = e, t2 = l, t3 = r, t4 = b;
ans = e+l+r+b;
int res = b;
if ((l>0)+(r>0)+(b>0)>=2) res = b+(r>0)+(l>0);
if (res>0) ans -= res-1;
r = Max(0, r-1), l = Max(0, l-1);
if (l>0&&r>0) ans -= Min(l,r);//抱对
cout<<ans<<" ";
e = t1, l = t2, r = t3, b = t4;
ans = e+l+r+b;
ans -= Max(0, b-e-1);
cout<<ans<<endl;
}1008.Triangle Game(博弈)
题意:给你三个数a,b,c表示三角形的三边,每次可以选择一个数下降,但是要保持为非退化三角形(即有面积的三角形,不能共线,就是平时所说的三角形)。最后不能动的人输。
思路:猜nim游戏,三边不能为,所以判断(a-1)^(b-1)^(c-1)是否为0,如果是则输。
代码:
inline void Case_Test()
{
cin>>a>>b>>c;
ans = (a-1)^(b-1)^(c-1);
if (ans) cout<<"Win"<<endl;
else cout<<"Lose"<<endl;
}1003.Counting Stickmen
题意:给你一颗树,求这里面有多少个火柴人。
需要满足有一个头,两条手,一个下体(两条腿),如图:
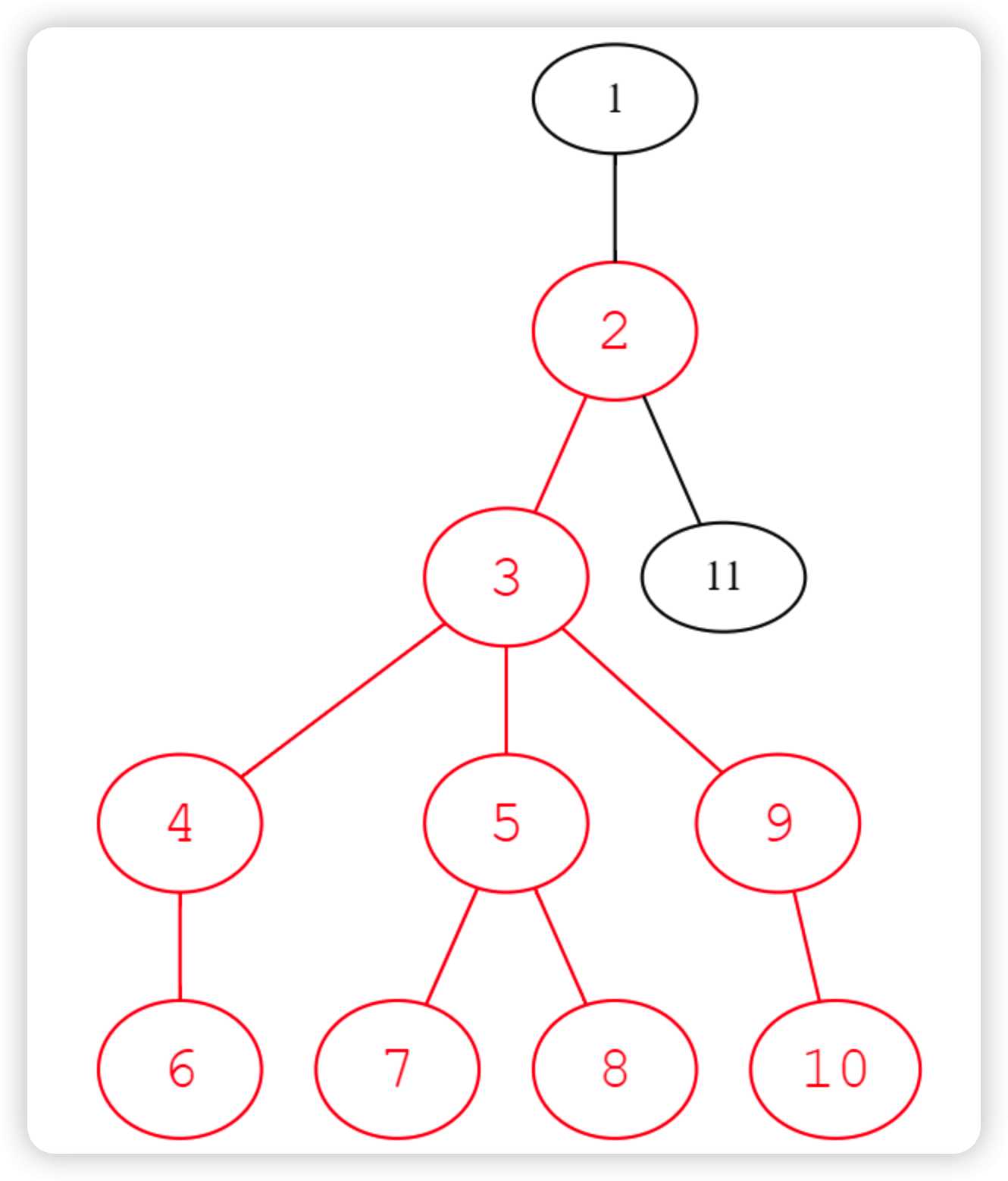
上面是头,两侧是手,中间是下体
思路:对于每一个点进行当图中的u=3进行判断,遍历每一个子结点v,如果v没有子结点,说明只能当头;如果只有一个子结点,说明能当头/手;如果有多个子结点,那么可以当头/手/下体,并且记录有多少个,放入map中,分别记录为r1,r2,r3。
然后开始枚举情况,主要注意如果手是由r3构成的,这个时候需要去枚举哪两个即可,注意不能重复。
代码:寄
1002.Independent Feedback Vertex Set(思维)
题意:给你一张特殊的图,你需要将这n个点分为两个集合s1,s2,s1中为独立集合,所有的点不能有边相连;s2中的点不能有环,只能是森林(树个数>=1),每个点都有权值,求s1的最大权值和。
首先给一个三元环(如下图左),然后每次输入两个数,代表第i+3的连接的两个点,例如1 2:

4连接1,2两条边
思路:我们可以发现,对于每一个三元环来说这三者都不能同时在集合s1中,并且有且只有一个能够在其中。所以我对其进行分类/染色,一开始的三个点分别为1,2,3颜色/类型,用num[i]来表示每个颜色代表的集合s1的权值和。
如何理解?就是说我一共分为三种情况:1拿出去做s1中,2拿出去做s1中,3拿出去做s1中,只不过我这里全部同时处理了。
为什么能够同时处理?因为每次新加入进来的点,它进入的集合是唯一的,例如上图的4,它要想进入集合s1中不能与1,2同时进,所以只能与3进,所以他是与3同一个集合的。
那么这样下来就确定了,我只要最后比较三个的权值和即可。
代码:
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
type[1] = 1, type[2] = 2, type[3] = 3;
num[1] = a[1], num[2] = a[2], num[3] = a[3];
for (int i=4;i<=n;i++)
{
cin>>u>>v;
type[i] = 6 - type[u] - type[v];
num[type[i]] += a[i];
}
cout<<max({num[1],num[2],num[3]})<<endl;
}
👍