欧氏距离
就是平常接触的最多的两点间的距离
$$
dis \ = \ \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}
$$
曼哈顿距离
曼哈顿距离其实就是美国纽约曼哈顿这个地方规划十分规整,跟巴塞罗那一样方方正正的。如图:

美国纽约曼哈顿(图源百度)
然后就类似于下方的图,就每次只能横着走或者竖着走,不能像欧氏距离可以直接斜着走,所以这个的路线可以等价于红色路线,所以距离也就是
$$
dis \ = \ |x_1-x_2| + |y_1-y_2|
$$
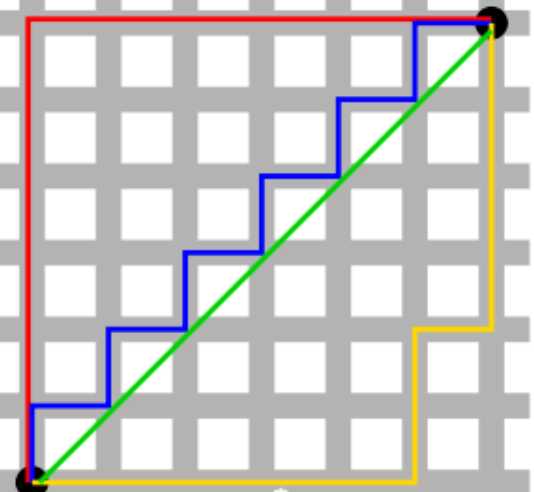
绿线就是欧氏距离,蓝线就是曼哈顿距离,黄线和红线则是另一种距离相等的曼哈顿距离
切比雪夫距离
直观理解就是国际象棋里面的国王,也就是只能往四面八方的八个方向移动一个单位。
$$
dis \ =\ max\lbrace |x_1-x_2|,|y_1-y_2| \rbrace
$$
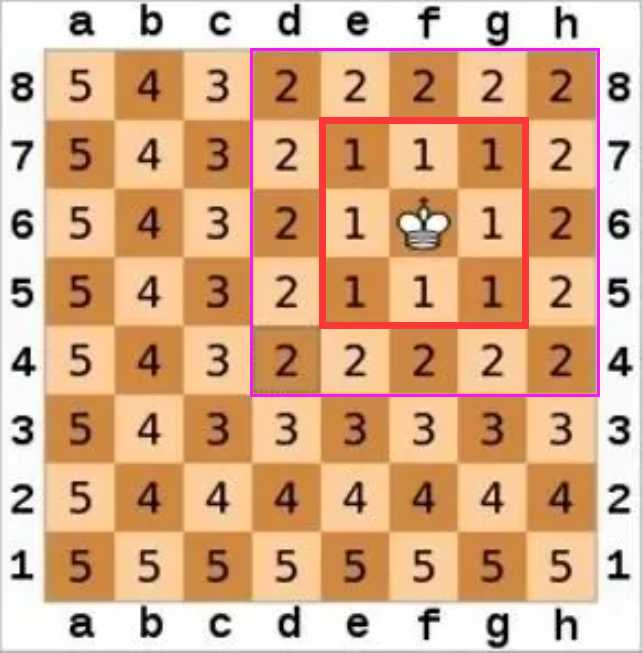
如图就是切比雪夫距离
一张图总结
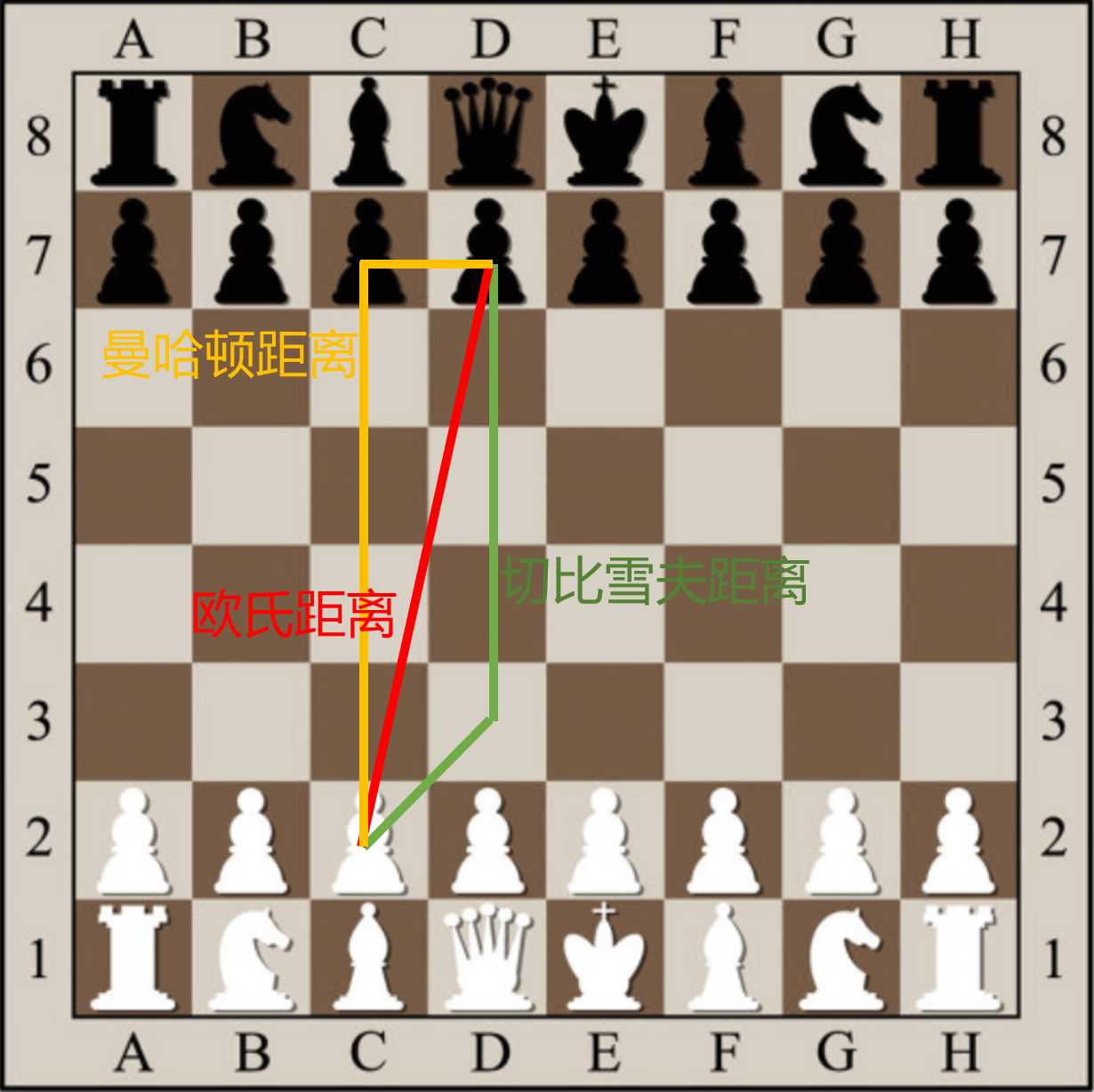
红色:欧拉距离;
黄色:曼哈顿距离;
绿色:切比雪夫距离
曼哈顿距离转切比雪夫距离(45°旋转)
这个也叫45 degree rotate。具体转换如下:
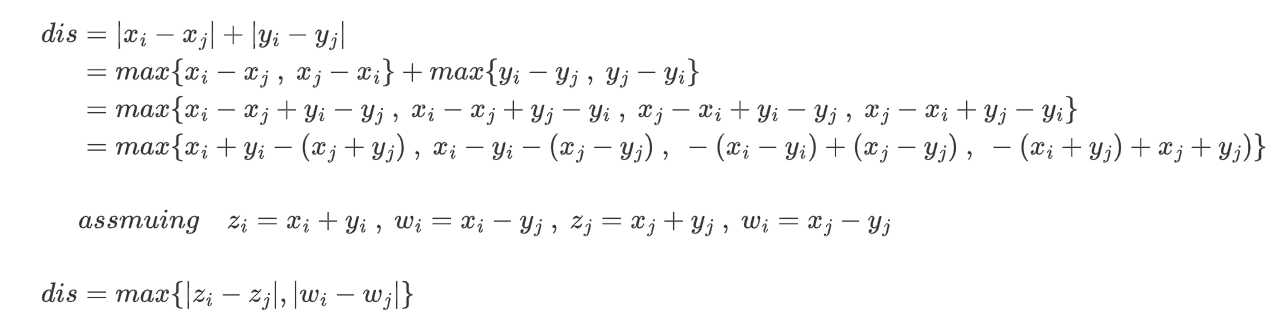
曼哈顿距离转切比雪夫距离(45°旋转)
也可以这么转换,曼哈顿距离是一个斜着45°的正方形,先将其旋转45°摆正,然后扩大$\sqrt{2}$倍。
例如下图的曼哈顿距离为$2$的区域,我将其摆正之后乘以$\sqrt{2}$就得到了红色的切比雪夫距离为$2$的区域。
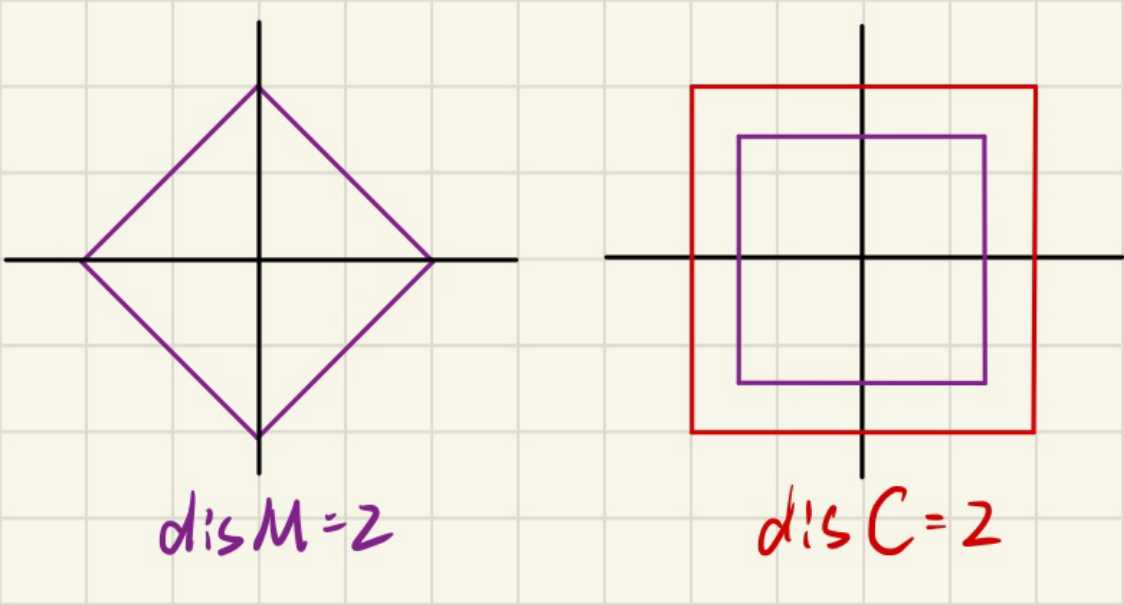
曼哈顿距离转切比雪夫距离(45°旋转)
- 曼哈顿距离转化为切比雪夫距离
在曼哈顿距离的正方形上的四条边的点$A(x,y)$的坐标旋转后变成了$(x\cdot cos\frac{\pi}{4}-y\cdot sin\frac{\pi}{4}\ ,\ y\cdot cos\frac{\pi}{4}+x\cdot sin\frac{\pi}{4})$,扩大$\sqrt{2}$倍变成了$A^\prime (\sqrt{2}(x\cdot cos\frac{\pi}{4}-y\cdot sin\frac{\pi}{4})\ ,\ \sqrt{2}(y\cdot cos\frac{\pi}{4}+x\cdot sin\frac{\pi}{4})) \Rightarrow A^\prime (x-y,x+y)$,如果是顺时针旋转则得到的是$A^\prime (x+y,x-y)$
$$
M:A(x,y)\Rightarrow C:A^\prime (x-y,x+y)
$$
- 切比雪夫距离转化为曼哈顿距离
$$
C:A(x,y)\Rightarrow M:A^\prime (\frac{x+y}{2},\frac{x-y}{2})
$$
如图:
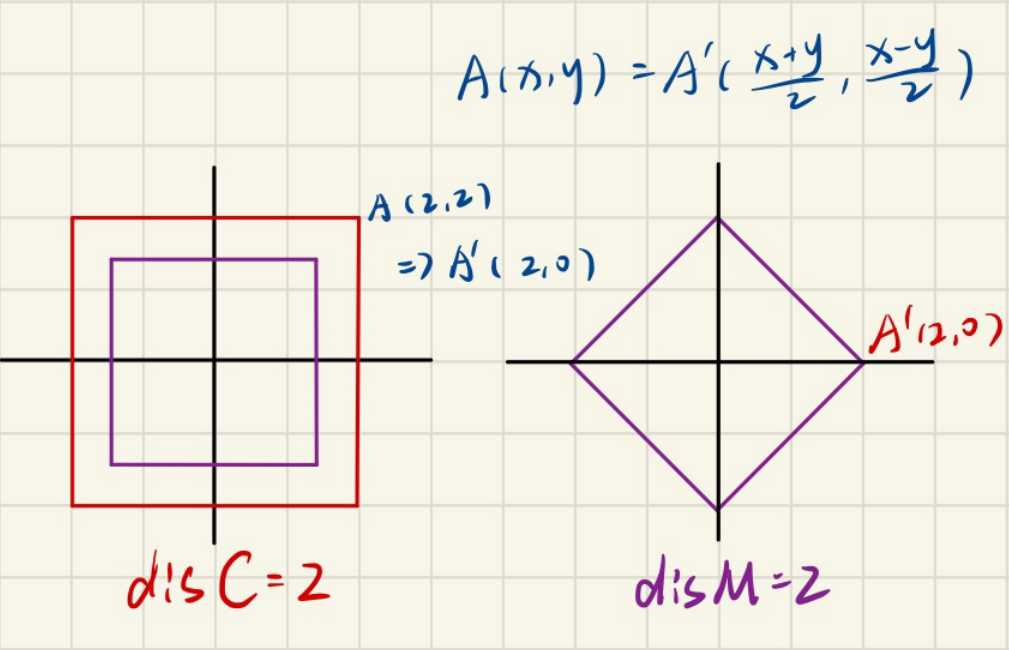
切比雪夫距离转曼哈顿距离
例题:ABC178E(求平面最远曼哈顿距离)
题目链接:E - Dist Max (atcoder.jp)
