Abstract
2DGS肯定是在3DGS出来之后的结果,3DGS虽然能高质量合成新视角并且速度快,但3D Gaussian在不同视角下的几何表现不一致,特别是对于薄物体的表面拟合不准确。
本文提出来2DGS:
- 把3D Gaussian压扁为2D 平面高斯盘(2D oriented planar Gaussian disks)
- 提供视角一致的几何,天然地建模表面
在细节方面
- 使用光线和高斯盘相交+光栅化的精确几何采样
- 引入深度畸变约束和法线一致性约束,保证薄物体和复杂结构重建稳定
最后可以在和3DGS相似的外观质量与实时渲染速度的同时,得到无噪声的几何重建

(a) 2D disks as surface elements
这些彩色的盘(disk color)和法线盘(disk normal)表示优化后的 2D 定向高斯盘,它们直接贴在真实物体表面。它们的法线方向与表面一致,这样在不同视角渲染时几何不会变形。
(b) 2D Gaussian splatting
通过 2DGS 渲染,可以得到辐射场(Radiance field)、一致的法线图(Surface normal)和深度图。法线和深度的一致性意味着无论从哪个相机视角渲染,几何形状都保持稳定。
(c) Meshing
从这些2D盘推倒出来的几何信息,可以生成无噪声且细节丰富的Mesh
📌Gaussian VS Disk
3D Gaussian是有体积的椭球,而2DGS里面的Gaussian被限制在一个平面disk上,而这个disk严格对齐到表面法线,所以它天然就是表面的一部分。
📌深度图 VS 法线图
深度图:每个像素存储相机到表面的距离
在2DGS渲染中,这个深度值是通过光线与disk相交得到的,而不是3DGS那样alpha累积间接推导的。可以直接用于几何重建Meshing
法线图:每个像素存储该像素对应表面的法线方向
每个像素
(x,y,z)存储的是(nx,ny,nz),然后将其转化成(R,G,B)在图中显示,也就是不同于灰度图,每个像素还是对应三个值RGB,只不过这里是R对应nx、G对应ny、B对应nz。看上去是彩色的,但背后是几何信息。
1. Introduction
背景:
NVS(新视角合成)和精确几何重建是CG和CV的核心任务。3DGS在渲染速度和画质上很强,但3D Gaussian没有直接约束在表面上,几何形状可能不准。
早期的surfels(surface elements,表面元素)方法很好地贴合表面,但通常需要GT、深度传感器等。
而这篇论文使用2D Gaussian盘来表示3D场景,每个盘都有方向(法线)。优点在于比3D Gaussian更能保证几何精度,因为直接建模表面没有体积。渲染的时候用ray-splat intersection,保证透视正确
使用了两个正则化项:
- Depth distortion term:约束2D Gaussian的深度分布,让它们沿射线集中在很小的范围,减少深度漂移。实际上在之前的论文里面也有,就是在一条线上可能有很多的过于分散的2D圆盘,强制它们“聚集”在一起,形成一耳光清洗的薄表面。
- Normal consitency term:让渲染出的法线和深度梯度一致,保证几何的光滑和一致性
Contribution:
- 提出了可微的2D Gaussian渲染器(支持透视正确的splatting)
- 加入两个正则化提升几何精度与光滑度
- 在几何重建和NVS上达到SOTA
.png)
3DGS已经很熟悉了,2D Gaussian其实就是一个钟型,如上图,并且是一个开放的。这里的disk并不是指2D Gaussian本身是平的,而是指它定义在一个二维平面上,这个平面作为基底,Z方向是高斯值。换句话说disk就是高斯分布的支撑域,高斯曲面就是钟型函数。它并不是像3D Gaussian那样在所有方向上都有扩展。
2. Related work
2.1 新视角合成(Novel view synthesis, NVS)
里程碑的NeRF,NeRF使用一个简单的神经网络(MLP)来学习一个连续的场景表示,Mip-NeRF解决了抗锯齿的问题,另一些工作引入了特征网络登记书。最近SIGGRAPH2023的3DGS则是一个颠覆性的工作,放弃了MLP而是使用显示的点云(高斯球)来表示,实现了实时的高质量渲染,是当前NVS的SOTA
2.2 3D重建
这任务的核心就是获得精确的几何模型,如Mesh。传统的方法如MVS(Multi-view Stereo)依赖于特征匹配和深度图融合,流程复杂。后来基于神经网络的隐式曲面表示方法(Neus,VolSDF)出现,他们学习SDF可以从中学习非常精细的表面。但是训练极其耗时间。那么这个痛点就是,精度和速度不好把控
2.3 与同期工作的对比
SuGaR让3D高斯球变得扁平,并向假象的表面对齐,2DGS不同的地方在于它的出发点更直接、更彻底,它不使用3D去模拟2D表面,而是纯粹用2D的高斯圆盘来作为基本单元。
而NeuSG是一种混合的方法。它同时优化一个3DGS模型和一个隐式的SDF网络,类似于NeuS。3DGS负责提供高校的渲染和一些几何先验,最后高质量的表面模型是从隐式SDF网络中提取的。2DGS坚持纯粹显示表示,即只用2D高斯圆盘来近似表面,没有引入额外的隐式网络。简单更快
3. 3DGS
这篇在20250605-3DGS论文分享中详细介绍了。要引入2DGS,那么说3DGS肯定有地方不好,问题在于
- 3D Gaussian本质是有体积的,而真实世界物体表面是薄的,用有厚度的去模拟纸这是不显示的
- 3D Gaussian并没有法线信息。
- 缺乏多视角一致性。对于同一个三维点,不同视角渲染出来的深度值可能是不一致的。
- 投影的透视不准确,3DGS是一个仿射变换的近似,只在中心点附近比较准确。
4. 2DGS
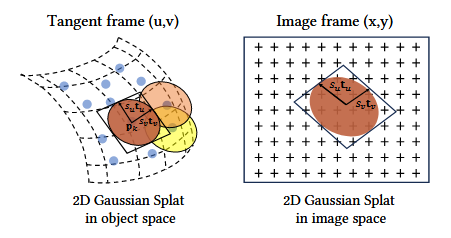
4.1 建模(Modeling)
核心思想:放弃3DGS三维blob,而是用扁平的2D圆盘嵌入在三维空间中
3D高斯球是由一个三维协方差矩阵来定义的,而2D高斯圆盘则由一组更直观的几何参数来定义:
- 中心点
p_k,就是中心坐标 - 两个主切线向量(
t_u,t_v):这两个互相正交的向量定义了圆盘所在的平面,局部坐标系的u,v轴 - 一个缩放向量(
S=(s_u,s_v)):这两个数值分别控制圆盘沿着t_u,t_v轴“半径”的大小,所以这可能是椭圆形也可能是正圆形。 - 外观属性:也有不透明度
\alpha和颜色c
有了这些之后,我们很容易能够得到法线,那么就是t_w=t_u\times t_v,只要模型学会了正确的朝向t_u,t_v就会学会表面的法线方向。
公式(4)和公式(5)讲述了从局部坐标到世界坐标
P(u,v)=\mathrm{p}_k+s_u\mathrm{t}_uu+s_v\mathrm{t}_vv=\mathbf{H}(u,v,1,1)^\mathrm{T}\tag{4}这个公式解释的是,在圆盘局部切空间下的二维坐标,从中心点p_k出发,沿着缩放后的t_u走u个单位,然后沿着t_v走v个单位。
公式(5)讲的是图形学中齐次坐标,将上述过程写成了矩阵的形式。这个H是标准的变换矩阵,它将圆盘的缩放、旋转和平移信息全部整合在一起,可以直接将局部的二维点(u,v,1,1)^T变换到三维世界坐标系中,这在GPU上并行计算非常高效。
高斯公式定义,公式(6)
\mathcal{G}(u)=\exp(-\dfrac{u^2+v^2}{2})边缘柔和的软圆盘,颜色和不透明度在中心点最强,然后向四周平滑地衰减。
这里举一个例子,2D高斯圆盘比作一张纸,在空间中某个位置,现在要表示这张纸的
(10,5)的位置在空间中是多少,那么它的坐标系就是长宽方向的t_u,t_v,第一感觉是p=p_k+10\times t_u+5\times t_v,但是这个(10,5)是在纸上的度量,在纸上说的10也许就是10mm,但是在我们三维坐标系中一般说的是1m,所以还需要乘以缩放。
4.2 Splatting
如何高效且住求虐地把这些三维空间中的圆盘绘制到二维图像上?
3DGS那样直接用一个仿射变换,把2D圆盘投影到图像上。缺陷是仿射变换无法完全模拟真实的透视投影(近大远小),这种近似只在圆盘中心点附近是准确的,离中心越远,几何畸变就越严重。
之前有些方法为了精确实现透视投影,需要计算一个变换矩阵的逆矩阵M=(WH)^{-1},在圆盘被侧着看(退化成线)的时候,这个矩阵会变得奇异或接近奇异,求逆运算数值不稳定。
那么2DGS的巧妙解法是:光线-圆盘精确求交(Ray-splat Intersection)
把问题反过来看,并不是在问“一个三维圆盘投影到图像是什么形状”,而是在问“屏幕上任意一个像素发出的光线,会射中三维圆盘的哪个位置?”
-
用两个平面定义一条光线。一条直线,看作是两个平面的交线,例如对于屏幕像素
(x,y)它发出的光线可以被定义为x坐标平面和y坐标平面的交线。x-plane等同于x坐标等于x的平面,它的法向量是(-1,0,0),偏移量是x,所以这个平面的四维向量可以表示为h_x=(-1,0,0,x)^T,同理y-plane就是h_y=(0,-1,0,y)^{T},满足这两个平面上的点,就一定在这条光线上。 -
变换平面,而非求逆。求交点传统方法可能复杂,但这里用齐次坐标的一个优美特性:用矩阵M变换平面上的点,等价于用M的逆转置矩阵
M^{(-T)}来变换这个平面的方程参数。
世界坐标系变换到圆盘局部uv坐标系的变换矩阵是M=(WH)^{-1},那么用来变换平面h_u,h_v的矩阵就是(M)^{-T}=((WH)^{-1})^{-T}=(MH)^T -
高效求交:当光线平面被变换到圆盘局部的
(u,v)坐标系后,求交点就是一个非常简单二元一次方程组
\mathbf{h}_u\cdot (u,v,1,1)^\mathrm{T}=\mathbf{h}_v\cdot (u,v,1,1)^\mathrm{T}=0\tag{9}这个方程是有解析解的:
u(\mathbf{x})=\frac{\mathbf{h}_{u}^{2}\mathbf{h}_{v}^{4}-\mathbf{h}_{u}^{4}\mathbf{h}_{v}^{2}}{\mathbf{h}_{u}^{1}\mathbf{h}_{v}^{2}-\mathbf{h}_{u}^{2}\mathbf{h}_{v}^{1}}\qquad v(\mathbf{x})=\frac{\mathbf{h}_{u}^{4}\mathbf{h}_{v}^{1}-\mathbf{h}_{u}^{1}\mathbf{h}_{v}^{4}}{\mathbf{h}_{u}^{1}\mathbf{h}_{v}^{2}-\mathbf{h}_{u}^{2}\mathbf{h}_{v}^{1}}\tag{10}这样就求出来光线与圆盘相交的局部坐标系(u(x), v(x))
特殊情况:退化解。当圆盘被侧着看的时候,即使求交是稳定的,但是在屏幕的投影可能非常细,甚至细到无法覆盖任何一个像素中心,解决方案是引入了一个”低通滤波器“作为保底项,最终的高斯贡献值\hat{\mathcal{G}}(x)取精确求交计算出的高斯值和一个以圆盘投影中心c为中心、固定大小\sigma的屏幕空间高斯值的最大值。
\hat{\mathcal{G}}(x)=\max\{\mathcal{G}(u(\mathbf{x})), \mathcal{G}(\dfrac{\mathbf{x}-\mathbf{c}}{\sigma}\}- 如果是退化成线的时候,前者会趋近于0,这样会导致没有梯度基本上没有贡献,也无法修正参数。
- 后者的
\mathbf{c}就是这个圆盘的中心坐标,\mathbf{x}就是当前像素的坐标,这个式子在屏幕空间创建了一个以\mathbf{c}为中心,半径为\sigma的高斯光斑
最后就是光栅化,和3DGS非常相似
\mathbf{c}(\mathbf{x})=\sum_{i=1}\mathbf{c}_{i}\alpha_{i}\widehat{\theta}_{i}(\mathbf{u}(\mathbf{x}))\prod_{j=1}^{i-1}(1-\alpha_{j}\widehat{\theta}_{j}(\mathbf{u}(\mathbf{x})))\tag{12}这里有些云里雾里的
-
H矩阵是什么?
这是每个2D高斯圆盘自己独有的,有N个圆盘就有N个不同的矩阵。我们通过这个把局部二维坐标系
(u,v)放到宏观的三维世界坐标系上。 -
W矩阵是什么?
这个矩阵对于某一帧来说是唯一的,它表示的相机的位置和朝向,视图矩阵。作用是把三维世界坐标系里面所有点都转换到以相机为原点的坐标系中去,在这个坐标系中相机通常位于
(0,0,0),看向Z轴的负方向。
那么现在给我的第一反应是,对于每一个像素都有一个射线打出,沿路积分对每个路径上的高斯圆盘计算贡献,通过求交来然后得到最后的颜色。我们计算的(u,v)本身是没有颜色的,不是纹理贴图那样的,而是代入高斯公式里面计算一个权重,越远当然越小。但是这里有优化的地方,就是遍历高斯圆盘,可以计算出它大致影响哪些像素点,可以计算出一个屏幕上完全包住的矩形包围盒。
5 训练
核心问题:如果只依靠“光度损失”(Photometric Loss),也就是只让渲染出来的图片和训练照片长得像,那么重建出的几何模型将会是充满噪声的。
为什么会这样?
想象一下,一条光线穿过空间。你可以用一片不透明度为 1 的圆盘来挡住它,也可以用两片不透明度为 0.5 的、在光线上前后错开的圆盘来叠加。对于相机来说,最终看到的颜色和深度可能非常相似。这就给了优化器“偷懒”的空间,它会满足于生成一团松散的、而非紧凑的表面。
- 深度扭曲损失,
\mathcal{L}_d
目标:让贡献同一个像素颜色的所有圆盘,在深度上(也就是沿着光线方向)紧紧地“贴”在一起。
\mathcal{L}_{d}=\sum_{i,j}\omega_{i}\omega_{j}|z_{i}-z_{j}|\tag{13}i,j表示两个不同的圆盘z_i,z_j表示两个圆盘与光线交点的深度值,上面描述的是绝对距离\omega_i,\omega_j这是贡献权重,越不透明、交点越靠近它的中心,权重就越大- 整体来说这个计算了光盘两两之间的加权距离,例如有三个圆盘5.0,5.2,5.8,可能加了损失之后变成了5.1,5.11,5.12。
- 法线一致性损失,
\mathcal{L}_n
\mathcal{L}_{n}=\sum_{i}\omega_{i}(1-\mathbf{n}_{i}^{\top}\mathbf{N})\tag{14}目标:让每一个 2D 圆盘自身的朝向,与它所在的、由深度图推算出的宏观表面朝向保持一致
n_i就是自身的法线,也就是t_u,t_v向量叉乘得到的。N是深度图计算出来的表面法线,公式(15)表示它是通过计算一个点与邻近点的位置,然后用法向量计算方法(有限差分)得到的。
\mathbf{N}(x,y)=\frac{\nabla_{x}\mathbf{p}_{s}\times\nabla_{y}\mathbf{p}_{s}}{|\nabla_{x}\mathbf{p}_{s}\times\nabla_{y}\mathbf{p}_{s}|}\tag{15}那么最后就是三者的集中,最主要的\mathcal{L}_c就是光度损失,肯定得保证外观上逼近真实照片
\mathcal{L}=\mathcal{L}_{c}+\alpha\mathcal{L}_{d}+\beta\mathcal{L}_{n}6 实验
6.1 网格提取 Mesh Extraction
它们采样的不是直接把上百万个椭圆盘片三角花,而是一个更经典且鲁棒的简介流程:
-
训练好的2DGS模型生成高质量的深度图(Depth Maps)
选择那些相机视角,为每一个视角都渲染出一个深度图,这里的深度值就是法线损失光路累计不透明度达到0.5那个点的深度,这被认为是表面的位置。
深度图:对于一个图形学普通里面的,那么光线打过去碰到的第一个交点与相机的距离当然就是深度值。但是在3DGS/2DGS里面并不是真实的物体,而是一个个高斯盘,每个盘都有一个不透明度来做出贡献,那么我们规定不透明度达到0.5的这个才是表面。
通过深度图之后,我们可以计算出宏观法线
N,通过公式(15)一个店和它周围点的三维坐标来计算法线。 -
使用TSDF Fusion融合多视角深度图
TSDF(Truncated Signed Distance Function, 截断符号距离函数)在三维重建中是一个非常经典的技术。在三维空间中建立一个精细的体素网格。网格中每个体素都存储一个值,表示这个方块的中心到最近的物体表面的距离,有正有负,外部就是正,内部就是负
Fusion(融合)的过程就是把第一步各个角度渲染出来的深度图,一张张地去更小每个小方块的TSDF值,多个视角的信息会相互补充和修正,最后就是一个描述准确的表面
-
使用Marching Cubes算法提取三角网格
算法找到所有TSDF值为0的地方(也就是物体表面所在的位置),并根据这些位置生成最终的三角网格(Mesh)
在学习TSDF算法的时候,我在想一个体素上存储的值类似于SDF的,是用体素到相机的距离减去表面到相机的距离,那么我既然都知道表面到相机的距离还用这个干什么呢?实际上深度相机我们是知道d_{\mathrm{surface}}的,每一帧中每一个像素都有一个深度值,就是相机到该像素处物体表面的距离,这是知道的。
所以对于体素中心X,我们将其转化成相机坐标系中,投影到像素平面得到(u,v)可以求出此时的深度值d(u,v),这就是d_{\mathrm{surface}},做差就可以得到TSDF
