19年牛客多校8——CDMA（递归）

题意

给你一个$m$($m\in \lbrace 2^k | k=1,2,...,10\rbrace $)，你需要构造一个$m\times m$的矩阵，要求任意两行的内积为$0$，内积也叫点积：对于$a,b$有$a\cdot b=\sum _{i=1}^{n}a_ib_i=a_1b_1+a_2b_2+\cdots +a_nb_n$

思路

构造，当$n=2$的时候，我们构造出

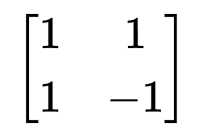
嗯，然后按照下面方法构造，我问大佬们为什么，感觉是对的，他们说“瞎**构造”就好

就是每个这样的小块往其他方向填：

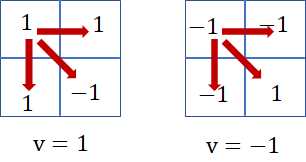
每次递归，有一个$v$，要么是$1$，要么是$-1$，然后往其他地方填

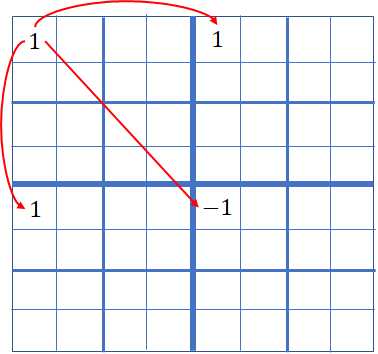
然后这个时候，相当于又是矩阵的开始，这回是$4$个$4\times 4$小矩阵，然后继续往下dfs

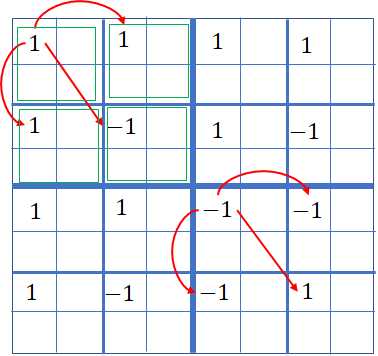
然后继续往下传递，继续分成若干个$2\times 2$的矩阵，直到$n=1$的时候填入当前的$v$

如何理解$v$？
这个$v$就是我们之后要填入数字的数，但是会一直变化，比如$-1\times (-1)=1$，这个时候又是$1$了，
正如上图右下角，这整块的$v$ 是-1，但是会随着之后的变化可能会改变，比如最后一个变成了1

如何理解可行性？
我的理解是整体都满足，一开始从小的$2\times 2$的矩阵慢慢变大，同样满足，实际上我们能看出，大的矩阵的$v$进行内积计算还是$0$，所以一直满足

代码

inline void dfs(int i,int j,int n,int v)
{
    if (n==1) {a[i][j]=v;return;}
    dfs(i,j,n/2,v);
    dfs(i+n/2,j,n/2,v);
    dfs(i,j+n/2,n/2,v);
    dfs(i+n/2,j+n/2,n/2,-v);
}

inline void Case_Test()
{
    cin>>n;
    dfs(1,1,n,1);
    rep(i,1,n) rep(j,1,n) cout<<a[i][j]<<" \n"[j==n];
}