02-凸集
向量范数
范数(Norm) 是一种用于衡量向量或矩阵大小的数学函数。简单来说,范数可以理解为表示“距离”或“长度”的概念,用于评估向量或矩阵的大小或规模。
定义:
令记号
\Vert \cdot \Vert: \mathbb{R}^n\rightarrow\mathbb{R}^+是一种非负函数,满足:
- 正定性:
\Vert v\Vert\geq0- 齐次性:
\Vert \alpha v\Vert =|\alpha|\Vert v\Vert- 三角不等式:
\Vert v+w\Vert \leq \Vert v\Vert +\Vert w\Vert
最常用的向量范数即是我们熟知的\ell_p范数,且p\geq 1
\Vert v\Vert_p=\Bigg(\sum_{i=1}^{n}|v_i|^p\Bigg)^{\frac{1}{p}};
柯西不等式:|a^Tb|\leq \Vert a\Vert_2 \Vert b\Vert_2,等号成立是a和b线性相关。
矩阵范数
矩阵范数由向量范数推广得到的,
\Vert A\Vert_1=\sum_{i,j}|A_{ij}|\Vert A\Vert_F=\sqrt{\sum_{i,j}A_{ij}^2}=\sqrt{\mathbf{Tr}(AA^T)}
“谱”其实是关于矩阵的特征值,矩阵的二范数不是所有元素平方(F-范数)
\Vert A\Vert_{p=2}=\max_{\Vert x\Vert_2=1}\Vert Ax\Vert_2=\sqrt{\lambda_\max(A^TA)}
1-范数是竖着的,所以是列和的最大值
\infty范数是横着的,所以是行和的最大值
- 核范数定义:
\Vert A\Vert _*=\sum_{i=1}^{r}\sigma_i
也就是所有非零奇异值的和,r=\mathbf{rank}(A)
- 矩阵A,B的内积定义为:
\langle A, B \rangle = \text{Tr} (A B^\top) = \sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij} b_{ij}
- 柯西不等式,设
A,B\in \mathbb{R}^{m\times n}
|\langle A, B\rangle |\leq \Vert A\Vert_F\Vert B\Vert_F
等号成立当且仅当A和B线性相关
凸集的定义
在\mathbb{R}^n空间中,经过不同的两点x_1,x_2可以确定一条直线,方程为:
y=\theta x_1+(1-\theta)x_2,\theta\in\mathbb{R}
特别的,当\theta\in[0,1]的时候是线段,如下:
-
仿射集
若过集合
\mathcal{S}中的任意两点的直线都在\mathcal{S}内,则称\mathcal{S}为仿射集即:
x_1,x_2\in\mathcal{S}\Rightarrow \theta x_1+(1-\theta)x_2\in\mathcal{S},\forall \theta \in \mathbb{R}
线性方程组
Ax=b的解集\mathcal{X}是仿射集因为
\forall x_1,x_2\in\mathcal{X}(x_1\neq x_2)均满足\theta Ax_1+(1-\theta)Ax_2=b
-
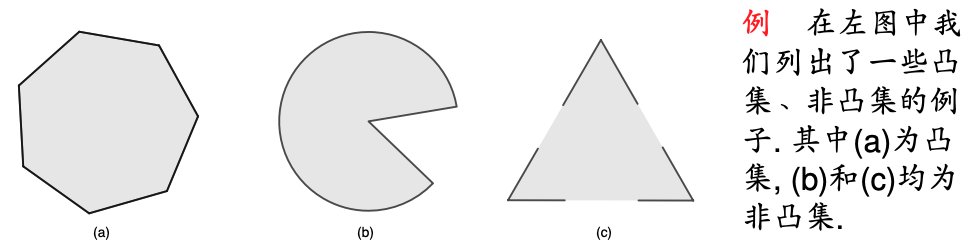
凸集
如果连接集合
\mathcal{S}的任意两点的线段都在\mathcal{S}内,则称S为凸集,即
x_1,x_2\in\mathcal{S}\Rightarrow \theta x_1+(1-\theta)x_2\in\mathcal{S},\forall \theta\in[0,1]
仿射集当然都是凸集
-
凸集的性质:
定理(若
\mathcal{S},\mathcal{T}都是凸集):k\mathcal{S}=\{ks\mid k\in\mathbb{R},s\in \mathcal{S}\}也是凸集\mathcal{S+T}=\{s+t\mid s\in\mathcal{S},t\in \mathcal{T}\}也是凸集\mathcal{S}\cap\mathcal{T}也是凸集- 凸集的内部和闭包都是凸集
-
凸组合
形如:
x=\theta_1 x_1+\theta_2x_2+\cdots +\theta_kx_k,\\\theta_1+\cdots+\theta_k=1,{\color{red}\theta_i\geq 0},i=1,\cdots,k.
\\ \text{的点称为}x_1,\cdots,x_k\text{的凸组合}
凸组合知识在凸集中选择特定点进行线性组合得到的点,因此它是凸集的子集。
点集的凸包等价于该点集的所有凸组合。
-
凸包:集合
\mathcal{S}的所有点的凸组合构成的点集为\mathcal{S}的凸包,记为\mathbf{conv}\mathcal{S} -
\mathbf{conv}\mathcal{S}是包含\mathcal{S}的最小凸集 -
仿射包
仿射包和凸集定义很小,
\theta的范围有所不同- 仿射组合的定义
形如:
x=\theta_1 x_1+\theta_2x_2+\cdots +\theta_kx_k,\\\theta_1+\cdots+\theta_k=1,{\color{red}\theta_i\in\mathbb{R}},i=1,\cdots,k.
\\ \text{的点称为}x_1,\cdots,x_k\text{的仿射组合}
-
仿射包
集合
\mathcal{S}的所有点的仿射组合构成的点集为\mathcal{S}的仿射包,记为\mathbf{affine}S\mathbf{affine}S是包含\mathcal{S}的最小仿射集
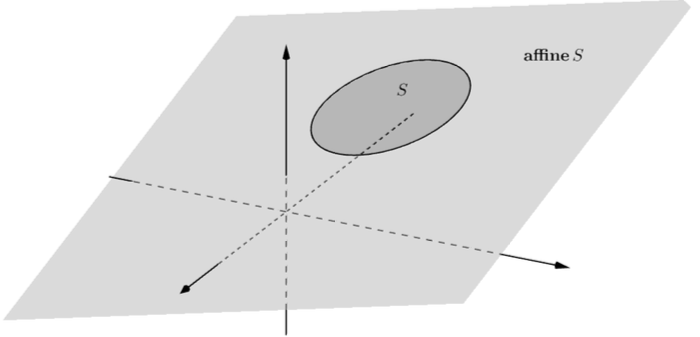
仿射包直接将原集合拓展为了其所在的全平面
-
锥组合
- 锥:对于集合
\mathcal{S}中的任意点x和任意\theta\geq0都有\theta x\in \mathcal{S}
相比于凸组合和仿射组合,锥组合不要求系数和为
1,锥组合一般都是开放的- 锥组合 形如:
- 锥:对于集合
x=\theta_1x_1+\cdots\theta_kx_k,\theta_i\geq0(i=1,\cdots,k).\\
\text{的点称为}x_1,\cdots,x_k\text{的锥组合}
- 凸锥:若集合
\mathcal{S}中的任意点的锥组合都在\mathcal{S}中,则称\mathcal{S}为凸锥 -
非凸锥的例子:坐标轴第一和第三象限的并集,
y=|x|
上图显示了二维平面包含两点x_1,x_2的凸锥,可见两点若不共线,则形成的凸锥为一个半径无穷的圆的扇形部分。
重要的凸集举例
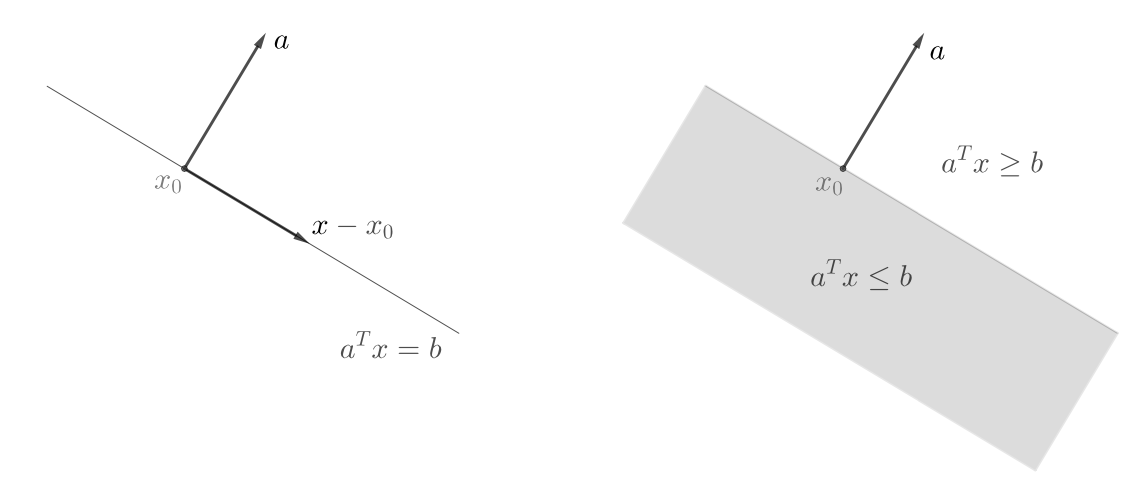
- 超平面:任取非零向量
a\in\mathbb{R}^n,形如\{a\mid a^Tx=b\}的集合称为超平面 - 半空间:任取非零向量
a\in\mathbb{R}^n,形如\{a\mid a^Tx\leq b\}的集合称为半空间
超平面是仿射集和凸集, 半空间是凸集但不是仿射集.
- 多面体:满足线性等式和不等式组的点的集合称为多面体,即
\{x\mid Ax\leq b,Cx=d\}
其中A\in \mathbb{R}^{m\times n},C\in\mathbb{R}^{p\times n},x\leq y表示向量逐元素小于。
多面体是有限个半空间和超平面的交,所以也是凸集
-
范数球
设空间中到某一定点
x_c(称为中心)的距离小于等于定制r(称为半径)的点的集合为(范数)球,即:
\mathrm{B}(x_c,r)=\{x\mid \Vert x-x_c\Vert\leq r\}=\{x_c+ru\mid \Vert u\Vert \leq 1\}
一般而言2-范数球
-
椭球
形如:
\{x\mid (x-x_c)^TP^{-1}(x-x_c)\leq 1\}=\{x_c+Au\mid \Vert u\Vert_2\leq 1\}
的集合为椭球,x_c为椭球中心,p对称正定,且A非奇异,可以认为是球仿射变换而来(A)
-
范数锥
形如:
\{(x,t)\mid \Vert x\Vert \leq t\}
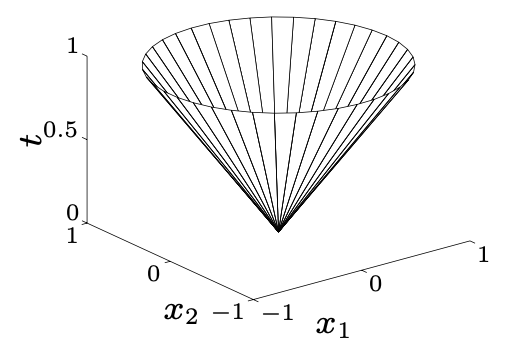
当t=0的时候,是最下面的点;当t=1的时候,是最上面的圆
-
特殊矩阵集合和(半)正定锥
(待完善)
-
半正定锥的例子:
(二阶主子式忘记了)
保凸的运算
仿射变换的保凸性
Ax=b的解集是仿射集,任何一个仿射集可以由Ax=b来表示
仿射变换的保凸性: 设f:\mathbb{R}^n\rightarrow \mathbb{R}^m是仿射变换,即f(x)=Ax+b,A\in \mathbb{R}^{m\times n},b\in\mathbb{R}^m,那么有:
- 凸集在
f下的像是凸集:\mathcal{S}\subseteq\mathbb{R}^n\text{是凸集}\Rightarrow f(\mathcal{S})=\{f(x)\mid x\in\mathcal{S}\text{是凸集}\} - 凸集在
f下的原像是凸集:\mathcal{C}\subseteq\mathbb{R}^m\text{是凸集}\Rightarrow f^{-1}(\mathcal{C})=\{f(x)\mid x\in\mathcal{C}\text{是凸集}\}
证明第一个:
\forall y_1,y_2\in f(\mathcal{S}),\exists x_1,x_2\in\mathcal{S}\\
Ax_1+b=y_1\\
Ax_2+b=y_2\\
\begin{align}
\forall \lambda\in[0,1],\quad & \quad\ \lambda y_1+(1-\lambda)y_2\in f(\mathcal{S})\\
&=\lambda(Ax_1+b)+(1-\lambda)(Ax_2+b)\\
&=A(\lambda x_1+(1-\lambda)x_2)+b\\
&\text{其中}A(\lambda x_1+(1-\lambda)x_2\in\mathcal{S}
\end{align}
例 线性矩阵不等式的解集
\{x\mid x_1A_1+\cdots +x_mA_m\preceq B\}(A_i,i=1,\cdots,m,B\in\mathcal{S}^p)是凸集,这由仿射变换可以直接得到
老师方法:
\begin{align} f(x)&=B-(x_1A_1+\cdots+x_mA_m)\\ &=B-A(x) \end{align}
x_1,x_2,\cdots,x_m不是向量是数,B是个常量,(x_1A_1+\cdots+x_mA_m)是线性变换要证明
\{x\mid B-A(x)\in\mathcal{S}_+^n\}是凸集,B-A(x)是仿射变换,\mathcal{S}_+^n是凸集
注意:
A\preceq B表示0\preceq B-A是半正定(\preceq的LaTeX为\preceq)A\prec B表示0\prec B-A是正定(\prec的LaTeX为\prec)- 线性变换:
A(x_1+x_2)=A(x_1)+A(x_2)
A(kx)=kA(x)
- 仿射变换:
线性变换+常数
(GPT椭圆和圆的关系)
例 双曲锥
\{x\mid x^TPx\leq (c^Tx)^2,c^Tx\geq 0,P\in \mathcal{S}_+^n\}是凸集
证明:双曲锥可以转化为二阶锥
二次锥:(
\{(x,t)\mid \Vert x\Vert_2\leq t,t\geq 0\})对x和t都进行仿射变换
(Ax+b,c^Tx+d)\Rightarrow \Vert Ax+b\Vert_2\leq c^Tx+d,c^Tx+d\geq 0 \\x^TPx=x^TA^TAx=\Vert Ax\Vert_2^2\leq c^Tx\{x\mid \Vert Ax\Vert_2\leq c^Tx,c^Tx\geq 0,A^TA=P\}而二阶锥可由二次锥
\{(x,t)\}\mid\Vert x\Vert)2\leq t,t\geq 0经过仿射变换得到,所以均为凸集。
- 透视变换
P:\mathbb{R}^{n+1}\rightarrow \mathbb{R}^n
P(x,t)=x/t,\quad \text{dom} P=\{(x,t)\mid t>0\}
透视变换下凸集的像和原像是凸集
- 分式线性变换
f:\mathbb{R}^n\rightarrow \mathbb{R}^m
f(x)=\dfrac{Ax+b}{c^T+d}, \quad \mathbf{dom} f=\{x\mid c^T+d\gt 0\}
分式线性变换下的凸集的像和原像是凸集,分子分母都是仿射变换
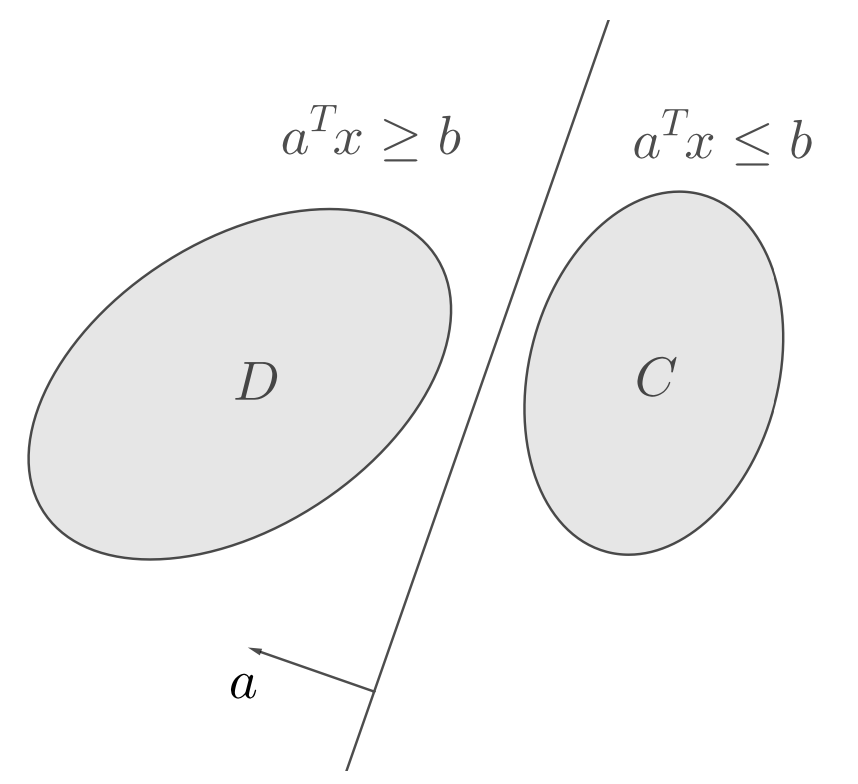
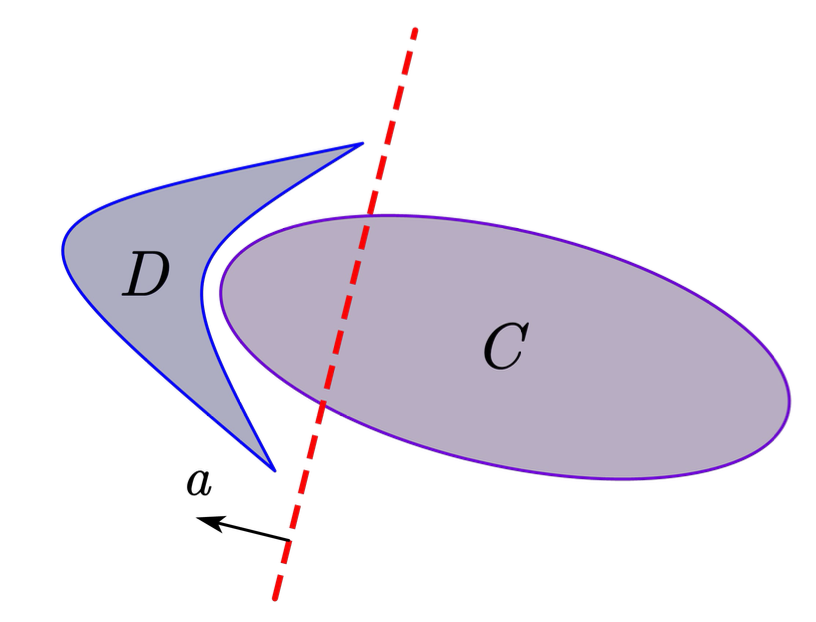
分离超平面定理
超平面是空间中一类特殊的凸集(仿射集), 可以证明\mathbb{R}^n空间中的超平面 恰好是n − 1维的. 我们可以用超平面分离不相交的凸集.
分离超平面定理:如果\mathcal{C}和\mathcal{D}是不相交的凸集,则存在非零向量a和常数b,使得
a^Tx\leq b,\forall x\in\mathcal{C},
且
a^Tx\geq b,\forall x\in\mathcal{D}
即超平面\{\mid a^Tx=b\}分离了\mathcal{C}和\mathcal{D}
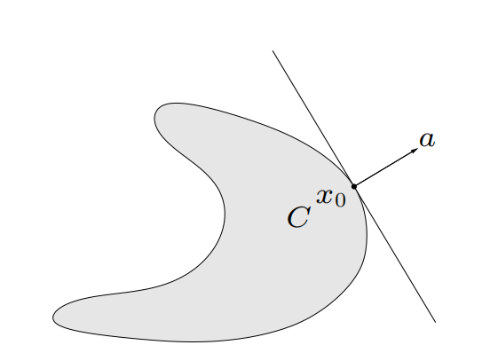
支撑超平面:
针对单个凸集来说的
给定集合\mathcal{C}以及边界上的点x_0,如果a\neq 0满足a^T\leq a^tx_0,\forall x\in\mathcal{C},那么称集合
\{x\mid a^Tx=a^Tx_0\}
为\mathcal{C}在边界点x_0的的支撑超平面
支撑超平面定理:若\mathcal{C}是凸集,则\mathcal{C}的任意边界点都存在支撑超平面: