最优化期末复习

最优化考试内容

期末考试题型

总分100，时间120min

简答题（名词解释），共5小题，每题6分，共30分

计算题，共5小题，每题10分，共50分

证明题，共2小题，每题10分，共20分

简答题

凸集、仿射集、凸锥
凸函数、凸函数的判定定理、与标量函数的复合、共轭函数
凸优化问题的标准形式、线性规划的标准形式、二次规划的标准形式、半定规划的标准形式
Armijo准则、次梯度的定义
拉格朗日函数、拉格朗日对偶函数、拉格朗日对偶问题、弱对偶原理、Slater条件与强对偶、KKT条件
交替方向乘子法适用的类型、算法步骤

计算题

课件中的例子
平时作业
- 2.6(1)和(2)，2.7,2.12(b)
- 2.13,4.1,4.3
- 6.2
- 5.7,5.10(求出KKT点),5.16

证明题

凸优化问题的可行域、解集都是凸集
弱对偶原理
Slater条件满足时，KKT条件是凸问题全局最优解的一阶充要条件
- Slater条件说明强对偶性成立，且最优化可以达到
- 必要性，充要性
交替方向乘子法的收敛性准则

简答题

凸集、仿射集、凸锥

定义：

【凸集】：如果连接集合\mathcal{S}中的任意两点的线段都在\mathcal{S}内，则称\mathcal{S}为凸集，即
x_{1},x_{2}\in S\Rightarrow\theta x_{1}+(1-\theta)x_{2}\in S,0\leqslant\forall\theta\leqslant1
【仿射集】：若过集合\mathcal{S}中的任意两点的直线都在\mathcal{S}内，则称\mathcal{S}为仿射集，即
x_{1},x_{2}\in S\Rightarrow\theta x_{1}+(1-\theta)x_{2}\in S,\forall\theta\in\mathbb{R}.
锥：对于集合\mathcal{S}中的任意点x和任意\theta\geq 0都有\theta x\in \mathcal{S}.

锥组合：形如
x=\theta_{1}x_{1}+\cdot\cdot\cdot+\theta_{k}x_{k},\theta_{i}\geqslant0~(i=1,\cdot\cdot\cdot\cdot,k).
的点称为x_1,\cdots, x_k的锥组合.

【凸锥】：若集合\mathcal{S}中任意点的锥组合都在\mathcal{S}中，则称\mathcal{S}为凸锥.

凸函数、凸函数的判定定理、与标量函数的复合、共轭函数

【凸函数定义】：

函数f:\mathbb{R}^{n}\to\mathbb{R}，若\mathrm{dom}f是凸集，且
f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y)
对所有x,y\in\mathsf{d o m}f~,0\le\theta\le1都成立，则称f是凸函数

【凸函数的判定定理】：

f:\mathbb{R}^{n}\to\mathbb{R}是凸函数，当且仅当对每个x\in\mathsf{d o m}f,v\in\mathbb{R}^{n}，函数g:\mathbb{R}\to\mathbb{R}是关于t的凸函数
g(t)=f(x+t\nu),\quad\mathrm{dom}~g=\{t|x+t\nu\in\mathrm{dom}f\}

【与标量函数的复合】:

给定函数g: \mathbb{R}^n\rightarrow \mathbb{R}和h:\mathbb{R}\rightarrow \mathbb{R}，


f(x)=h(g(x))

若

g是凸函数，h是凸函数，\tilde{h}单调不减
g是凹函数，h是凸函数，\tilde{h}单调不增

那么f是凸函数

对于n=1，g,h都可微分的情况，给出简证


f^{\prime\prime}(x)=h^{\prime\prime}(g(x))g^\prime(x)^2+h^\prime(g(x))g^{\prime\prime}(x).

要使得f^{\prime\prime}(x)\geq 0，那么需要每一项都大于等于，充分条件为：

h^{\prime\prime}(g(x))\geq 0,h^\prime(g(x))\geq 0,g^{\prime\prime}(x)\geq 0
h^{\prime\prime}(g(x))\geq 0,h^\prime(g(x))\leq 0,g^{\prime\prime}(x)\leq 0

那么则分别对应两种情况

h为凸函数，h不递减，g为凸函数
h为凸函数，h不递增，g为凹函数

g,h不可微分的时候，结论依然成立

推论：

如果g是凸函数，则\exp g(x)是凸函数
如果g是正值凹函数，则1/g(x)是凸函数（这里用第二条规则）

【共轭函数】

函数f的共轭函数定义为


f^{*}(y)=\operatorname*{sup}_{x\in\mathrm{dom}f}(y^\mathsf{T}x-f(x))

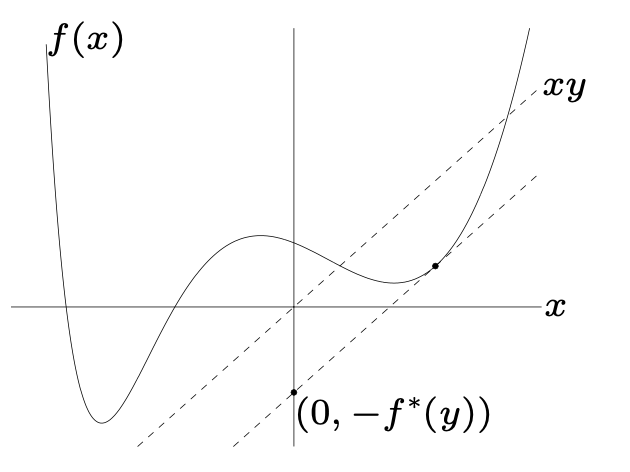
例子：f(x)=-\log x和f(x)=(1/2)x^{T}Q x,~Q\in\mathbb{S}_{++}^{n}

凸优化问题的标准形式、线性规划的标准形式、二次规划的标准形式、半定规划的标准形式

【凸优化问题的标准形式】

标准形式的凸优化问题


\begin{align}
\min _{x \in D} \quad & f(x) \\
\text { s.t. } \quad & g_i(x) \leq 0, \quad i=1, \ldots, m \\
& A x=b
\end{align}

目标函数f、不等式约束条件g_i都是凸函数，必须是Ax=b
定义域D=\text{dom }f\cap (\cap_{i=1}^m\text{dom }g_i)通常省略
可行域为X=D\cap\{x\mid g_i(x)\leq 0,i=1,2,\cdots,m,Ax=b\}

注意：凸优化问题的可行域为凸集

定义域：目标函数f和约束函数g_i中所有变量的取值范围。
可行域：满足所有约束条件的点的集合。

【线性规划的标准形式】

标准形式的线性规划问题


\begin{align}{}
\operatorname*{min}_{x \in \mathbb{R}^n} \quad & c^\mathsf{T}x \\
\text { s.t. } \quad &Ax=b,\\
& x\geq 0.
\end{align}

【二次规划的标准形式】

二次规划的标准形式


\begin{align}{}
\operatorname*{min}_{x} \quad & \frac{1}{2}x^\mathsf{T}Px+q^\mathsf{T}x \\
\text { s.t. } \quad & x\geq 0,\\\quad &Ax=b.
\end{align}

P\in \mathcal{S}^n_+（半正定）

【半定规划的标准形式】

半定规划的标准形式


\begin{align}{}
\operatorname*{min}_{x} \quad & \langle C, X\rangle, \\
\text { s.t. } \quad & \langle A_1,X\rangle=b_1,\\
&\cdots\\
\quad &\langle A_m,X\rangle=b_m,\\
&X\succeq0.
\end{align}

Armijo准则、次梯度的定义

【Armijo准则】

设d^k是点x^k处的下降方向，若
f(x^{k}+\alpha d^{k})\le f(x^{k})+c_{1}\alpha\nabla f(x^{k})^{\mathrm{T}}d^{k},
则称步长\alpha满足\mathbf{Armijo}准则，其中c_1\in (0,1)是一个常数.

\phi(\alpha)=f(x^{k}+\alpha d^{k})可知\phi(0)=f(x^k),\phi^{\prime}(\alpha)=\nabla f(x^{k}+\alpha d^{k})^{T}d^{k}，在\alpha=0处的一阶近似为\phi(\alpha){\approx}f(x^{k})+\alpha\nabla f(x^{k})^{T}d^{k}

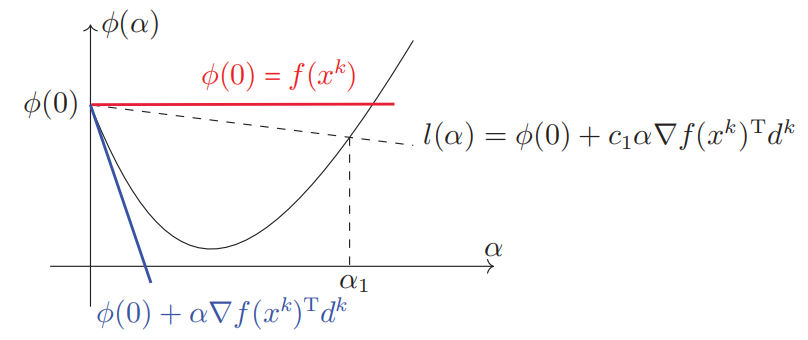
引入Armijo准则的目的是保证每一步迭代充分下降
Armijo准则有直观的几何含义，它指的是点(\alpha,\phi(\alpha))必须要在直线


l(\alpha)=\phi(0)+c_{1}\alpha\nabla f(x^{k})^{\mathrm{T}}d^{k}

的下方，上图中区间[0,\alpha_1]中的点均满足Armijo准则

参数c_1通常选一个很小的正数，例如c_1=10^{-3}

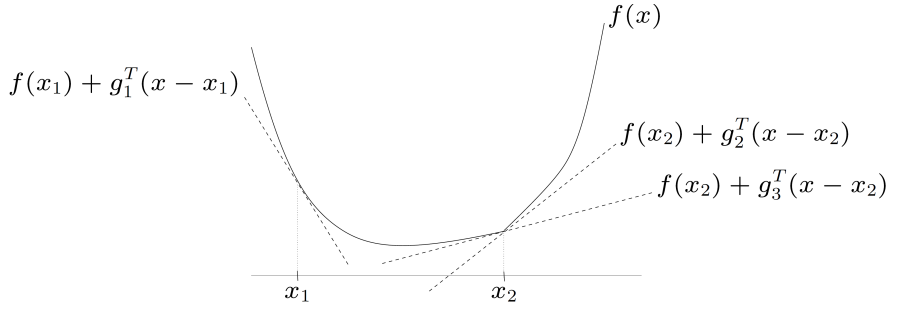
【次梯度的定义】

可微凸函数f的一阶条件：
f(y)\geq f(x)+\nabla f(x)^\mathsf{T}(y-x),
即凸函数f的线性近似总是在其下方.

设f为凸函数，x\in \mathrm{dom} f. 若向量g\in\mathbb{R}^n满足
f(y)\geq f(x)+g^\mathsf{T}(y-x),\quad \forall y\in \mathrm{dom} f,
则称g为函数f在点x处的一个次梯度.

f(x)+g^{\mathrm{T}}(y-x)是f(y)的一个全局下界
凸函数f(x)的次梯度总是存在（x是定义域的内点）
如果f是可微凸函数，那么\nabla f(x)是f在点x处的唯一次梯度
例：g_2,g_3是点x_2的次梯度，g_1是点x_1处的次梯度

拉格朗日函数、拉格朗日对偶函数、拉格朗日对偶问题、弱对偶原理、Slater条件与强对偶、KKT条件

【拉格朗日函数】

一般的约束优化问题（没有要求是凸问题）


\begin{align*}
\min_{x\in\mathbb{R}}\quad &f_0(x)\\
\text{s.t.}\quad &f_i(x)\leq 0,i = 1,\cdots,m,\\
& h_j(x)=0,j=1,\cdots ,q.
\end{align*}

最优值是p^*，可行域是所有约束条件的交集\mathcal{X}

拉格朗日函数定义L:\mathbb{R}^{n}\times\mathbb{R}_{+}^{m}\times\mathbb{R}^{q}~\to~\mathbb{R}
L(x,\lambda,\nu)=f_{0}(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{j=1}^{q}\nu_{j}h_{j}(x)
\lambda_i为第i个不等式约束的乘子

\nu_j为第j个等式约束的乘子

【拉格朗日对偶函数】

拉格朗日对偶函数g:\mathbb{R}_{+}^{m}\times\mathbb{R}^{q}~\to~[-\infty,+\infty)
\begin{align*}
g(\lambda,v)&=\inf_{x\in\mathbb{R}^n} L(x,\lambda,v)\\
&=\inf_{x\in\mathbb{R}^n} (f_{0}(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{j=1}^{q}\nu_{j}h_{j}(x))
\end{align*}

PS：inf是下界的意思

对偶函数g(\lambda, \nu)是L(x,\lambda,\nu)对任意x的下界

【弱对偶原理】

若\lambda \geq 0则g(\lambda, \nu)\leq p^*.

弱对偶原理描述了原问题和对偶问题间关系。如果\lambda\geq 0那么g(\lambda,\nu)最优值d^*永远小于等于最优值p^*

原因是因为对偶函数对于x没有限制，而拉格朗日函数对x有约束。

那么既然可行域都不一样，研究还有什么意义吗？其实对偶函数的解是拉格朗日函数解的下界，可以通过研究对偶值d^*来判断原始问题解的质量。在KKT条件下（强对偶条件），d^*=p^*。

【拉格朗日对偶问题】

拉格朗日对偶问题：


\operatorname*{max}_{\lambda\ge0,\nu}~g(\lambda,\nu)=\operatorname*{max}_{\lambda\ge0,\nu}\operatorname*{inf}_{x\in\mathbb{R}^{n}}~L(x,\lambda,\nu)

称\lambda和\nu为对偶变量，对于最优值设为d^*
d^*为p^*的最优下界，称p^*-d^*为对偶间隙
无论原问题是否为凸，拉格朗日对偶问题总是凸优化问题
\mathsf{d o m}~g=\{(\lambda,\nu)\mid\lambda\ge0,g(\lambda,\nu)>-\infty\}，其中元素称为对偶可行性解

【Slater条件与强对偶】

Slater约束品性定义：

对凸优化问题
\operatorname*{min}_{x\in\mathcal{D}}~~f_{0}(x),\quad\mathrm{s.t.}~~f_{i}(x)\color{blue}{\leqslant}\color{black}0,~i=1,2,\cdots,m,\quad A x=b,
若存在x\in\mathrm{relint}~\mathcal{D}满足
f_{i}(x)\color{red}{<}\color{black}0,\quad i=1,2,\cdots,m,\quad A x=b,
则称对此问题Slater约束品性满足. 该约束品性也称为Slater条件

\mathcal{D}是定义域，\mathrm{relint}表示相对内部，需要存在一个严格满足所有不等式约束的点，并且满足等式约束。
核心要求：Slater条件要求在凸优化问题中，至少存在一个“严格可行点”（strictly feasible point），它位于不等式约束的内部。
如果不等式约束是仿射函数时候，可以放宽，前k个不等式若仿射则可以等于

-----------------------------------
- 需要满足内部非空，而不是一个边界。例如x+y\leq 1、x\geq 0和y\geq 0组成的边界
-----------------------------------

举例（满足Slater条件）：


\begin{aligned}{}{\underset{x}{\operatorname*{min}}}\quad &{{}x_{1}^{2}+x_{2}^{2},}\\ {\mathrm{s.t.}}\quad &{{}x_{1}+x_{2}\le1,}\\ &{x_{1}-x_{2}\le1.}\end{aligned}

不等式约束形成了一个多边形区域，我们可以找到一个点x=(0,0)满足不等式约束，所以Slater条件成立，满足强对偶性。（内部非空）

几何意义：如果所有可行点都“刚好”位于约束边界例如f_i(x)=0，那么拉格朗日函数下界可能过于松弛。

通过这种几何自由度，可以证明拉格朗日乘子\lambda, \nu存在，并且优化问题的原始最优值 p^*与对偶最优值 d^*是相等的。

【强对偶性】

定理：

若凸优化问题满足Slater条件，则强对偶性成立.

Slater条件：

凸问题.
可行域内存在x使得非仿射不等式约束严格成立.

【KKT条件】

定理（凸优化问题的一阶充要条件）

考虑凸优化问题，且f_0和f_i可微，\nabla f_0,\nabla f_i表示梯度. 若强对偶性成立，则x^*和\lambda^*,\nu^*分别是原始和对偶问题的全局最优解当且仅当KKT条件成立，KKT条件为

稳定性条件 \quad 0=\nabla f_{0}\left(x^{*}\right)+\sum_{i=1}^{m} \lambda_{i}^{*} \nabla f_{i}\left(x^{*}\right)+A^{T} \nu^{*} ，

原始可行性条件 f_{i}\left(x^{*}\right) \leq 0, i=1, \cdots, m ; \quad A x^{*}=b ，

对偶可行性条件 \quad \lambda_{i}^{*} \geq 0, i=1, \cdots, m,

互补松驰条件 \quad \lambda_{i}^{*} f_{i}\left(x^{*}\right)=0, i=1, \cdots, m .

交替方向乘子法适用的类型、算法步骤

【交替方向乘子法适用的类型、算法步骤】

考虑如下凸问题：


\begin{align}
\min_{x_1,x_2}\quad &f_1(x_1)+f_2(x_2),\\
\text{s.t.}\quad &A_1x_1+A_2x_2=b
\end{align}\tag{1}\label{eq:1}

f_1,f_2是凸函数，但不要求是光滑的，x_1\in\mathbb{R}^n,x_2\in\mathbb{R}^m,A_1\in\mathbb{R}^{p\times n},A_2\in\mathbb{R}^{p\times n},b\in\mathbb{R}^p
问题特点：目标函数可以分成彼此分离的两块，但是变量被线性约束结合在一起. 常见的一些无约束和带约束的优化问题可以表示成这一形式（举例一个）
可以分成两块无约束优化问题


  \min_x\quad f_1(x)+f_2(x).

引入一个新的变量z并令x=z，将问题转化为


  \begin{aligned}
  \min_{x,z}\quad &f_1(x)+f_2(\color{blue}{z}\color{black})\\
  s.t. \quad &\color{blue}x-z=0
  \end{aligned}

【算法步骤】

首先写出问题(\ref{eq:1})的增广拉格朗日函数


  L_{\rho}(x_{1},x_{2},y){=}f_{1}(x_{1})+f_{2}(x_{2})+y^{\mathrm{T}}(A_{1}x_{1}+A_{2}x_{2}-b)+\frac{\rho}{2}\Vert A_1x_1+A_2x_2-b\Vert_2^2\tag{2}

其中y是拉格朗日乘子，\rho\gt0是二次罚项的系数.

-------------------
有些时候可能导致解不满足约束条件。
那么这个时候就加上【罚项】，达到以对不满足约束条件的解进行惩罚的效果。
可以看出，只要不满足等式那么这个罚项就会变大，这可以让优化往满足约束条件的方向进行。
-------------------

常见的求解带约束问题的增广拉格朗日函数法为如下更新：


  \begin{align}
  (x_{1}^{k+1},x_{2}^{k+1})&=\operatorname*{argmin}_{x_{1},x_{2}}L_{\rho}(x_{1},x_{2},y^{k}),\tag{3}\\
  y^{k+1}&=y^{k}+\rho(A_{1}x_{1}^{k+1}+A_{2}x_{2}^{k+1}-b).\tag{4}
  \end{align}

交替方向乘子法的基本思路：第一步迭代(3)同时对x_1和x_2进行优化有时候比较困难，而固定一个变量求解关于另一个变量的极小问题可能比较简单，因此我们可以考虑对x_1和x_2交替求极小
其迭代格式可以总结如下：


  \begin{align}
  x_{1}^{k+1}&=\underset{x_{1}}{\operatorname{argmin}} L_{\rho}\left(x_{1}, x_{2}^{k}, y^{k}\right), \tag{5}\\
  x_{2}^{k+1}&=\underset{x_{2}}{\operatorname{argmin}} L_{\rho}\left(x_{1}^{k+1}, x_{2}, y^{k}\right), \tag{6}\\
  y^{k+1}&=y^{k}+\rho\left(A_{1} x_{1}^{k+1}+A_{2} x_{2}^{k+1}-b\right) .\tag{7}
  \end{align}

计算题（我的作业）

最优化理论与方法作业 1

练习2.6:

计算下列矩阵变量函数的导数

(a) f(X) = a^\mathsf{T}Xb，这里 X \in \mathbb{R}^{m \times n}, a \in \mathbb{R}^m, b \in \mathbb{R}^n 为给定的向量。
解答:
通过定义求解，对于任意方向V\in\mathbb{R}^{m\times n}，可以求解：


   \begin{align*}
       \lim_{t\rightarrow 0}\dfrac{f(X+tV)-f(X)}{t}&=\lim_{t\rightarrow 0}\dfrac{a^\mathsf{T}(x+tV)b-a^\mathsf{T}xb}{t}\\
       &=\lim_{t\rightarrow 0}\dfrac{ta^\mathsf{T}Vb}{t}\\
       &=a^\mathsf{T}Vb\\
       &=\mathrm{Tr}(a^\mathsf{T}Vb)\\
       &=\mathrm{Tr}(ba^\mathsf{T}V)\\
       &=\langle (ba^\mathsf{T})^\mathsf{T},V\rangle\\
       &=\langle ab^\mathsf{T},V\rangle
   \end{align*}

所以f(X) = a^\mathsf{T}Xb的导数是\nabla f(X)=ab^\mathsf{T}

(b) f(X) = \mathrm{Tr}(X^\mathsf{T}AX)，其中 X \in \mathbb{R}^{m \times n} 是长方形矩阵，A 是方阵（但不一定对称）。
解答:
通过定义求解，对于任意方向V\in\mathbb{R}^{m\times n}，可以求解：


   \begin{align*}
       \lim_{t\rightarrow 0}=\dfrac{f(X+tV)-f(X)}{t}&=\lim_{t\rightarrow 0}\dfrac{\mathrm{Tr}((X+tV)^\mathsf{T}A(X+tV))-\mathrm{Tr}(X^\mathsf{T}AX)}{t}\\
       &=\lim_{t\rightarrow 0}\dfrac{\mathrm{Tr}(X^\mathsf{T}AX)+t\mathrm{Tr}(X^\mathsf{T}AV)+t\mathrm{Tr}(V^\mathsf{T}AX)+t^2\mathrm{Tr}(V^\mathsf{T}AV)-\mathrm{Tr}(X^\mathsf{T}AX)}{t}\\
       &=\lim_{t\rightarrow 0}\dfrac{t(\mathrm{Tr}(X^\mathsf{T}AV)+\mathrm{Tr}(V^\mathsf{T}AX))+t^2\mathrm{Tr}(V^\mathsf{T}AV)}{t}\\
       &=\mathrm{Tr}(X^\mathsf{T}AV)+\mathrm{Tr}(V^\mathsf{T}AX)\\
       &=\langle A^\mathsf{T}X,V\rangle+\langle V,AX\rangle\\
       &=\langle A^\mathsf{T}X+AX,V\rangle
   \end{align*}

所以f(X) = \mathrm{Tr}(X^\mathsf{T}AX)的导数是\nabla f(X)=A^\mathsf{T}X+AX

练习2.7

1.考虑二次不等式
x^\mathsf{T}Ax+b^\mathsf{T}x+c\leq 0
其中A为n阶对称矩阵，设C为上述不等式的解集.

(a) 证明：当 A 正定时，C 为凸集。

解答:
对于二次不等式x^\mathsf{T}Ax+b^\mathsf{T}x+c\leq 0进行分析，因为矩阵A对称正定，所以x^\mathsf{T}Ax> 0恒成立，所以该二次型是关于x的凸函数。并且b^\mathsf{T}x+c是线性函数，即x^\mathsf{T}Ax+b^\mathsf{T}x+c\leq 0也是个凸函数，该问题是一个凸优化问题。
要证明C为凸集，则可以利用凸函数的下水平集是凸集的性质，因此集合C是凸函数f(x)对应的下水平集：


C=\{x\in\mathbb{R}^{n}|f(x)\leq 0\}

因此C是凸集，证毕。
也可以通过定义证明，要想证明C是凸集，对于集合C，对于任意的x_1,x_2\in C且\theta\in [0,1]，都有


x=\theta x_1+(1-\theta)x_2\in C

则C为凸集。
现在对于任意的x_1,x_2\in C且\theta\in [0,1]，有


\begin{align*}
    f(x_1)&=x_1^\mathsf{T}Ax_1+b^\mathsf{T}x_1+c\leq 0\\
    f(x_2)&=x_2^\mathsf{T}Ax_2+b^\mathsf{T}x_2+c\leq 0\\
    x&=\theta x_1+(1-\theta)x_2
\end{align*}

代入f(x)中有：


\begin{align*}
f(x)&=f(\theta x_1+(1-\theta)x_2)\\
&=(\theta x_1+(1-\theta)x_2)^\mathsf{T}A(\theta x_1+(1-\theta)x_2)+b^\mathsf{T}(\theta x_1+(1-\theta)x_2)+c\\
&=\theta^2x_1^\mathsf{T}Ax_1+(1-\theta)^2x_2^\mathsf{T}Ax_2+\theta x_1^\mathsf{T}(1-\theta)x_2+(1-\theta)x_2^\mathsf{T}A\theta x_1+\theta b^\mathsf{T}x_1+(1-\theta)b^\mathsf{T}x_2+c
\end{align*}

利用凸函数的性质，若证明C为凸集，即证明x\in C，则需要满足


f(\theta x_1+(1-\theta)x_2)\leq \theta f(x_1)+(1-\theta)f(x_2)\leq 0

我们先计算该线性组合：


\begin{align*}
    \theta f(x_1) + (1-\theta)f(x_2) &= \theta \left( x_1^\mathsf{T}Ax_1 + b^\mathsf{T}x_1 + c \right) + (1-\theta) \left( x_2^\mathsf{T}Ax_2 + b^\mathsf{T}x_2 + c \right) \\
&= \theta x_1^\mathsf{T}Ax_1 + \theta b^\mathsf{T}x_1 + \theta c + (1-\theta)x_2^\mathsf{T}Ax_2 + (1-\theta)b^\mathsf{T}x_2 + (1-\theta)c \\
&= \theta x_1^\mathsf{T}Ax_1 + (1-\theta)x_2^\mathsf{T}Ax_2 + \theta b^\mathsf{T}x_1 + (1-\theta)b^\mathsf{T}x_2 + c
\end{align*}

我们将二者做差，可以得到：


\begin{align*}
    \theta f(x_1) + (1-\theta)f(x_2) - f(\theta x_1 + (1-\theta)x_2) &= \theta \left( x_1^\mathsf{T}Ax_1 + b^\mathsf{T}x_1 + c \right) + (1-\theta)\left( x_2^\mathsf{T}Ax_2 + b^\mathsf{T}x_2 + c \right) \\
    &\quad - \left( \theta^2 x_1^\mathsf{T}Ax_1 + 2\theta(1-\theta)x_1^\mathsf{T}Ax_2 + (1-\theta)^2 x_2^\mathsf{T}Ax_2 \right. \\
    &\quad \left. + \theta b^\mathsf{T}x_1 + (1-\theta)b^\mathsf{T}x_2 + c \right) \\
    &= \theta x_1^\mathsf{T}Ax_1 + (1-\theta)x_2^\mathsf{T}Ax_2 + \theta b^\mathsf{T}x_1 + (1-\theta)b^\mathsf{T}x_2 + c \\
    &\quad - \theta^2 x_1^\mathsf{T}Ax_1 - 2\theta(1-\theta)x_1^\mathsf{T}Ax_2 - (1-\theta)^2 x_2^\mathsf{T}Ax_2 \\
    &= \theta(1-\theta)x_1^\mathsf{T}Ax_1 + (1-\theta)\theta x_2^\mathsf{T}Ax_2 - 2\theta(1-\theta)x_1^\mathsf{T}Ax_2 \\
    &= \theta(1-\theta) \left( x_1^\mathsf{T}Ax_1 + x_2^\mathsf{T}Ax_2 - 2x_1^\mathsf{T}Ax_2 \right) \\
    &= \theta(1-\theta) (x_1 - x_2)^\mathsf{T}A(x_1 - x_2)
\end{align*}

因为A是对称正定的，所以\forall x都满足x^\mathsf{T}Ax >0，那么(x_1-x_2)^\mathsf{T}A(x_1-x_2)>0，因为\theta\in [0,1]，所以\theta (1-\theta)\geq 0，所以等式左边恒大于，即


\begin{align*}
    &\theta f(x_1) + (1-\theta)f(x_2) - f(\theta x_1 + (1-\theta)x_2) \geq 0\\
    &f(\theta x_1 + (1-\theta)x_2) \leq \theta f(x_1) + (1-\theta)f(x_2)\leq 0
\end{align*}

所以x=\theta x_1+(1-\theta)x_2\in C，C是一个凸集，证毕。

(b) 设 C^\prime 是 C 和超平面 g^\mathsf{T} x + h = 0 的交集（g \neq 0），若存在 \lambda \in \mathbb{R}，使得 A + \lambda g g^\mathsf{T} 半正定，证明：C^\prime 为凸集。

解答:
首先通过第一问我们可以得到当A是正定的时候，x^\mathsf{T}Ax+b^\mathsf{T}x+c\leq 0的解集是一个凸集，如果是半正定同理也可以。
现在有g^\mathsf{T}+h=0的约束条件，C^\prime是C和g^\mathsf{T}x+h=0的交集，若要证明C^\prime是凸集，则需要在f(x)基础上加上约束条件并证明其是凸函数。
考虑到f(x)中有二次型x^\mathsf{T}Ax，我们可以增加(g^\mathsf{T}x+h)^2=0的约束条件，并且引入\lambda，可以构造：


\begin{align*}
g(x)&=x^\mathsf{T}Ax+b^\mathsf{T}x+c+\lambda(g^\mathsf{T}x+h)^2\\
&=x^\mathsf{T}Ax+b^\mathsf{T}x+c+\lambda(g^\mathsf{T}x)^2+2\lambda hg^\mathsf{T}x+\lambda h^2\\
&=x^T(A+\lambda gg^\mathsf{T})x+(b^\mathsf{T}+2\lambda hg^\mathsf{T})x+\lambda h^2+c
\end{align*}

现在对g(x)进行分析，其中二次型为x^T(A+\lambda gg^\mathsf{T})x，因为A+\lambda gg^\mathsf{T}是半正定的，所以该二次型是凸函数。而线性部分为(b^\mathsf{T}+2\lambda hg^\mathsf{T})x+\lambda h^2+c也是线性函数，所以g(x)是凸函数。
因为g(x)是一个凸函数，所以其的解集是凸集。因为该函数是由f(x)和约束条件构成的，所以C^\prime就是该解集，即C^\prime就是凸集，证毕。

答案做法（我觉得我的方法比答案好）

练习2.12

1.求下列函数的共轭函数

(b) 矩阵对数：f(x) = -\ln \det(X)

解答:
对于函数 f(X) = -\ln \det(X)，其共轭函数是f^*(X)\sup_{x\in\text{dom }f}(\mathrm{Tr}(Y^\mathsf{T}X)-f(X))，我们令函数\


g(X)=\mathrm{Tr}(Y^\mathsf{T}X)-f(X)=\mathrm{Tr}(Y^\mathsf{T}X)+\ln\det(X)

对其求导，使用行列式求导公式\dfrac{\partial\det (X)}{\partial X}=\det(X)(X^{-1})^\mathsf{T}，并另其等于可以得到


\begin{align*}
    g^\prime(X)&=Y+\dfrac{1}{\det(X)}\cdot\dfrac{\partial\det(X)}{\partial (X)}\\
    &= Y+\dfrac{1}{\det(X)}\cdot\det(X)(X^{-1})^\mathsf{T}\\
    &=Y+(X^{-1})^\mathsf{T} =0
\end{align*}

这样就可以得到


X^*=-(Y^{-1})^\mathsf{T}

那么对于共轭函数f^*(Y)=g(X)=\mathrm{Tr}(Y^\mathsf{T}X)+\ln\det(X)则有


\begin{align*}
f^*(Y)&=\mathrm{Tr}(Y^\mathsf{T}(-(Y^{-1})^\mathsf{T}))+\ln\det(-(Y^{-1})^\mathsf{T})\\
&=\mathrm{Tr}(-Y^\mathsf{T}\cdot(Y^\mathsf{T})^{-1})+\ln\det(-Y^{-1})\\
&=\mathrm{Tr}(-I)-\ln\det(-Y)\\
&=-n-\ln\det(-Y)
\end{align*}

所以，f(X) = -\ln \det(X)共轭函数为-n-\ln\det(-Y)，并且需要满足Y\prec 0.

最优化理论与方法作业 2

一、计算次梯度

1.求下列函数的一个次梯度

(a) f(x)=\Vert Ax-b\Vert_2+\Vert x\Vert_2;

(b) f(x)=\inf_y\Vert Ay-x\Vert_\infty 这里可以假设能够取到\hat{y}，使得\Vert A\hat{y}-x\Vert_\infty=f(x).

解答 (a):
令f_1(x)=\Vert Ax-b\Vert_2, f_2(x)=\Vert x\Vert_2, 则f(x)=f_1(x)+f_2(x)，分别处理
对于f_1(x)=\Vert Ax-b\Vert_2，令u=(Ax_1-b)^2+(Ax_2-b)^2+\cdots+(Ax_n-b)^2，则f_1(x)=\sqrt{u}，f_1(x)在Ax-b\neq 0时可微，梯度为


\begin{align*}
    \dfrac{\partial{f_1(x)}}{\partial{x_i}}&=\dfrac{\partial{f_1(x)}}{\partial{u}}\cdot \dfrac{\partial{u}}{\partial{x_i}}\\
    &=\dfrac{1}{2\sqrt{u}}\cdot 2A^\mathsf{T}(Ax_i-b)\\
    &=A^\mathsf{T}\dfrac{Ax_i-b}{\Vert Ax_i-b\Vert_2}\\
    \dfrac{\partial f_1(x)}{\partial x}&=A^\mathsf{T}\dfrac{Ax-b}{\Vert Ax-b\Vert_2}
\end{align*}

f_1(x) 在 Ax-b=0 不可微，此时的次梯度为 \{A^\mathsf{T} u\mid\Vert u\Vert_2\leq 1\}
这里小于等于1是因为泰勒展开之后\Vert y\Vert_2\geq \nabla f_1(x)^T\cdot y，由于柯西施瓦茨不等式得u^\mathsf{T} y\leq \Vert u\Vert_2\cdot\Vert y\Vert_2，所以需要满足\Vert u\Vert_2\leq 1.
同理对于f_2(x)=\Vert x\Vert_2有当x\neq 0时候，f_2(x)可微，梯度为


\begin{align*}
    \dfrac{\partial{f_2(x)}}{\partial{x_i}}&=\dfrac{\partial{f_2(x)}}{\partial{u}}\cdot \dfrac{\partial{u}}{\partial{x_i}}\\
    &=\dfrac{1}{2\sqrt{u}}\cdot 2x_i\\
    &=\dfrac{x_i}{\Vert x\Vert_2}\\
    \dfrac{\partial f_2(x)}{\partial x}&=\dfrac{x}{\Vert x\Vert_2}
\end{align*}

f_2(x) 在 x=0 不可微，此时的次梯度为 \partial f_2(0)=\{u\mid\Vert u\Vert_2\leq 1\} (与上方同理)
故f(x)在x处的一个次梯度为


g=\begin{cases}
        A^\mathsf{T}\dfrac{Ax-b}{\Vert Ax-b\Vert_2}+\dfrac{x}{\Vert x\Vert_2}&Ax-b\neq 0,x\neq 0\\
        \{A^\mathsf{T} u\mid\Vert u\Vert_2\leq 1\}+\{v\mid\Vert v\Vert_2\leq 1\}&\text{其他}
    \end{cases}

解答 (b):
令u=A\hat{y}-x，则f(x)=\Vert u\Vert_\infty,无穷范数取每一个分量绝对值最大的，可以记


I=\{ i\mid \lvert x \rvert = \Vert u\Vert_\infty\}

这样I表示能够取到最大值的分量的下标集合，对于其他的分量需要满足绝对值小于等于1.
对于每一个i\in I，有


\begin{align*}
g_i&=\dfrac{\partial \lvert u_i \rvert}{\partial x_i}\\
&=\dfrac{\partial \lvert (A\hat{y})_i-x_i\rvert}{\partial x_i}\\
&=-\mathrm{sign}(u_i)=-\mathrm{sign}((A\hat{y})_i-x_i)
\end{align*}

其中\mathrm{sign}(u_i)表示u_i的符号，对于其他的分量(i\notin I)，需要满足\lvert g_i \rvert\leq 1
故f(x)在x处的一个次梯度为


g=\begin{cases}
        -\mathrm{sign}((A\hat{y})_i-x_i)&i\in I\\
        \{g_i\mid |g_i|\leq 1\}&i\notin I
    \end{cases}

-------------------------------------------------
答案和我的有些不太一样，但是也差不多。我不太能理解为什么答案有的时候不写次梯度的范围

-------------------------------------------------

二、线性规划

1.将下面问题转化为线性规划：给定A\in\R^{m\times n},b\in\R^m

(a) \min_{x \in \mathbb{R}^{n}}\|A x-b\|_{1}, \quad \text{s.t. } \|x\|_{\infty} \leqslant 1

(b) \min_{x \in \mathbb{R}^{n}}\|x\|_{1} , \text{s.t. } \|A x-b\|_{\infty} \leqslant 1

(c) \min_{x \in \mathbb{R}^{n}}\|A x-b\|_{1}+\|x\|_{\infty}

(d) \min_{x \in \mathbb{R}^{n}}\sum_{i=1}^{m} \max \left\{0, a_{i}^{\mathrm{T}} x+b_{i}\right\}.

解答 (a):
引入z_i，使得|Ax_i-b_i|\leq z_i，则问题(a)可以转化为


\begin{aligned}
    \min_{x,z}\quad &\sum_{i=1}^{m}z_i\\
    \text{s.t.}\quad  &-z_i\leq Ax_i-b_i\leq z_i\\
    &\|x\|_\infty\leq 1\\
    &z_i\geq 0
\end{aligned}

解答 (b):
引入z_i，使得|x_i|\leq z_i，则问题(b)可以转化为


\begin{aligned}
    \min_{x\in\R^n,z}\quad &\sum_{i=1}^{n}z_i\\
    \text{s.t.}\quad  &-z_i\leq x_i\leq z_i\\
    &\|Ax-b\|_\infty\leq 1\\
    &z_i\geq 0
\end{aligned}

在这里\Vert Ax-b\Vert_\infty\leq 1等价于-1\leq (Ax)_i-b_i\leq 1.

解答 (c):
对于\Vert Ax-b\Vert_1引入z_i，则有


\begin{aligned}
    \Vert Ax-b\Vert_1&=\sum_{i=1}^{m}z_i\\
    \text{s.t.}\quad &-z_i\leq (Ax)_i-b_i\leq z_i\\
    z_i\geq 0
\end{aligned}

对于\Vert x\Vert_\infty引入t，则有


\begin{aligned}
    \Vert x\Vert_\infty&\leq t\\
    \text{s.t.}\quad &-t\leq x_i\leq t\\
    t\geq 0
\end{aligned}

所以可以转化为如下问题：


\begin{aligned}
    \min_{x\in\R^n,z,t}\quad &\sum_{i=1}^{m}z_i+t\\
    \text{s.t.}\quad &-z_i\leq (Ax)_i-b_i\leq z_i\\
    &-t\mathbf{1}\leq x\leq t\mathbf{1}\\
    &z_i\geq 0,t\geq 0
\end{aligned}

解答 (d):
引入z_i，令z_i\geq \max \{0,a_i^\mathsf{T} x+b_i\}，即


z_i\geq a_i^\mathsf{T} x+b_i,z_i\geq 0

则问题(d)可以转化为


\begin{aligned}
    \min_{x\in\R^n,z}\quad &\sum_{i=1}^{m}z_i\\
    \text{s.t.}\quad &z_i\geq a_i^\mathsf{T} x+b_i\\
    &z_i\geq 0
\end{aligned}

这里也可以写作z\geq Ax+b.

三、复合函数计算导数

1.在数据插值中，考虑一个简单的复合模型（取\phi为恒等映射，两层复合模型）：
\min_{X_1\in\R^{q\times p},X_2\in\R^{q\times q}} \sum_{i=1}^m\Vert X_2X_1a_i-b_i\Vert_2^2,
其中a_i\in\R^p,b_i\in\R^q,i=1,2,\cdots,m.

(a)试计算目标函数关于X_1,X_2的导数；

(b)试给出该问题的最优解.

解答 (a):
这里方便计算，引入如下变量A,B：


A=(a_1,a_2,\cdots,a_m)^\mathsf{T},B=(b_1,b_2,\cdots,b_m)^\mathsf{T}\\
A\in\R^{m\times p},B\in\R^{m\times q}

那么问题可以写作


f(X_1,X_2)=\sum_{i=1}^m\Vert X_2X_1a_i-b_i\Vert_2^2=\Vert X_2X_1A-B\Vert_F^2

这里\Vert \cdot \Vert_F表示Frobenius范数。
对f(X_1,X_2)可以展开为：


\begin{aligned}
    f(X_1,X_2)&=\Vert X_2X_1A-B\Vert_F^2\\
    &=\mathrm{Tr}((X_2X_1A-B)(X_2X_1A-B)^\mathsf{T})\\
    &=\mathrm{Tr}(X_2X_1AA^\mathsf{T} X_1^\mathsf{T} X_2^\mathsf{T})-2\mathrm{Tr}(BA^\mathsf{T} X_1^\mathsf{T} X_2^\mathsf{T})+\mathrm{Tr}(BB^\mathsf{T})
\end{aligned}

对于X_1求导，有


\begin{aligned}
\dfrac{\partial f}{\partial X_1}&= \dfrac{\partial}{\partial X_1}\mathrm{Tr}(X_2X_1AA^\mathsf{T} X_1^\mathsf{T} X_2^\mathsf{T})-2\dfrac{\partial}{\partial X_1}\mathrm{Tr}(BA^\mathsf{T} X_1^\mathsf{T} X_2^\mathsf{T})+\dfrac{\partial}{\partial X_1}\mathrm{Tr}(BB^\mathsf{T})\\
&=(AA^\mathsf{T} X_1^\mathsf{T} X_2^\mathsf{T} X_2)^\mathsf{T}+X_2^TX_2X_1AA^\mathsf{T}-2X_2^\mathsf{T} BA^\mathsf{T}+0\\
&=2X_2^\mathsf{T} X_2X_1AA^\mathsf{T}-2X_2^\mathsf{T} BA^\mathsf{T} \\
&=2X_2^\mathsf{T} (X_2X_1A-B)A^\mathsf{T}
\end{aligned}

对于X_2求导，同理有


\dfrac{\partial f}{\partial X_2}=2(X_2X_1A-B)A^\mathsf{T} X_1^\mathsf{T}

所以目标函数关于X_1,X_2的导数分别为：


\dfrac{\partial f}{\partial X_1}=2X_2^\mathsf{T} (X_2X_1A-B)A^\mathsf{T},\quad \dfrac{\partial f}{\partial X_2}=2(X_2X_1A-B)A^\mathsf{T} X_1^\mathsf{T}

解答 (b):
有(a)中可以将问题转化求解\min \Vert X_2X_1A-B\Vert_F^2，这里令X=X_2X_1，则问题可以转化为


\min_{X\in\R^{q\times p}}\Vert XA-B\Vert_F^2

令g(X)=\Vert XA-B\Vert_F^2，则有


\begin{aligned}
    g(X)&=\Vert XA-B\Vert_F^2\\
    &=\mathrm{Tr}((XA-B)(XA-B)^\mathsf{T})\\
    &=\mathrm{Tr}(XAA^\mathsf{T} X^\mathsf{T})-2\mathrm{Tr}(BA^\mathsf{T} X^\mathsf{T})+\mathrm{Tr}(BB^\mathsf{T})
\end{aligned}

对函数g(X)求导，有


\begin{aligned}
\dfrac{\partial g}{\partial X}&=2XAA^\mathsf{T}-2BA^\mathsf{T}\\
&=2(XA-B)A^\mathsf{T}
\end{aligned}

令导数为，有XA=B，即X=BA^{-1}，所以问题的最优解需要X_1,X_2满足X_2X_1=BA^{-1}即可取到函数的最小值.

最优化理论与方法作业 3

一、梯度法的精确步长

1.f为正定二次函数f(x)=\frac{1}{2}x^\mathsf{T} Ax+b^\mathsf{T} x，d^k为下降方向，x^k为当前迭代点. 试求出精确线搜索步长
\begin{equation}
    \alpha_k=\arg\min_{\alpha>0}f(x^k+\alpha d^k)\notag
\end{equation}
并由此推出最速下降法的步长满足(6.2.2)式（见定理6.2）.

解答:
首先我们对目标函数f(x^k+\alpha d^k)进行展开得到：


\begin{align*}
    f(x^k+\alpha d^k)&=\frac{1}{2}(x^k+\alpha d^k)^\mathsf{T} A(x^k+\alpha d^k)+b^\mathsf{T} (x^k+\alpha d^k)\\
    &= \frac{1}{2}((x^k)^\mathsf{T} +\alpha (d^k)^\mathsf{T})A(x^k+\alpha d^k)+b^\mathsf{T} x^k+\alpha b^\mathsf{T} d^k\\
    &=\frac{1}{2}[(x^k)^\mathsf{T} Ax^k+\alpha (x^k)^\mathsf{T} Ad^k+\alpha(d^k)^\mathsf{T} Ax^k+\alpha^2 (d^k)^\mathsf{T} d^k]+b^Tx^k+\alpha b^\mathsf{T} d^k\tag{1}
\end{align*}

因为f为正定二次函数，所以A需要满足对称正定，所以有(x^k)^\mathsf{T} Ad^k=(d^k)^\mathsf{T} Ax^k，所以上式(1)可以化简为：


\begin{align*}
    f(x^k+\alpha d^k)&=\frac{1}{2}[(x^k)^\mathsf{T} Ax^k+2\alpha (x^k)^\mathsf{T} Ad^k+\alpha^2 (d^k)^\mathsf{T} d^k]+b^Tx^k+\alpha b^\mathsf{T} d^k\\
    &=\frac{1}{2}(x^k)^\mathsf{T} Ax^k+\alpha (x^k)^\mathsf{T} Ad^k+\frac{1}{2}\alpha^2 (d^k)^\mathsf{T} Ad^k+b^\mathsf{T} x^k+\alpha b^Td^k\\
    &=f(x^k)+\alpha (x^k)^\mathsf{T} Ad^k+\frac{1}{2}\alpha^2(d^k)^\mathsf{T} Ad^k+\alpha b^Td^k\\
    &=f(x^k)+\alpha ((x^k)^\mathsf{T} Ad^k+b^Td^k)+\frac{1}{2}\alpha^2(d^k)^\mathsf{T} Ad^k \tag{2}
\end{align*}

因为f(x)的梯度为\nabla f(x)=Ax+b，所以有\nabla f(x^k)=Ax^k+b，所以有：


\begin{align*}
    \nabla f(x^k)^\mathsf{T} d^k=(x^k)^\mathsf{T} Ad^k+b^\mathsf{T} d^k
\end{align*}

代入(2)式中得到：


\begin{align*}
    f(x^k+\alpha d^k)=f(x^k)+\alpha \nabla f(x^k)^\mathsf{T} d^k+\frac{1}{2}\alpha^2(d^k)^\mathsf{T} Ad^k
\end{align*}

要求出\alpha_k，只需要对上式求导数并令其为0即可：


\begin{align*}
    \frac{d}{d\alpha}f(x^k+\alpha d^k)=\nabla f(x^k)^\mathsf{T} d^k+\alpha(d^k)^\mathsf{T} Ad^k=0
\end{align*}

可以得到：


\begin{align*}
    \alpha_k=-\frac{\nabla f(x^k)^\mathsf{T} d^k}{(d^k)^\mathsf{T} Ad^k}
\end{align*}

而最速下降法的下降方向d^k=-\nabla f(x^k)，所以有：


\begin{align*}
    \alpha_k=-\frac{\nabla f(x^k)^\mathsf{T} (-\nabla f(x^k))}{(-\nabla f(x^k))^\mathsf{T} A(-\nabla f(x^k))}=\frac{\nabla f(x^k)^\mathsf{T} \nabla f(x^k)}{\nabla f(x^k)^\mathsf{T} A\nabla f(x^k)}
\end{align*}

所以得到了最速下降法的步长满足(6.2.2)式：


\begin{align*}
    \alpha_k=\frac{\Vert \nabla f(x^k)\Vert ^2}{\nabla f(x^k)^\mathsf{T} A\nabla f(x^k)}
\end{align*}

最优化理论与方法作业 4

一、对偶问题

1.计算下列优化问题的对偶问题.

(a) \min_{x\in\R^n} \quad \Vert x\Vert_1, s.t. Ax=b;

(b) \min_{x\in\R^n} \quad \Vert Ax-b\Vert_1;

(c) \min_{x\in\R^n} \quad \Vert Ax-b\Vert_\infty;

(d) \min_{x\in\R^n} \quad x^\mathsf{T} Ax+2b^\mathsf{T} x, s.t. \Vert x\Vert_2^2\leq 1,其中A为正定矩阵.

解答 (a):
引入拉格朗日乘子\nu\in\R^m，构造拉格朗日函数


\begin{align*}
    L(x,\nu)&=\Vert x\Vert_1+\nu^\mathsf{T}(Ax-b)\notag\\
    &=\sum_{i=1}^n(\vert x_i\vert+\color{red}\nu_i^\mathsf{T} a_i x_i\color{black})-\nu^\mathsf{T} b\notag
\end{align*}

感谢楠姐的提醒，其实这里不能写成\color{red}\nu_i^\mathsf{T} a_i x_i，因为这样首先a_i没有定义，就算是列向量的话，三个的乘法是数乘向量乘数，所以并不是一个标量，应该写成\sum \nu_ia_i^\mathsf{T}x。这样x是单独的，而前面的系数好进行分析。
在这个题的所有小问可能都有该问题
推荐：有一个好的办法是，我们可以令\color{blue}c=A^\mathsf{T}\nu，这样对c_i进行分析会好一些（像答案那样，如下图）

要使得\min_x L(x,\nu)存在，需要满足\forall i\in\{1,2,\cdots,n\}，有


\begin{align*}
-1\leq \nu_i^\mathsf{T} a_i\leq 1\notag
\end{align*}

即可以写作


\begin{align*}
&\vert \nu_i^\mathsf{T} a_i\vert\leq 1\notag,\forall i\in\{1,2,\cdots,n\}\\
&\Vert \nu^\mathsf{T} A\Vert_\infty\leq 1\notag
\end{align*}

由此可以得到对偶问题


\begin{align*}
    \max \quad &-\nu^\mathsf{T} b,\notag\\
    \text{s.t.}\quad &\Vert \nu^\mathsf{T} A\Vert_\infty\leq 1.\notag
\end{align*}

解答 (b):
令y=Ax-b，则原问题可以写作


\begin{align*}
    \min_{y\in\R^m} \quad &\Vert y\Vert_1\notag\\
    \text{s.t.}\quad &Ax-b=y\notag
\end{align*}

引入拉格朗日乘子\nu\in\R^m，构造拉格朗日函数


\begin{align*}
    L(y,\nu)&=\Vert y\Vert_1+\nu^\mathsf{T}(Ax-b-y)\notag\\
    &=\Vert y\Vert_1+\nu^\mathsf{T} Ax-\nu^\mathsf{T} y-\nu^\mathsf{T} b\notag
\end{align*}

要使得\min_y L(y,\nu)存在，需要满足\forall i\in\{1,2,\cdots,m\}，有


\begin{align*}
-1\leq \nu_i\leq 1\\
\nu^\mathsf{T} A=0
\end{align*}

即可以写作


\begin{align*}
    \Vert \nu\Vert_\infty\leq 1\\
    \nu^\mathsf{T} A=0
\end{align*}

由此可以得到对偶问题


\begin{align*}
    \max \quad &-\nu^\mathsf{T} b,\\
    \text{s.t.}\quad &\Vert \nu\Vert_\infty\leq 1,\\
    &\nu^\mathsf{T} A=0.
\end{align*}

解答 (c):


\min_{x\in\mathbb{R}^n}\quad \Vert Ax-b\Vert_\infty

令t=\Vert Ax-b\Vert_\infty，则有：


\begin{aligned}
Ax-b&\leq t\mathbf{1},\\
Ax-b&\geq -t\mathbf{1}.
\end{aligned}\notag

因为我们的\lambda_1,\lambda_2为非负，所以同一写成小于等于的形式，有:


\begin{aligned}
Ax-b-t\mathbf{1}&\leq 0,\\
-t\mathbf{1}-Ax+b&\leq 0.
\end{aligned}\notag

那么则有拉格朗日函数L(x,t,\lambda_1,\lambda_2):


L(x,t,\lambda_1,\lambda_2)=t+\lambda_1^\mathsf{T}(Ax-b-t\mathbf{1})+\lambda_2^\mathsf{T}(-t\mathbf{1}-Ax+b)

对x,t分别求导，有：


\begin{aligned}
\dfrac{\partial L}{\partial x}&=\lambda_1^\mathsf{T}A-\lambda_2^\mathsf{T}A=0\\
\dfrac{\partial L}{\partial t}&=1-\lambda_1^\mathsf{T}\mathbf{1}-\lambda_2^\mathsf{T}\mathbf{1}=0
\end{aligned}\notag

L有最小值，对偶问题为


\begin{aligned}
\max \quad &-\lambda_1^\mathsf{T}b+\lambda_2^\mathsf{T}b\\
\mathrm{s.t.}\quad &\lambda_1^\mathsf{T}A-\lambda_2^\mathsf{T}A=0\\
&1-\lambda_1^\mathsf{T}\mathbf{1}-\lambda_2^\mathsf{T}\mathbf{1}=0\\
&\lambda_1,\lambda_2\geq 0
\end{aligned}\notag

解答 (d):
\Vert x\Vert_2^2\leq 1可以写作x^\mathsf{T} x\leq 1，引入拉格朗日乘子\lambda\in\R，构造拉格朗日函数


\begin{align*}
    L(x,\lambda)&=x^\mathsf{T} Ax+2b^\mathsf{T} x+\lambda(x^\mathsf{T} x-1)\notag\\
    &=x^T(A+\lambda I)x+2b^\mathsf{T} x-\lambda\notag
\end{align*}

设对偶函数为g(\lambda)=\inf_x L(x,\lambda)，则需要满足\forall x\in\R^n，有


\begin{align*}
    \nabla_x L(x,\lambda)=2(A+\lambda I)x+2b=0\notag
\end{align*}

解得


\begin{align*}
    x=-(A+\lambda I)^{-1}b\notag
\end{align*}

代入L(x,\lambda)得到


\begin{align*}
    g(\lambda)=-b^\mathsf{T}(A+\lambda I)^{-1}b-\lambda\notag
\end{align*}

由于A是正定矩阵，所以在\lambda\geq 0情况下，A+\lambda I也为正定矩阵，所以此时逆矩阵存在，所以对偶问题为


\begin{align*}
    \max \quad &-b^\mathsf{T}(A+\lambda I)^{-1}b-\lambda\notag\\
    \text{s.t.}\quad &\lambda\geq 0\notag
\end{align*}

二、KKT点

考虑优化问题


\begin{align*}
\min_{x\in\R^2}\quad &x_1,\\
\text{s.t.}\quad &16-(x_1-4)^2-x_2^2\geq 0,\\
\quad &x_1^2+(x_2-2)^2-4=0.
\end{align*}

求出该优化问题的KKT点.

解答:
首先将16-(x_1-4)^2-x_2^2\geq 0写作x_1^2-8x_1+x_2^2\leq 0，
引入拉格朗日乘子\lambda,\nu\geq 0，构造拉格朗日函数


\begin{align*}
    L(x_1,x_2,\lambda,\nu)&=x_1+\lambda(x_1^2-8x_1+x_2^2)+\nu(x_1^2+(x_2-2)^2-4)\notag\\
    &=(\lambda+\nu)x^2+(1-8\lambda)x_1+(\lambda+\nu)x_2^2-4\nu x_2
\end{align*}

对x_1,x_2分别求导数得到


\begin{align*}
    \frac{\partial L}{\partial x_1}&=2(\lambda+\nu)x_1+(1-8\lambda)=0\notag\\
    \frac{\partial L}{\partial x_2}&=2(\lambda+\nu)x_2-4\nu=0\notag
\end{align*}

互补松弛条件为\lambda(x_1^2-8x_1+x_2^2)=0,\lambda\geq 0，并且等式约束满足x_1^2+(x_2-2)^2-4=0，同时原始的约束条件为16-(x_1-4)^2-x_2^2\geq 0，若\lambda =0则稳定性条件为


\begin{align*}
    2\nu x_1+1=0,\\
    2\nu x_2-4\nu=0.
\end{align*}

代入等式约束可以得到:x_1=\pm 2，此时得到KKT点为(2,2,0,-\frac{1}{4})和(-2,2,0,\frac{1}{4}).但第二个不满足条件，只有第一个满足，所以取(2,2,0,-\frac{1}{4})为KKT点.
若\lambda >0，此时不等式约束为


x_1^2-8x_1+x_2^2=0

结合等式约束解方程组：


\begin{align*}
\begin{cases}
    x_1^2-8x_1+x_2^2=0\\
    x_1^2+(x_2-2)^2-4=0
\end{cases}
\end{align*}

得到解为(x_1,x_2)=(0,0)和(x_1,x_2)=(\frac{8}{5},\frac{16}{5})
检查这些点是否满足不等式约束，即都满足。
所以KKT点为(0,0,\frac{1}{8},0)和(\frac{8}{5},\frac{16}{5},\frac{3}{40},-\frac{1}{5})和(2,2,0,-\frac{1}{4}).

三、支持向量机

考虑支持向量机问题
\begin{align*}
\min_{x\in\R^n,\zeta}\quad &\frac{1}{2}\Vert x\Vert_2^2+\mu\sum_{i=1}^m\zeta_i,\\
\text{s.t.}\quad &b_ia_i^\mathsf{T} \geq 1-\zeta_i, i=1,2,\cdots,m,\\
&\zeta_i\geq 0, i=1,2,\cdots,m.
\end{align*}
其中\mu> 0为常数且b_i\in\R,a_i\in\R^n,i=1,2,\cdots,m是已知的。写出该问题的对偶问题。

解答:
首先对于不等式约束写作


\begin{align*}
1-\zeta_i -b_ia_i^\mathsf{T} \leq 0\\
-\zeta_i\leq 0\notag
\end{align*}

首先构建拉格朗日函数，引入拉格朗日乘子\lambda\in\R^m,\nu\in\R^m，构造拉格朗日函数


\begin{align*}
L(x,\zeta,\lambda,\nu)&=\frac{1}{2}\Vert x\Vert_2^2+\mu\sum_{i=1}^m\zeta_i+\sum_{i=1}^m\lambda_i(1-\zeta_i-b_ia_i^\mathsf{T})-\sum_{i=1}^m\nu_i\zeta_i\notag\\
&=\frac{1}{2}\|x\|_{2}^{2}-(\sum_{i=1}^{m}\lambda_{i}b_{i}a_{i}^\mathsf{T})x+\sum_{i=1}^{m}(\mu-\lambda_{i}-\nu_{i})\xi_{i}+\sum_{i=1}^{m}\lambda_{i}.
\end{align*}

对x,\zeta求偏导得到


\begin{align*}
\frac{\partial L}{\partial x}&=x-\sum_{i=1}^m\lambda_ib_ia_i^\mathsf{T}=0\notag\\
\frac{\partial L}{\partial \zeta_i}&=\mu-\lambda_i-\nu_i=0\notag
\end{align*}

进一步得到


\begin{align*}
x=\sum_{i=1}^m\lambda_ib_ia_i^\mathsf{T}\\
\mu-\lambda_i-\nu_i=0
\end{align*}

代入拉格朗日函数得到


\begin{align*}
    L(x,\zeta,\lambda,nu)=-\frac{1}{2}\Vert \sum_{i=1}^m \lambda_ib_ia_i\Vert_2^2+\sum_{i=1}^m\lambda_i
\end{align*}

所以对偶问题为


\begin{align*}
    \max \quad &-\frac{1}{2}\Vert \sum_{i=1}^m \lambda_ib_ia_i\Vert_2^2+\sum_{i=1}^m\lambda_i,\\
    \text{s.t.}\quad &\lambda_i\geq 0, i=1,2,\cdots,m,\\
    &\mu-\lambda_i-\nu_i=0, i=1,2,\cdots,m,\\
    &\nu_i\geq 0, i=1,2,\cdots,m.
\end{align*}

消去\nu_i得到


\begin{align*}
    \max \quad &-\frac{1}{2}\Vert \sum_{i=1}^m \lambda_ib_ia_i\Vert_2^2+\sum_{i=1}^m\lambda_i,\\
    \text{s.t.}\quad &\lambda_i\geq 0, i=1,2,\cdots,m,\\
    &\mu-\lambda_i\geq 0, i=1,2,\cdots,m.
\end{align*}

证明题

凸优化问题的可行域、解集都是凸集
弱对偶原理
Slater条件满足时，KKT条件是凸问题全局最优解的一阶充要条件
- Slater条件说明强对偶性成立，且最优化可以达到
- 必要性，充要性
交替方向乘子法的收敛性准则

【凸优化问题的可行域、解集都是凸集】

标准形式的凸优化问题：


\begin{align}
\min _{x \in D} \quad & f(x) \\
\text { s.t. } \quad & g_i(x) \leq 0, \quad i=1, \ldots, m \\
& A x=b
\end{align}

目标函数f、不等式约束条件g_i都是凸函数，必须是Ax=b
定义域D=\text{dom }f\cap (\cap_{i=1}^m\text{dom }g_i)通常省略
可行域为X=D\cap\{x\mid g_i(x)\leq 0,i=1,2,\cdots,m,Ax=b\}

凸优化问题的可行域为凸集

证明：

凸函数的定义域为凸集，任意多凸集的交为凸集\Rightarrow 定义域D是凸集.

利用凸函数的定义可以得到\{x\mid g_i(x)\leq 0\}为凸集.

线性方程组的解集\{x\mid Ax=b\}为凸集，于是证明X为凸集.
（在凸优化问题中，g_i(x)被要求是凸函数）

凸优化问题的解集是凸集

若X_\mathsf{opt}为下面凸优化问题的解集，即


\begin{aligned}
&X_\mathsf{opt}=\operatorname*{argmin}_x ~f(x)\\
\text{s.t}\quad &g_i(x)\leq 0,\quad i=1,...,m,\\
&Ax=b
\end{aligned}

证明：X_\mathsf{opt}是凸集

首先来看凸集的定义：

一个集合C是凸集，当且仅当对于任意x,y\in C和t\in[0,1]，点z=tx+(1-t)y\in C

若x,y是凸优化问题的解，则f(x)=f(y)=f^*。
对于任意的0\leq t\leq 1，设z=tx+(1-t)y，有
- g_i(tx+(1-t)y)\leq tg_i(x)+(1-t)g_i(y)\leq 0 （约束条件g_i(z)\leq 0）
- A(tx+(1-t)y)=tAx+(1-t)Ay=b （线性约束Az=b）
- f(t x+(1-t)y)\le t f(x)+(1-t)f(y)=f^{*}
（由上面三条可得，点z=tx+(1-t)y既满足所有约束条件，又达到目标函数的最优值f^*，所以z也是解）
由于对于任意x,y\in X_\mathsf{opt}和t\in [0,1]，都能证明z=tx+(1-t)y\in X_\mathsf{opt}，因此X_\mathsf{opt}是一个凸集
（CarryOS:所以tx+(1-t)y也是凸优化问题的解）

【弱对偶原理】

定理（弱对偶原理）

若\lambda\geq 0，则g(\lambda,\nu)\leq p^*.

证明：

首先来看L(x,\lambda,\nu)的性质。对于任意的x\in\mathcal{X}（满足原问题约束的x）有：


L(x,\lambda,\nu)=f_{0}(x)+\sum_{i}\lambda_{i}g_{i}(x)+\nu^{T}h(x).

因为\lambda_i\geq 0,g_i(x)\leq 0，所以\lambda_ig_i(x)\leq 0，又\nu^\mathsf{T}h(x)=0，所以


\color{blue}{L(x,\lambda, \nu)\leq f_0(x)}

(直观感受：通过引入约束条件的惩罚项，拉格朗日函数始终是原目标函数的“放松版”或下界，始终是一个较低的值。)

再来看对x取下确界inf。从定义可知


\color{green}{g(\lambda,\nu)=\operatorname*{inf}_{x}L(x,\lambda,\nu),}

因此对于任意的x\in\mathcal{X}有：


g(\lambda,\nu)\le L(x,\lambda,\nu).

若\tilde{x}\in \mathcal{X}且\lambda \geq 0，则


\color{green}{g(\lambda,\nu)=\inf_x L(x,\lambda,\nu)} \color{black}{\leq}  \color{blue}{L(\tilde{x},\lambda,\nu)\leq f_0(\tilde{x})}

对\tilde{x}取下界（对所有可能的\tilde{x}取下确界）得


g(\lambda,\nu)\leq \inf_{\tilde{x}\in\mathcal{X}} f_0(\tilde{x})=p^*

Slater条件满足时，KKT条件是凸问题全局最优解的一阶充要条件

Slater条件说明强对偶性成立，且最优化可以达到
必要性，充要性

【如果凸优化问题(5.6.1)满足 Slater条件，则强对偶原理成立】

证明：（太多了，我赌他不考，在书的P193-P195，定理5.12）

【必要性】

若强对偶性成立（比如Slater条件满足），x^*和\lambda^*,\nu^*分别是原始和对偶最优解，则有：


\begin{aligned}
f_{0}\left(x^{*}\right)=g\left(\lambda^{*}, \nu^{*}\right) & =\inf _{x} f_{0}(x)+\sum_{i=1}^{m} \lambda_{i}^{*} f_{i}(x)+\nu^{* T}(A x-b) \\
& \leq f_{0}\left(x^{*}\right)+\sum_{i=1}^{m} \lambda_{i}^{*} f_{i}\left(x^{*}\right)+\nu^{* T}\left(A x^{*}-b\right) \\
& \leq f_{0}\left(x^{*}\right)
\end{aligned}

最后一个不等式由弱对偶原理得到. 故上面两个不等式都是等式

x^*极小化L(x,\lambda^*,\nu^*)，可得稳定性条件
\lambda_{i}^{*}f_{i}(x^{*})=0,i=1,\cdot\cdot\cdot\cdot,m，可得互补松弛条件
- 互补松弛体现在下面的式子


  \lambda_{i}^{*}>0\Longrightarrow f_{i}(x^{*})=0,\qquad f_{i}(x^{*})<0\Longrightarrow\lambda_{i}^{*}=0

情况 1：如果 f_i(x^∗)=0（约束活跃）：
- 这说明约束 f_i(x^*)\leq 0 对最优解起到了直接作用，即这个约束将x^*限制在它的边界上。此时，\lambda_i^*\gt 0，表示这个约束对优化的贡献（或者“约束作用力”）是正的。
情况 2：如果 f_i(x^*)\lt 0（约束不活跃）：
- 这说明约束f_i(x^*)\leq 0附近并未限制优化过程，约束是“松弛”的，即f_i(x) 没有紧逼边界。此时，\lambda_i^* = 0，表示这个约束对最优解没有直接影响，也无需在优化过程中参与。
(注：对于一般的约束优化问题, KKT条件也是局部最优解的必要条件.)

【充分性】

设存在(\bar{x},\bar{\lambda},\bar{\nu})满足KKT条件，考虑凸优化问题的拉格朗日函数


  L(x,\lambda,\nu)=f_{0}(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\nu^{T}(A x-b).

固定\lambda=\bar\lambda,\nu=\bar\nu，注意到\bar{\lambda}_{i}\ge0,i=1,\cdots,m以及\bar{\nu}^{T}(A x-b)是仿射函数，于是L(x,\bar\lambda,\bar{\nu})是关于x的凸函数
由凸函数全局最优点的一阶充要性可知,此时\bar x就是L(x,\bar\lambda,\bar{\nu})的全局极小点.根据拉格朗日对偶函数的定义，可得


  L(\bar{x},\bar{\lambda},\bar{\nu})=\operatorname*{inf}_{x\in\mathcal{D}}L(x,\bar{\lambda},\bar{\nu})=g(\bar{\lambda},\bar{\nu}).

（凸函数的一阶最优值条件）对于一个凸函数f(x)，如果x^*是其定义域内的一个点，并且满足
\nabla f(x^*)=0
则x^*是f(x)的全局最优解

根据原始可行性条件A\bar{x}=b以及互补松弛条件\bar{\lambda_i}f_i(\bar{x})=0，可得


  L(\bar{x},\bar{\lambda},\bar{\nu})=f_{0}(\bar{x})+0+0=f_{0}(\bar{x}).

根据弱对偶原理，得到


  L(\bar{x},\bar{\lambda},\bar{\nu})=f_{0}(\bar{x})\ge p^{*}\ge d^{*}\ge g(\bar{\lambda},\bar{\nu})=L(\bar{x},\bar{\lambda},\bar{\nu})\Rightarrow p^{*}=d^{*}.

故\bar{x}和\bar\lambda,\bar\nu分别是原始问题和对偶问题的最优解.

总结：

必要性：如果 x^* 是原问题的最优解，且问题满足 强对偶性（例如 Slater 条件），那么 x^* 必须满足 KKT 条件。

充分性：如果 x^*,\lambda^*,\nu^* 满足 KKT 条件，且问题是 凸优化问题，那么 x^* 一定是原问题的全局最优解。

【交替方向乘子法的收敛性准则】

（我不知道在哪里）

ADMM收敛性准则：

检测前述两个残差r^k,s^k是否充分小：


  0\approx||r^{k}||=||A_{1}x_{1}^{k}+A_{2}x_{2}^{k}-b|| \qquad \text{（原始可行性）}\\
  0\approx||s^{k}||=||A_{1}^{\mathrm{T}}A_{2}(x_{2}^{k-1}-x_{2}^{k})||\qquad \text{（对偶可行性）}

致谢

感谢楠姐指出的两处错误（定义域和可行域的错误以及标注错误）
感谢杜哥作为第一个读者的精神支持

CarryNotKarry

来自湖南长沙

最优化期末复习

最优化考试内容

期末考试题型

简答题

计算题

证明题

简答题

计算题（我的作业）

最优化理论与方法作业 1

练习2.6:

练习2.7

练习2.12

最优化理论与方法作业 2

一、计算次梯度

二、线性规划

三、复合函数计算导数

最优化理论与方法作业 3

一、梯度法的精确步长

最优化理论与方法作业 4

一、对偶问题

二、KKT点

三、支持向量机

证明题

致谢

发表回复取消回复

分类

归档

最优化考试内容

期末考试题型

简答题

计算题

证明题

简答题

计算题（我的作业）

最优化理论与方法 作业 1

练习2.6:

练习2.7

练习2.12

最优化理论与方法 作业 2

一、计算次梯度

二、线性规划

三、复合函数计算导数

最优化理论与方法 作业 3

一、梯度法的精确步长

最优化理论与方法 作业 4

一、对偶问题

二、KKT点

三、支持向量机

证明题

致谢

发表回复 取消回复

分类

归档

最优化理论与方法作业 1

最优化理论与方法作业 2

最优化理论与方法作业 3

最优化理论与方法作业 4

发表回复取消回复