第十四届蓝桥杯有感+部分题解

试题点此下载 下面在线查看试题
第十四届蓝桥杯大赛软件赛省赛_CA

写在前面

4.8号9:00～13:00进行的蓝桥杯省赛真是累死了，周五又帮忙分发食品，又有高数考试，还作为能源二队队长出战最后2:1战胜经管二队，然后... 周六早上都不想起床... 可是生活所迫.. 考试的时候都想睡着了

怎么说呢，跟每年都差不多，一开始把填空题写完，不出意外，肯定至少错一个；然后C、D两题看看能不能写正解.. 不出意外是真的暴力杯，然后打满了暴力，不知道最后有多少分，希望能有一个省一打进国赛..

B.有奖问答

题面

小蓝正在参与一个现场问答的节目。活动中一共有30道题目，每题只有答对和答错两种情况，每答对一题得 10 分，答错一题分数归零。

小蓝可以在任意时刻结束答题并获得目前分数对应的奖项，之后不能再答任何题目。最高奖项需要 100 分，所以到达 100 分时小蓝会直接停止答题。

已知小蓝最终实际获得了 70 分对应的奖项，请问小蓝所有可能的答题情况有多少种?

思路

这题我错了，是一个4开头的7位数，我标黑的地方是我觉得更重要的地方，较为重要的例如“归零”和“停止答题”等大家都看得见，需要注意“在任一时刻结束答题”这个地方，也就是说我可以在中途拿到70分就结束，也可以拿到70分之后还继续答题...，我没有看清楚中途可以退出的答案...

代码

inline void dfs(int x, int r) {
    if (r == 70) ans++;// 不要return 还可以继续
    if (r == 100 || x == 30) return;//停止
    dfs(x + 1, r + 10);// 答对
    dfs(x + 1, 0);// 答错
}

inline void Case_Test() {
    dfs(0, 0);
    cout << ans << endl;
}

输出是：8335366，本地用时：4.53897s

C.平方差

题面

询问[L,R]中有多少个数字能被两个平方差表示。

思路

这个题在前几届校赛考过，可以从奇偶性判断，也就是$x=(a-b)\times (a+b)$，其中$(a-b)$和$(a+b)$的奇偶性相同，最后可以推出来模2为0但是模4不为0的数不可以，也就是2、6、10、14、18等不可以。

代码

可以写一个函数表示从1到x的有多少个数字可以，然后对于[L,R]就只要cout << f(R) - f(L - 1)即可

D.更小的数

题面

给你一个字符串其中只包括0到9，然后可以让其中一段翻转一次，求让新的数字比原数字小的方案有多少种，可以有前导零。

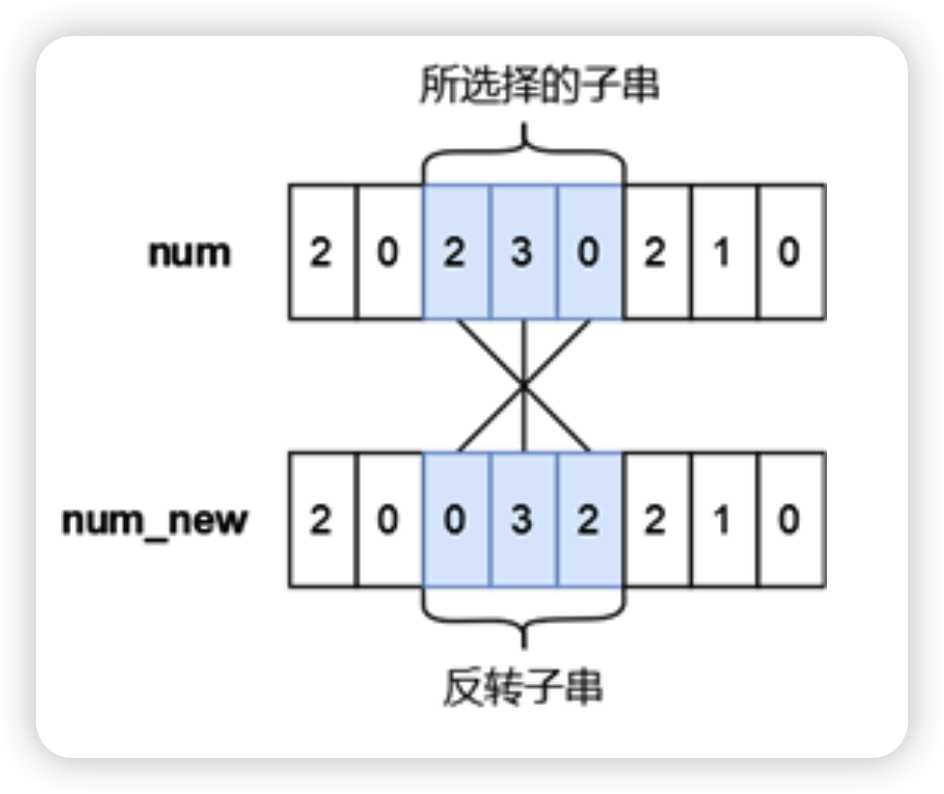
新数字200032210小于原数字20230210

思路

首先其实我们只需要观察到对于其中一段[L,R]如果l=s[L]大于r=s[R]的话，这样逆转过来的话在左侧的r要小于翻转后在右侧的l，例如上图中的s[L]='2'以及s[R]='0'，对于翻转之后，高位的'0'比原来的'2'要小，按照比较的方式肯定要小，符合条件。

然后想到如果相等呢？那么就需要比较下一位也就是s[L+1]以及s[R-1]，同样的方式，如果s[L+1]>s[R-1]的话，那么就也可以，例如2312全翻转之后是2132，原因就是第二位的3比第三位的1要大。

然后想到如果还相等呢？那么还得往下看...

所以我们就可以想到类似于区间DP的方法，也就是说每次由小的区间推向大的区间，我这里定义ok[l][r]表示如果翻转区间[l,r]是否可以，如果可以则是true。那么递推式就是:

• 如果s[l]>s[r]，那么更好，ok[l][r] = true;
• 否则判断s[l] == s[r]，如果是则需要看里面的ok[l+1][r-1]，从之前继承而来，而ok[l+1][r-1]又可以从之前判断...

然后想到如果s[l]<s[r]呢？不用看，这个区间肯定不行的。

这里不需要判断l>r的情况，因为肯定是false。然后枚举统计true的个数，时间复杂度是$O(n^2)$。

代码

int ok[N][N];
inline void Case_Test() {
    cin >> s;
    n = s.size();
    for (int d = 1; d < n; d++) {// 枚举区间间隔，保证每次处理完小区间
        for (int l = 0; l + d < n; l++) {// 枚举左端点
            int r = l + d;// 右断点
            if (s[l] > s[r]) ok[l][r] = 1;// 这个区间肯定可以
            else if (s[l] == s[r]) ok[l][r] = ok[l + 1][r - 1];// 看里面的区间
            ans += ok[l][r];
        }
    }
    cout << ans;
}

E.颜色平衡树（Dfs序+莫队 / 启发式合并）

题意

给定一棵树，结点由$1$至$n$编号，其中结点$1$是树根。树的每个点有一个颜色$C_i$。

如果一棵树中存在的每种颜色的结点个数都相同，则我们称它是一颗颜色平衡树。

求出这棵树中有多少个子树是颜色平衡树。

思路

考前还在看分块莫队，还在思考这场怎么用不上，这个题的时候也一闪而过了但是没有想到怎么查询，所以... 所以总结一句话——“看到子树问题第一个想到Dfs序”，这样把每个点的入栈顺序展开之后，对于每一个结点$i$就可以获得一个区间$[L,R]$其中$L=\text{in}[i],R=\text{out}[i]$，这样只需要查询区间$[L,R]$中间每种颜色的结点个数是否相同。

前置知识（不会的人建议看！）
Dfs序可以参考这篇文章：DFS序 - CarryNotKarry
然后莫队可以参考这篇文章：『莫队算法』- CarryNotKarry的博客-CSDN博客，这里面有些例题，也有一些统计颜色类似的题，以及莫队的一些优化等。

然后来拆分一下代码讲解：
这里还是一样需要一个结构体，不过只需要l,r来计算需要统计子树的区间，然后排序就是普通的cmp即可，然后在读入之后进行遍历处理出in[i],out[i]。
这里注意Dfs序只需要in[i]=++dfn然后out[i]=dfn即可，之前写out[i]=++dfn这个应该叫欧拉序，而且这样会使得我展开的新节点多一倍之多，这样在莫队区间移动中del(),add()大大耗时间，这样导致tle，这里需要注意！

inline void dfs(int x) {
    in[x] = ++dfn;
    for (int i = head[x]; i; i = edge[i].next) {
        int y = edge[i].to;
        dfs(y);
    }
    out[x] = dfn;//不需要++dfn
}

输出一下结点以及它的in[i]和out[i]，可以看出如下：

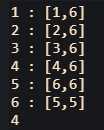
（样例）输出结点对于的in[i]以及out[i]查看

例如这时候需要计算以$2$为根的子树，就只需要查询区间$[2,6]$之间的颜色个数是否相同。后面就是对区间进行排序然后莫队正常操作，最后重要的就是如何查看当前状态是否是满足条件的状态，也就是add()和del()操作以及如何统计答案。

我们用一个unordered_map来记录——颜色出现的个数的次数（频率），举个例子：颜色2出现1次，颜色3出现5次，那么这个时候mp[1]=1,mp[5]=1，我这里不管颜色，只管颜色出现的个数出现了多少次；例如颜色2出现1次，颜色3出现5次，颜色4出现1次，那么这个时候mp[1]=2,mp[5]=1，因为出现1次一共有2种颜色。

为什么这样子呢？因为我们需要用到mp.size()，如果mp.size()==1这说明所有颜色出现的次数都是一样的，比如颜色2出现5次，颜色3出现5次，颜色4出现5次，这个时候是mp[5]=3，出现5次的颜色一共有3个（一定要理解！）
还需要注意，如果颜色次数变为0就需要在mp中擦除，用mp.erase()去掉，不需要占用mp的空间导致mp.size()出错。

然后就是add()和del()的维护，这里当然需要用一个数组num[i]来计算颜色i在当前状态出现的次数，当然，将Dfs序按照1..n进行展开对应的不一定是原来的，也就重新需要一个数组newcol来存当前dfn的结点对应的颜色（例如上图的5号结点实际上是在dfn=6的位置上）。

只需要注意先后顺序，在两个函数中步骤大致一样，以del举例：首先需要将原来在mp中贡献出现次数的频率-1，只要有减法就需要判断是否为0擦除，然后在num中更新颜色的值，然后如果还有就对mp重新产生贡献。

举例细说的话就是，例如颜色3出现了5次，颜色2也是5次，这个时候mp[5]=2，现在要删掉这个结点颜色对应的是3，所以需要mp[5]--，然后num[3]更新为4，发现不为0，则又对mp产生贡献，则mp[4]=1，这个时候mp里村的值是mp[4]=1,mp[5]=1，是不满足条件的，每次只需要$\text{O}(1)$判断是否mp.size()==1即可。

inline void del(int x) {
    int c = newcol[x];
    mp[num[c]]--;// 该颜色在原来的贡献值-1
    if (mp[num[c]] == 0) {
        mp.erase(num[c]);
    }
    num[c]--;
    if (num[c]) mp[num[c]]++;
}
inline void add(int x) {
    int c = newcol[x];
    if (num[c]) mp[num[c]]--;// 如果有，要减去原来对mp产生的贡献
    if (mp[num[c]] == 0) {
        mp.erase(num[c]);
    }
    num[c]++;
    mp[num[c]]++;
}

启发式合并请看脱老师博客：树上启发式合并（DSU on Tree）总结 :: Thallium54 (tgc54.com)

代码

最后代码如下：

const int N = 200000+7;
int col[N], f, n, ans;
struct node {
    int to, next;
}edge[N];
int head[N], cnt, num[N];
inline void add(int x, int to) {
    edge[++cnt].to = to;
    edge[cnt].next = head[x];
    head[x] = cnt;
}
int dfn, in[N], out[N], belong[N], newcol[N];
unordered_map<int, int> mp;
inline void dfs(int x) {
    in[x] = ++dfn;
    for (int i = head[x]; i; i = edge[i].next) {
        int y = edge[i].to;
        dfs(y);
    }
    out[x] = dfn;
}
struct mo {
    int l, r;
}q[N << 1];
inline bool cmp(const mo &a, const mo &b) {
    return belong[a.l] == belong[b.l] ? a.r < b.r : a.l < b.l;
}
inline void del(int x) {
    int c = newcol[x];
    mp[num[c]]--;
    if (mp[num[c]] == 0) {
        mp.erase(num[c]);
    }
    num[c]--;
    if (num[c]) mp[num[c]]++;
}
inline void add(int x) {
    int c = newcol[x];
    if (num[c]) mp[num[c]]--;
    if (mp[num[c]] == 0) {
        mp.erase(num[c]);
    }
    num[c]++;
    mp[num[c]]++;
}
inline void Case_Test() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> col[i] >> f;
        if (f) add(f, i);
    }
    dfs(1);
    for (int i = 1; i <= n; i++) {
        // cout << i << " : [" << in[i] << "," << out[i] << "]" << endl;
        q[i].l = in[i], q[i].r = out[i];
        newcol[in[i]] = col[i]; newcol[out[i]] = col[i];// dfn改变原来位置，需要用newcol
    }
    int sq = sqrt(dfn);// 根号
    for (int i = 1; i <= dfn; i++) {
        belong[i] = (i - 1) / sq + 1;// 预处理
    }
    sort(q + 1, q + 1 + n, cmp);// 查询区间排序
    int l = 1, r = 0;// 莫队初始化
    for (int i = 1; i <= n; i++) {
        while (l < q[i].l) del(l++);
        while (l > q[i].l) add(--l);
        while (r < q[i].r) add(++r);
        while (r > q[i].r) del(r--);// 莫队四种转移
        if (mp.size() == 1) ans++;
    }
    cout << ans;
}

G.网络稳定性

待补，我觉得生成树+LCA可以做