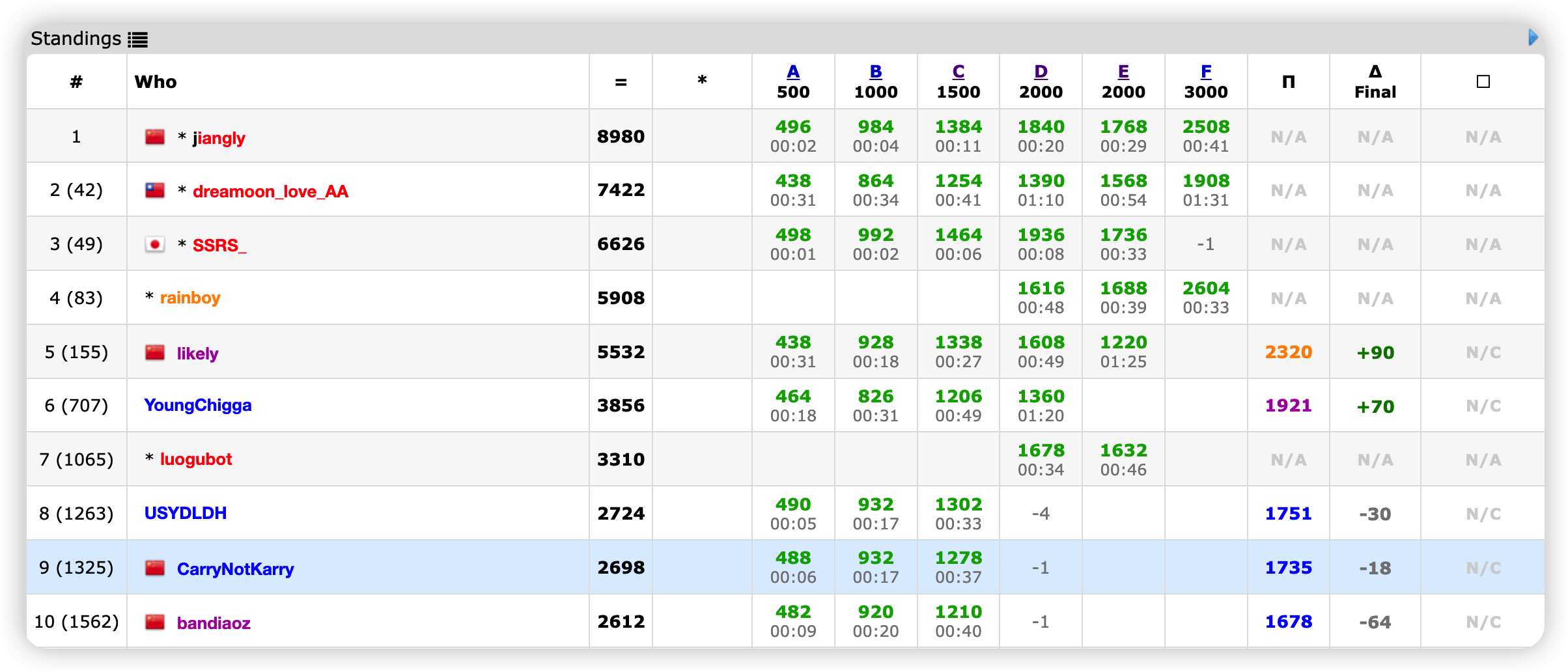
比赛链接:Codeforces Round #818 (Div. 2)
D读假题,演了一个多小时。
A.Madoka and Strange Thoughts(800)
inline void Case_Test()
{
cin>>n;
ans = (n/3)*5+(n/2-n/3)*3+(n-n/2);
cout<<ans<<endl;
}
B. Madoka and Underground Competitions(模拟|1100)
题意:给你$\rm n,k,r,c$,你需要构造一个$n\times n$的二维矩阵$\rm ans$,每连续的$\rm k$个都需要含有至少一个'X',并且ans[r][c]='X',请问使用最少的'X'构造的答案是什么。($\rm n$是$\rm k$的倍数)
思路:最少肯定是每$k$个只用一个'X',我是小的方阵也就是$k\times k$,构造对角线的'X',然后需要修改的就单独两行换就好了
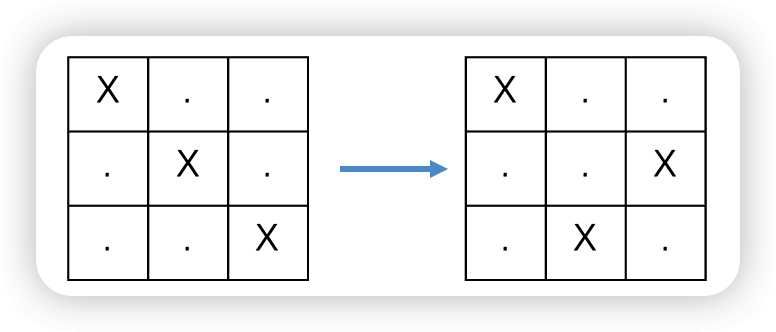
先对角线,如果哪里需要单独两行改
然后因为n是k的倍数,所以只需要拿这个小的$k\times k$去填补就好:
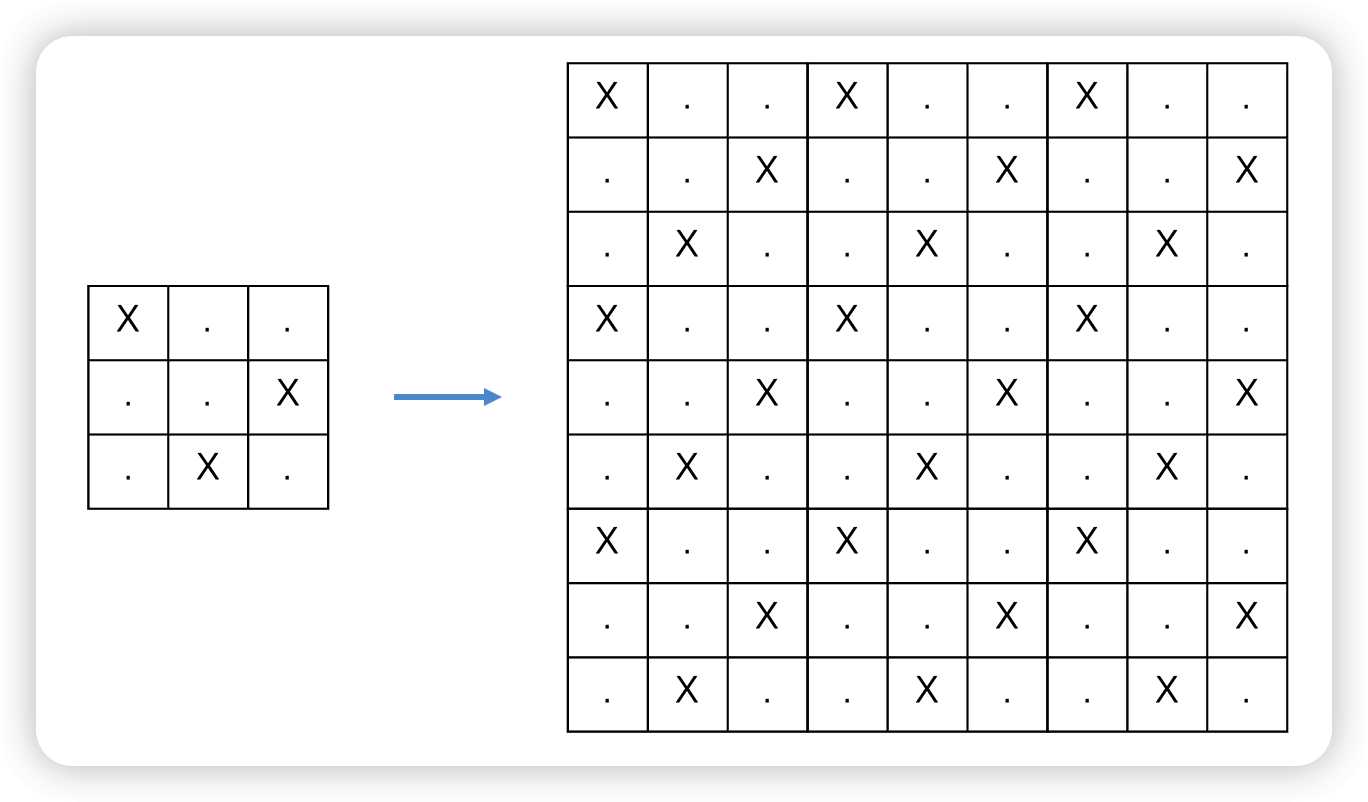
复制
代码:
char ans[N][N],ch[N][N];
inline void Case_Test()
{
cin>>n>>k>>r>>c;
r = (r-1)%k+1, c = (c-1)%k+1;
m = n/k;
for (int i=1;i<=k;i++)
for (int j=1;j<=k;j++)
if (i==j)
ch[i][i] = 'X';
else
ch[i][j] = '.';
ch[c][c] = '.';
ch[r][c] = 'X';
ch[r][r] = '.';
ch[c][r] = 'X';//两行
for (int i=1;i<=m;i++)
for (int j=1;j<=m;j++)
{
int rr = (i-1)*k, cc = (j-1)*k;
for (int t=1;t<=k;t++)
for (int p=1;p<=k;p++)
ans[rr+t][cc+p] = ch[t][p];//填补
}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++)
cout<<ans[i][j];
cout<<endl;
}
}
C. Madoka and Formal Statement
题意:你有$a$数组以及$b$数组,请问是否可以通过以下操作使得$a$变成$b$。
- 选择一个$a[i]$,如果$a[i]\leq a[i+1]$就可以使得$a[i]:=a[i]+1$。特别的,这是一个环,也就是$n$的下一个是$1$,
思路:
- 如果:$a[i]>b[i]$,因为不能降低,所以无解
- 如果:$a[i]=b[i]$,这时候不需要改变
- 如果:$a[i]<b[i]$,则$a[i+1]$至少应该加到$a[i]-1$,如果这个值比$b[i+1]$大也无解。
代码:
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) cin>>b[i];
for (int i=1;i<=n;i++)
if (a[i]>b[i]) {NO;return;}
for (int i=1;i<=n;i++)
{
if (a[i]==b[i]) continue;
y = i%n+1;
if (b[i]-1>b[y]) {NO;return;}
}
YES;
}
D. Madoka and The Corruption Scheme(组合数学)1900
题意:有一个 $n$ 轮淘汰赛组成的比赛,共有 $2 ^{n}$ 位玩家参赛,玩家们的晋级路线形成一棵二叉树。 Madoka 想要让编号尽可能小的选手获胜,于是预先安排好了每场比赛到底是左子树的玩家赢还是右子树的玩家赢。现在你可以改变至多 $k$ 场比赛的比赛结果来尽可能干扰最终的冠军人选,使得最后冠军编号尽可能大。 Madoka 在安排比赛的时候考虑到了你有着改变比赛结果的能力。问改变比赛结果后,最小的可能获胜的选手编号对 $10^9+7$ 取模后的结果。
思路:这个题一开始的题意读错了..导致一直写错,知道最后才发现不是那个意思..
一开始已经有一个树,然后我有$k$次改变的能力,我假设能改变$x$个人,这$x$里面就有小的,也有最大的,然后Madoka就可以事先安排好这些数字,他想让无论我怎么做,最后赢得最小。
那么就是让这$x$个数分别安排为$1,2,\cdots ,x$,这样我最大只能得到$x$,这是所有情况里面最小的时候了。
假设树都是左边赢,右边输,然后叶子顺序排列,可以得到:(以n=4,k=1)
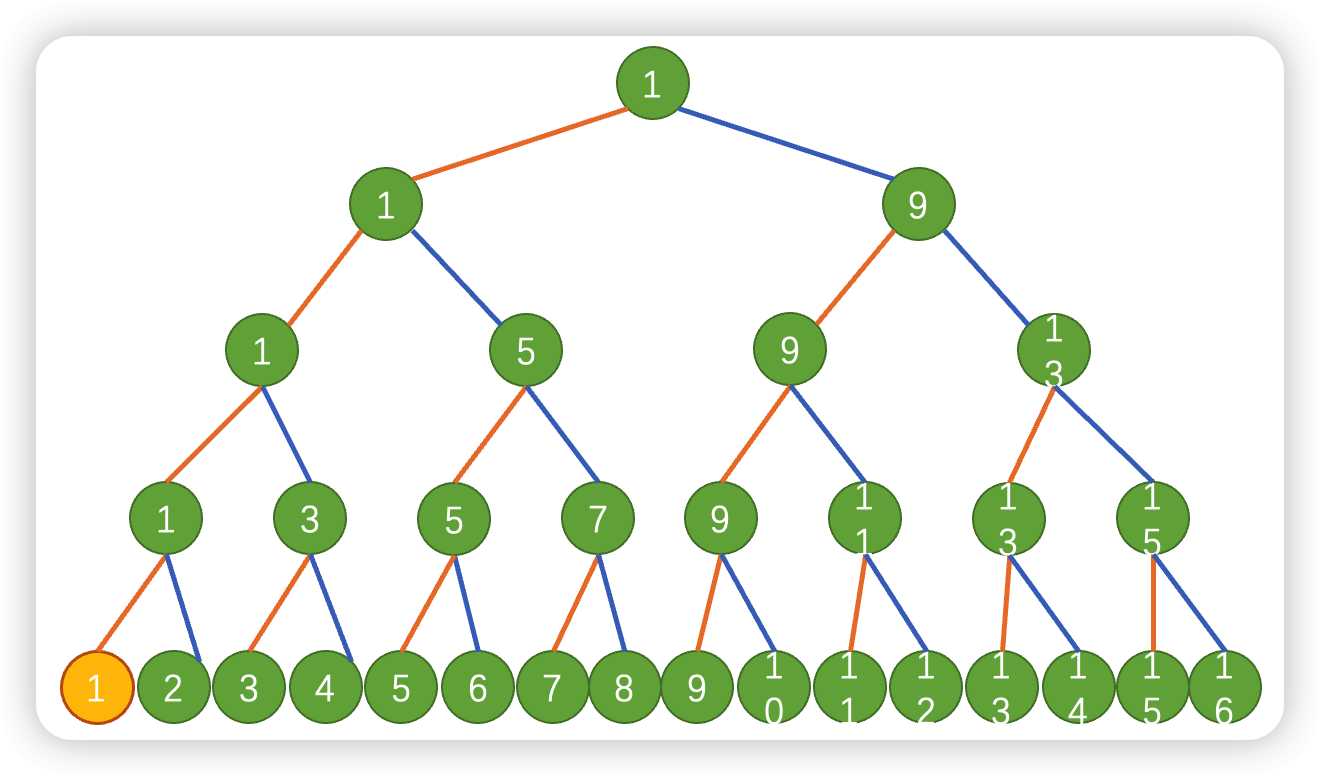
n=4的满二叉树
可以看出最后的$1$胜出是一直左下角的那个,那么我这时候改变一次,比如我想让$2$赢:
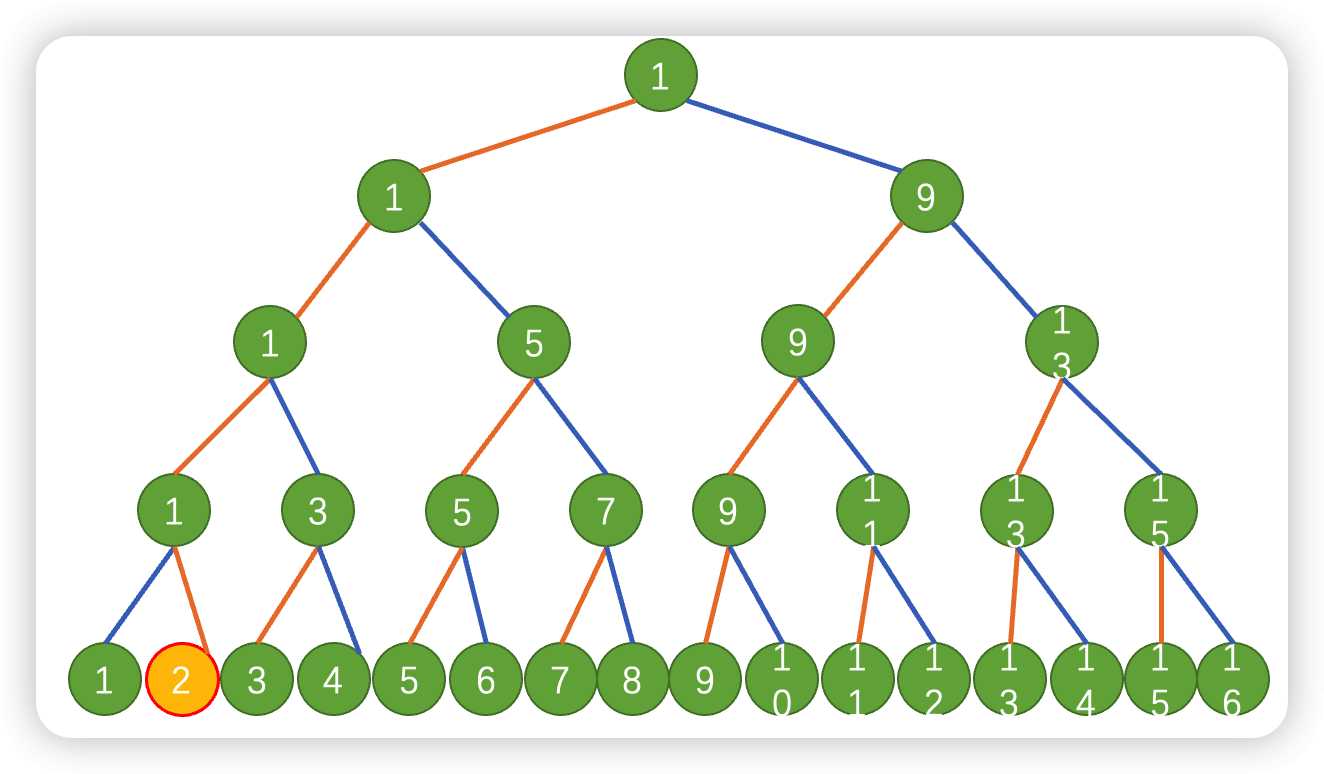
左下角让2赢
那么我改变一次所有能赢的选手有:
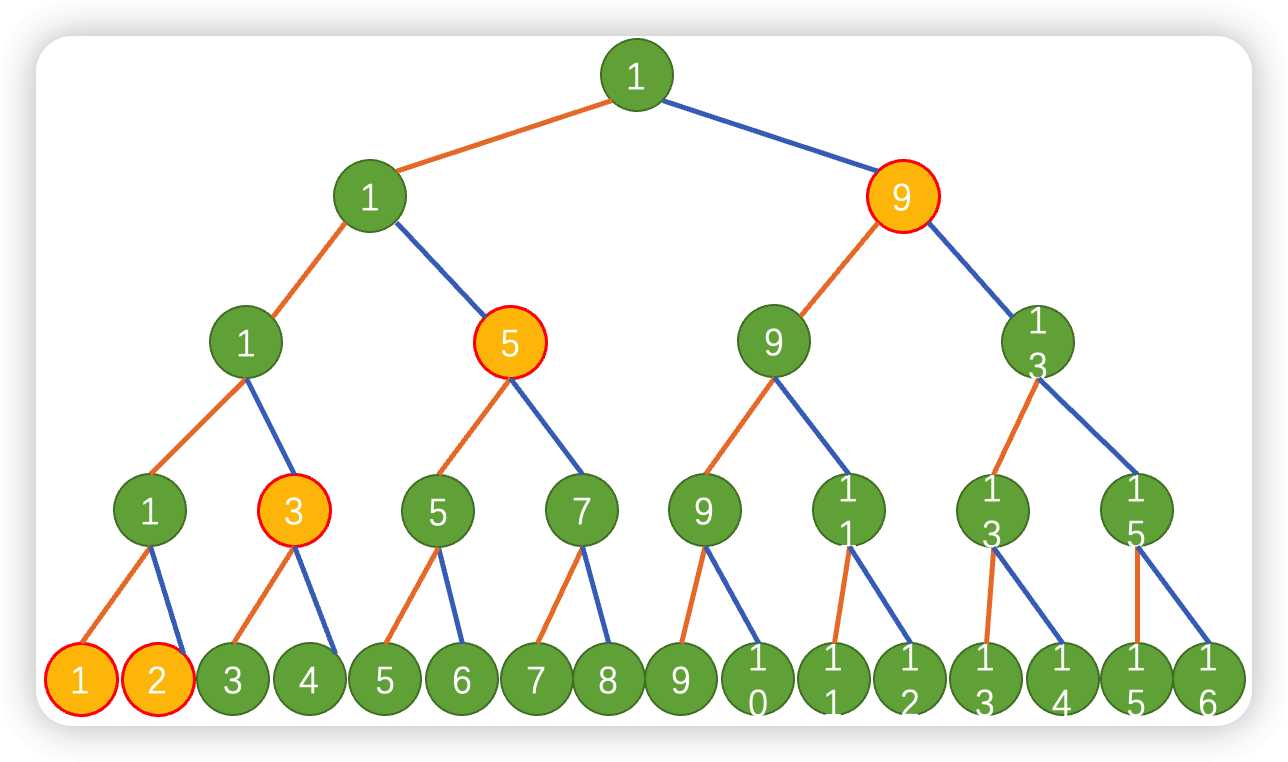
1是因为我随便改别的无关紧要的地方,他就能赢
我们再来看如何计算,我们全用二进制表示,1所在的位置是0000,9所在的位置是1000,2所在的位置是0001,3所在的位置是0010,5所在的位置是0100。
所以这个二进制的意义就是:只看1的个数,如果有x个1则表示这一个赢还需要x次改变。
那么具体是哪些改变呢?这个时候就是组合数学的知识点了。
首先我们需要k=min(k,n),因为如果k>=n所有的点都可以成为胜利者,所以剩下的没有必要了。
然后答案就是:
$$
\Sigma_{i=1}^kC(n,i)
$$
代码:
inline void Case_Test()
{
init();
cin>>n>>k;
k = min(k,n);
for (int i=0;i<=k;i++)
ans = (ans + C(n,i))%mod;
cout<<ans;
}
E. Madoka and The Best University(欧拉函数)2200
题意:给你$n$,计算$\Sigma \rm lcm(c,\gcd (a,b)),\ a+b+c=n$
思路:
我们可以枚举gcd,令$g=\gcd(a,b)$,则$a,b$都是$g$的倍数,有$a=k_1\times g,\ b=k_2\times g$,有$a+b=(k_1+k_2)\times g=k,\quad k=(k_1+k_2)\times g$。
此时$c=n-a-b=n-k$,$\gcd(a,b)$的每次贡献就可以跟$c$进行计算值,那么贡献多少次呢?也就是有多少个这样的$a,b$呢?
可以从上面得出来,$a,b$与$k_1,k_2$对应的,那么也跟$k$有关,有$k_1+k_2=\frac{a+b}{g}=\frac{k}{g}$.
所以现在要确定$k_1,k_2$的个数。现在因为$\gcd(a,b)=g$,那么一定有$gcd(k_1,k_2)=1$互质,又因为$k_2=\frac{k}{g}-k_1$,所以有
$$
\gcd(k_1,k_2)=\gcd(k_1,\frac{k}{g}-k_1)=\gcd(k_1,\frac{k}{g})=1
$$
也就是问,有多少个$k_1$与$\frac{k}{g}$互质,这个就是欧拉函数的定义,预处理之后直接phi[k/g]即可。
代码:
int phi[N];
void init(int n = N-2)
{
for (int i = 1; i <= n; i++)
phi[i] = i;
for (int i = 2; i <= n; i++)
if (phi[i] == i)
for (int j = i; j <= n; j += i)
phi[j] = phi[j] / i * (i - 1);
}
inline void Case_Test()
{
cin>>n;
for (int g = 1; g <= n; g++)
{
for (int k = 2*g; k < n; k+=g)//枚举k
{
ans = (ans + lcm((n-k),g) * phi[k/g])%mod;
}
}
cout<<ans;
}