比赛链接:Dashboard - Codeforces Round #805 (Div. 3) - Codeforces
这波偷偷拿小小号,估计能上400+分吧,没有做出G题...太菜了,我估摸着这回G题得有2000分?
周中没有几场,这场搞到唯一一天假可累死我了!下午还有robocom...
这场前几题简直是STL专场..
这场重点在EFG题。
A. Round Down the Price(模拟)
直接按照题意最高位-1即可,也可以用字符串。我这里是写一个函数找有多少位,比如有3位就减去100.
参考代码:
inline int calc(int x)
{
int res = 1;
while (x>=10)
{
x/=10;
res*=10;
}
return res;
}//找有多少位数字
inline void Case_Test()
{
cin>>x;
cout<<x-calc(x)<<endl;
}
B. Polycarp Writes a String from Memory(模拟)
按照题意模拟,我用一个set来存,如果size==3并且接下来一个数不在set里面,那么就清空并计数。
参考代码:
inline void Case_Test()
{
cin>>s;
n = s.size();
set<char> st;//用来存放出现的字符是什么(不超过三个)
ans = 1;
for (int i=0;i<n;i++)
{
if (st.size()==3&&st.find(s[i])==st.end())//如果正好为3个并且在set中没有出现,需要清空计数
{
ans++;//计数
st.clear();//情况
st.insert(s[i]);//当前这个算上去
}
if (st.find(s[i])==st.end())
st.insert(s[i]);//当前没出现,需要加上
}
cout<<ans<<endl;
}
C. Train and Queries(模拟)
每次对于x,y寻找第一个位置pos,然后找y中是否有pos之后的数。我用的set容器,然后因为数字很大所以用了离散化。
map<int,int> mp;
vector<int> v[N];
set<int> st[N];
inline void Case_Test()
{
cin>>n>>m;
mp.clear();cnt = 0;
for (int i=1;i<=n;i++)
{
cin>>x;
if (mp.find(x)==mp.end())
mp[x]=++cnt;
//v[mp[x]].push_back(i);
st[mp[x]].insert(i);
}
while (m--)
{
cin>>x>>y;
if (mp.find(x)==mp.end()||mp.find(y)==mp.end())
{
cout<<"NO"<<endl;
continue;
}
int pos = *st[mp[x]].begin();
if (st[mp[y]].lower_bound(pos)==st[mp[y]].end())
{
cout<<"NO"<<endl;
continue;
}
cout<<"YES"<<endl;
}
for (int i=1;i<=cnt;i++)
st[i].clear();
}
D. Not a Cheap String(贪心)
sort+排序,每次减最大的就行。
参考代码:
struct node
{
char c;
int id;
}ch[N];
inline void Case_Test()
{
cin>>s>>p;
n = s.size();
s = '#'+s;
int sum = 0;
for (int i=1;i<=n;i++)
{
vis[i] = 1;
ch[i].c = s[i];
ch[i].id = i;
sum += s[i]-'a'+1;
}
sort(ch+1,ch+n+1,[](node a,node b){return a.c>b.c;});//字符从大到小排序
int t = 1;
while (sum>p&&t<=n)
{
vis[ch[t].id] = 0;//删除
sum -= ch[t].c-'a'+1;//减去这个的贡献
t++;
}
for (int i=1;i<=n;i++)
if (vis[i]) cout<<s[i];
cout<<endl;
}
E. Split Into Two Sets(染色)
这个题可以用并查集(判奇数环),知乎上有些大佬是这样的,我写的很乱但是过了,wa是因为忘记删debug了。
(我赛时因为时间紧,过了就好,代码写的很丑...)
题意
给你$n$个牌九(有正反两个数字例如1 2),然后需要将其分为两类,每类中不能有一样的数字。
思路
我设了一个结构体
struct node
{
int x,y,id;//x,y为数字,id为下标
}a[N];
我的主要思想一开始判环,想了一会还是想到了当天robocom的第五题染色,那就建边染色吧。当前读入的是x,y,那么与之前的x,y'的关系是什么呢?说明这二者不能在同一集合,所以在染色中需要连边,同理,对于x',y也连起来。
ok = true;
for (int i=1;i<=n;i++)
{
cin>>x>>y;
col[i] = 0;
if (x==y) ok = false;//特判
a[i].x = x;
a[i].y = y;
a[i].id = i;
e[x].push_back({x,y,i});//建边
e[y].push_back({y,x,i});//只需要存{x,i}即可
}
然后就是对于每一个染色就好,小技巧就是col[y] = 3-col[x](应该很多都知道了)
我这里染色因为是分开写的,也就是对于每一个node都有一个id以及x,y对于x需要找其相连的边,对于y需要找相连的边。
代码
int col[N];
struct node
{
int x,y,id;
}a[N];
vector<node>e[N];
bool ok = true;
inline void dfs(node cur)
{
for (auto e:e[cur.y])
{
int y = e.y, id = e.id;
if (col[id] == 0)
{
col[id] = 3-col[cur.id];
dfs(a[id]);
}
else
{
if (id!=cur.id&&col[id] == col[cur.id])
{
ok = false;
return;
}
}
}
for (auto e:e[cur.x])
{
int y = e.y, id = e.id;
if (col[id] == 0)
{
col[id] = 3-col[cur.id];//对于目标结点染色
dfs(a[id]);//传入的是类型为node的结点
}
else
{
if (id!=cur.id&&col[id] == col[cur.id])//不能是自己且颜色相同
{
ok = false;
return;
}
}
}
}
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++) e[i].clear();
ok = true;
for (int i=1;i<=n;i++)
{
cin>>x>>y;
col[i] = 0;
if (x==y) ok = false;
a[i].x = x;
a[i].y = y;
a[i].id = i;
e[x].push_back({x,y,i});
e[y].push_back({y,x,i});
}
for (int i=1;i<=n;i++)
{
if (col[i]==0)//如果还没找过
{
col[i] = 1;
dfs(a[i]);
}
}
if (ok) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
F. Equate Multisets(贪心)
题意
给你一个长度为$n(1\leq n\leq 2\times 10^5)$的数组$a,b$,$a$数组不可移动,你用两种方式可以改变$b$数组,问是否可以变成$a$数组,方式为:
- 选择$b_i$使得$b_i = \left \lfloor \frac{b_i}{2} \right \rfloor $
- 选择$b_i$使得$b_i = b_i \times 2$
思路
这个题是abc254的EX(待补),不过那个题是求最小次数。Ex - Multiply or Divide by 2 (atcoder.jp)
这个题我认为跟前几天的2C很像:Codeforces Global Round 21 (C构造贪心,D分治ST表,E组合数学) - CarryNotKarry 中的C题。
虽然告诉你数组$a$不能动,但是因为$b$的操作是可以逆操作的(那篇博客也说了),所以我们可以修改 $a$:
对于一个$2$的倍数的$a_i$,我们可以一直除以2,例如现在$a_i=28$,那么除以二为$14$,是二的倍数,还可以除,变成$7$之后不变了。
for (int i=1;i<=n;i++)
{
cin>>x;
while (x%2==0) x/=2;
mp[x]++;
}
为什么可以这么做,假如原来有个数可以变成$28$,例如$14$或者$56$,他们同样也能变为$7$。如果是$57$呢?请往后看。
就这样我们都存放在了map里面,因为可能会有相同数字,就不用set了,接下来就是对$b$数组的处理,对于每一个$b_i$来说判断mp[b[i]]是否大于0,大于0说明有对应的$a$数组的数,所以就可以mp[b[i]]--,如果没有呢?那么就除以$2$.(这里不用考虑乘以$2$的事情,如果真的符合,$a$那边自己会除以$2$的,否则不可能相等)
for (int i=1;i<=n;i++)
{
cin>>x;
while (x&&mp[x]==0) x/=2;//一直除以二
if (mp[x]) mp[x]--;//如果是mp[x]>0出循环的 那么就--
else ok = false;
}
就这样下去即可
代码
inline void solve()
{
cin>>n;
map<int,int> mp;
for (int i=1;i<=n;i++)
{
cin>>x;
while (x%2==0) x/=2;
mp[x]++;
}
bool ok = true;
for (int i=1;i<=n;i++)
{
cin>>x;
while (x&&mp[x]==0) x/=2;
if (mp[x]) mp[x]--;
else ok = false;
}
if (ok) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
G2. Passable Paths (hard version)(LCA+DFS序)
题意
给你一颗有$n(1\leq 2\times 10^5)$个结点的树,并且有$q(1\leq q\leq 10^5)$次询问,一共最多询问$2\times 10^5$次。
每次询问一个总数$k$,然后有$k$个数字,问这$k$个点是否在同一路线上,也就是每条边只能够走一次并且走完所有的点,输出YES或者NO
思路
Codeforces Round #805 (Div. 3) E(染色) F(贪心) G(lca) - 知乎 (zhihu.com)
看大佬严格鸽补题的,内容大致与其一样,接下来是我的思考与理解(在大佬的基础上)。
首先比较重要的是DFS序,用$O(1)$的时间复杂度判断。
请见这一篇文章:DFS序 - CarryNotKarry
int in[N],out[N],dfn;
inline void dfs(int x,int fa)
{
in[x] = ++dfn;
for (int i=head[x];i;i=edge[i].next)
{
int y = edge[i].to;
if (y!=fa)
dfs(y,x);
}
out[x] = dfn;
}
inline bool isp(int u,int v)
{
return in[u]<=in[v] && out[v]<=out[u];//判断v是否是在u的子树内
}
该题有两种情况,一种是没有拐点,另一种是有拐点的情况:
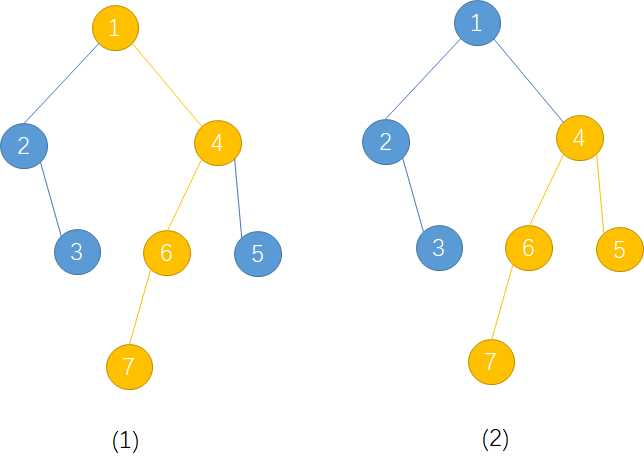
(两种情况)
第一种情况可以直接判断是否在一条链上,将所有的点都放在一个vector上,然后对深度进行排序,这里从小到大排序,然后每次按照相邻的u,v判断是否v是否在u的子树内,如果这一串下来都符合,那么说明这是一条链,如上图(1)。如果不符合,那么就是第二种情况——有拐点的情况。
然后选出两个且在不同边的最深的结点,可以排序也可以sort,找到st和en,也就是上图(2)的st=7,en=5,注意需要是结点两边的,因此不能选en=6。
然后通过st和en找到拐点G=Lca(st,en),也就是上图的4:
vector<int> p(k);
int st = 0, en = 0;
for (int i=0;i<k;i++)
{
cin>>p[i];
if (dep[p[i]]>dep[st]) st = p[i];//先找到最深的结点
}
if (isLink(p)) {cout<<"YES"<<endl;continue;}
for (int i=0;i<k;i++)
{
if (p[i]==st) continue;
if (Lca(st,p[i])!=p[i]&&dep[p[i]]>dep[en])
en = p[i];
}
int G = Lca(st,en);
然后再循环所有的要询问的点,如果满足下列两种情况说明是符合的:
Lca(x,st)==x&&Lca(x,en)==G也就是在st的一边
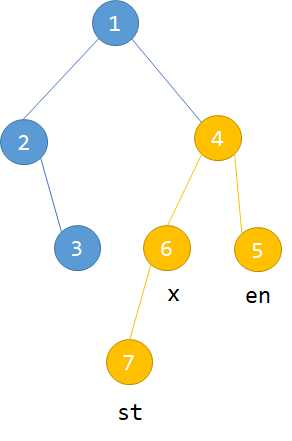
Lca(x,st)==x并且Lca(x,en)==G
Lca(x,st)==G&&Lca(x,en)==x也就是在en的一边
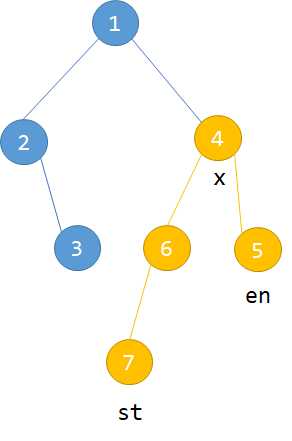
Lca(x,st)==G并且Lca(x,en)==x
for (int x:p)
{
if (Lca(x,st)==x&&Lca(x,en)==G) continue;
if (Lca(x,en)==x&&Lca(x,st)==G) continue;
ok = false;
}
if (ok) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
然后就是LCA的板子了
代码
int head[N],cnte,n,dep[N],f[N][21],lg2[N],q;
struct node
{
int to,next;
}edge[N<<1];
inline void add(int x,int to)
//inline void add(int x,int to,int w)
{
edge[++cnte].to = to;
edge[cnte].next = head[x];
//edge[cnte].w = w;
head[x] = cnte;
}
inline void build(int x,int fa)
{
dep[x] = dep[fa] + 1;
f[x][0] = fa;
for (int i=1;i<=20;i++)
f[x][i] = f[ f[x][i-1] ][i-1];
for (int i=head[x];i;i=edge[i].next)
if (edge[i].to!=fa)
build(edge[i].to,x);
}
int Lca(int x,int y)
{
if (dep[x]<dep[y]) swap(x,y);
while (dep[x]>dep[y])
x = f[x][lg2[dep[x]-dep[y]]];
if (x==y) return x;
for (int i=lg2[dep[x]];i>=0;i--)
if (f[x][i]!=f[y][i])
x = f[x][i], y = f[y][i];
return f[x][0];
}
inline bool cmp(int a,int b)
{
return dep[a]>dep[b];
}
int in[N],out[N],dfn;
inline void dfs(int x,int fa)
{
in[x] = ++dfn;
for (int i=head[x];i;i=edge[i].next)
{
int y = edge[i].to;
if (y!=fa)
dfs(y,x);
}
out[x] = dfn;
}
inline bool isp(int u,int v)
{
return in[u]<=in[v] && out[v]<=out[u];
}
inline bool isLink(vector<int> p)
{
sort(p.begin(),p.end(),cmp);reverse(p.begin(),p.end());
for (int i=1;i<p.size();i++)
if (!isp(p[i-1],p[i])) return 0;
return 1;
}
inline void Case_Test()
{
cin>>n;
for (int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
add(u,v);add(v,u);
}
for (int i=2;i<=N-2;i++)
lg2[i] = lg2[i>>1]+1;
build(1,0);
dfs(1,0);
cin>>q;
while (q--)
{
bool ok = true;
int k;
cin>>k;
vector<int> p(k);
int st = 0, en = 0;
for (int i=0;i<k;i++)
{
cin>>p[i];
if (dep[p[i]]>dep[st]) st = p[i];
}
if (isLink(p)) {cout<<"YES"<<endl;continue;}
for (int i=0;i<k;i++)
{
if (p[i]==st) continue;
if (Lca(st,p[i])!=p[i]&&dep[p[i]]>dep[en])
en = p[i];
}
int G = Lca(st,en);
for (int x:p)
{
if (Lca(x,st)==x&&Lca(x,en)==G) continue;
if (Lca(x,en)==x&&Lca(x,st)==G) continue;
ok = false;
}
if (ok) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
}
signed main()
{
IOS
int _=1;
while (_--)
{
Case_Test();
}
}
