比赛链接:Tasks - UNIQUE VISION Programming Contest 2022(AtCoder Beginner Contest 248)
A - Lacked Number(签到)
这个题有很多种做法,可以sort去找,也可以拿容器(如map)存,我这里想讲我的做法:异或
由于我们知道a ^ b ^ a = b,所以我们一开始可以让ans=0 ^ 1 ^ 2 ^ ... ^ 9,然后对读入进行扫一遍。
inline void Case_Test()
{
cin>>s;
n=s.size();
for (int i=0;i<=9;i++) ans=ans^i;
for (int i=0;i<n;i++) ans=ans^(s[i]-'0');
cout<<ans<<endl;
}
B - Slimes(模拟)
就按照意思去乘,模拟得出答案,这个题没过该打!
C - Dice Sum(DP)
题意:给你一个N位数组,每一位不能超过M,问总和小于K的数有多少种,详细见样例。
这个题有点难度...很不好意思的说我当时没有写出来...
设置一个dp[i][j]表示前i位总和为j的方案数,初始状态是dp[0][0]=1(前0个总和0为1开始转移),然后枚举1...m往新的一位加,我这里用l来枚举1...m。
for (int i=1;i<=n;i++)
for (int j=1;j<=k;j++)
for (int l=1;l<=m;l++)
if (j>=l)
dp[i][j]=(dp[i][j]+dp[i-1][j-l])%mod;
//这里dp[i][j]每次从上一位,总和是j-l转移,这样第i为就是放l(很重要)
因为最后总和不一定达到K,所以还得扫一遍统计答案
for (int i=1;i<=k;i++) ans=(ans+dp[n][i]) % mod;
D - Range Count Query(二分/vector)
题意:给出长度为n的序列,每次询问l,r,x,求区间[l,r]内x出现多少次
这个直接对于每一个a[i]拿vector存位置i,然后对于每一次询问x进行查询,查询就二分查找,找到第一个大于等于l的,和第一个大于r的然后做差法。很简单,至少比C简单
vector<int> v[N];//对于每一个a[i]都开一个动态数组,a[i]保证小于N
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>a[i];
v[a[i]].push_back(i);//存每一位位置
}
int q;
cin>>q;
while (q--)
{
cin>>l>>r>>x;
int t1=lower_bound(v[x].begin(),v[x].end(),l)-v[x].begin();
int t2=upper_bound(v[x].begin(),v[x].end(),r)-v[x].begin();
ans=t2-t1;//这里做差代表中间有多少个
//比如v[5]={1,4,5,8,9,10,13},我询问[4,12]那么t1=1,t2=6,做差法就会得到6-1=5,也就是我想要的{4,5,8,9,10}
cout<<ans<<endl;
}
}
E - K-colinear Line(重要知识点)
题意:给出n个点,求至少经过k的点的直线有多少条
前置知识:我们对于两点间的斜率,我们不用k=dy/dx这样会有精度损失,所以我们用pair来存,比如(1,2)和(3,4)两点,我们能得到dx=3-1=2,dy=4-2=2,然后求出t=gcd(dx,dy)=gcd(2,2)=2,求gcd的目的是为了化简我们拿pair来存分子和分母,这个时候我们存的就是{dy/t,dx/t}={1,1},如果下一次来一个{10,11},{13,14},我们的dx=3,dy=3,t=gcd(3,3)=1,{dy/t,dx/t}={1,1},所以这代表这二者是同一斜率。
那么假如是负数呢?其实也不用管,比如gcd(-10,15)=-5,gcd(10,-15)=5但是当我都除以gcd的时候就变成了{2,-3},{2,-3},这俩还是同一斜率
这个时候我们枚举两个点,然后进行直线统计,如果超过了我们想要的那么就计数,我这里枚举的时候有顺序,只需要统计k*(k-1)/2即可,不难理解的。
那么这个时候问题来了,我现在不仅仅只有斜率,而是一个y=kx+b的直线,这里推荐用一般式Ax+By=C
我们求出dx,dy,t=gcd(dx,dy)然后进行“约分”得到dx=dx/t,dy=dy/t,其实我们的斜率k就已经是k=dy/dx,我们带入一个点,就能得到一般式,注意正负,可以拿草稿纸推算一下得到c=dy*x[i]-dx*y[i],然后我们存直线用map存就好mp[{dx,dy,c}]++,时间复杂度$O(n^2logn)$
map<array<int,3>,int> mp;
inline void Case_Test()
{
cin>>n>>k;
if (k==1) {cout<<"Infinity";return;}//注意特判,经过一个点肯定有无数条
for (int i=1;i<=n;i++) cin>>x[i]>>y[i];
for (int i=1;i<n;i++)
for (int j=i+1;j<=n;j++)
{
int dx=x[i]-x[j],dy=y[i]-y[j];
int t=__gcd(dx,dy);//__gcd函数自带
dx/=t;dy/=t;
c=dy*x[i]-dx*y[i];
//if (xx<0) {xx=-xx;yy=-yy;c=-c;} 这里发现不需要也可
mp[{dx,dy,c}]++;
}
int to=k*(k-1)/2;
for (auto i:mp) if (i.second>=to) ans++;
cout<<ans;
}
F - Keep Connect(连通性状压DP)
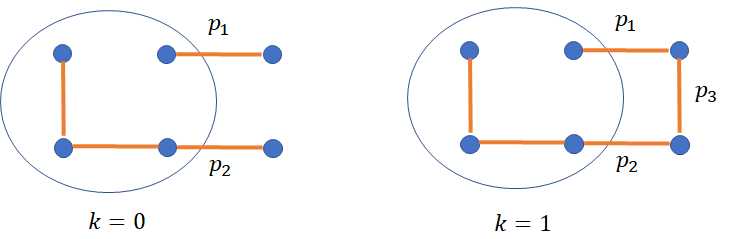
题意:给出n个点3n-2条边成如下图,问每次删1,2,...,n-1条边还满足n点联通的方案数是多少。
我们用dp[i][j][0/1]来表示前i个点已经删除了j条边的连通性,0代表没联通,1代表联通的方案数。
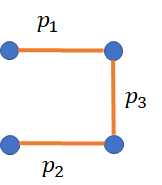
我们枚举$p_1,p_2,p_3$,枚举的方式是0,1,0代表没有,1代表有,分别代表上面几条边,然后对每一次k=0或者k=1进行更新下一次。现在来看两种k的情况:
1)k=0,前面i个是不连通的,但是在后面情况下可能联通
这个情况代表前面是不连通的,如图:
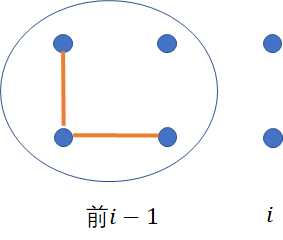
这个时候我们不能要求$p_1,p_2$有一个为0,不然就会导致之后永远不连通,如:
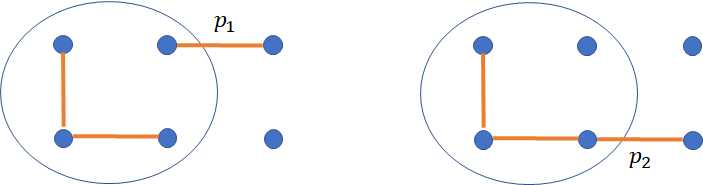
这个时候,接下来转到i+1永远也不会联通了,所以这种情况必须存在$p_1,p_2$。
当然,这个时候就是我们枚举k的两种情况,然后进行更新操作
if (k==0) upd(dp[i+1][j+1-p3][p3],dp[i][j][k]);
2)k=1,前面已经联通,在这一次可以达到不连通或者联通
当然,这个时候如果$p_1,p_2$同时不存在(上一次是有一个不存在就不行),那么肯定就不连通了,因为前i个和第i-1个需要连接,如图是不可以的,肯定不连接。
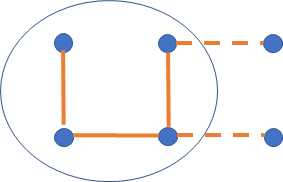
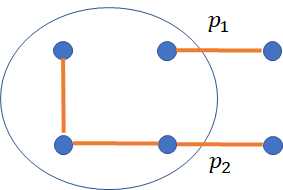
那么在此基础上如果下一次还是连通的话需要满足一个条件,那就是p1+p2+p3>=2也就是至少有两条边(两条或者三条都有),这个时候才是可行的,不然一直下去永远也不会连通,这个时候下一次状态是1,例如:
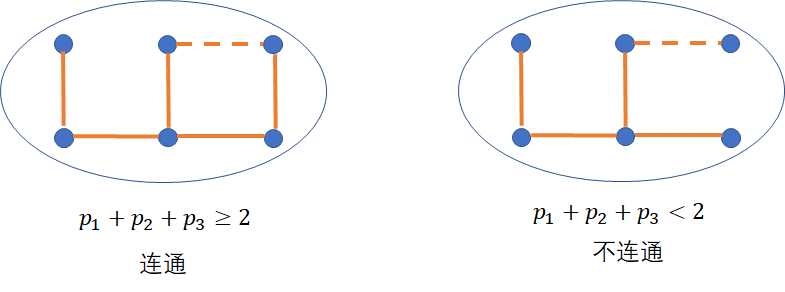
上图右边就是不满足p1+p2+p3>=2的时候,这个时候转移到下一次dp[i+1][k+3-p1-p2-p3][0]的状态,因为这个时候是不连通的。
转移方程:if (k==1) upd(dp[i+1][j+3-p1-p2-p3][(p1+p2+p3)>=2],dp[i][j][k]);
整个代码如下:
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int N = 3e3+7;
int n,p,dp[N][N][2];
void upd(int &a,int b)
{
a+=b;
if (a>=p) a-=p;
}
inline void Case_Test()
{
cin>>n>>p;
dp[1][1][0]=dp[1][0][1]=1;
rep(i,1,n-1) rep(j,0,n) rep(k,0,1)
if (dp[i][j][k])
{
rep(p1,0,1) rep(p2,0,1) rep(p3,0,1)
{
if (k==0&&(p1==0||p2==0)) continue;
if (k==0) upd(dp[i+1][j+1-p3][p3],dp[i][j][k]);
if (k==1&&(p1==0&&p2==0)) continue;
if (k==1) upd(dp[i+1][j+3-p1-p2-p3][(p1+p2+p3)>=2],dp[i][j][k]);
//以上四种情况
}
}
for (int i=1;i<n;i++) cout<<dp[n][i][1]<<" ";
}
