2022牛客多校·第四场

嗯，这回堆积了三场多校总结。这回赛中过四题，补题一题，这场题面越来越差了，越来越讨厌牛客了哈哈。
比赛链接："蔚来杯"2022牛客暑期多校训练营4

小小的总结一下：N是一个思维题，不过也不是很难，死算需要用到分数类+int128；K题是一个思维题；H题是一个思维构造；D是一个二维前缀和；A是一个背包。

两个小时才做出签到...

N.Particle Arts（思维）

题意：给你$n$个粒子，质量为$a_i$，每两个质量为$a,b$粒子之间会发生碰撞生成两个新的（原来的消失）：质量为$a\ OR\ b$和$a\ AND\ b$。求最后趋近于稳态的方差。

思路：我们来看两个数分成按照与和或最后会生成什么，有一个很显然的结论：a + b = (a or b) + (a and b)，也就是说二者的质量不变（符合质量守恒定律哈哈），然后可以看出or是一个很松的，只要有就是；但是and很严格，需要二者都有。

所以把可以把他们看成，每次碰撞会大的越来越大(or)，小的会越来越小(and)，转化成二进制之后相当于一个掉落的过程。所以样例可以看成：

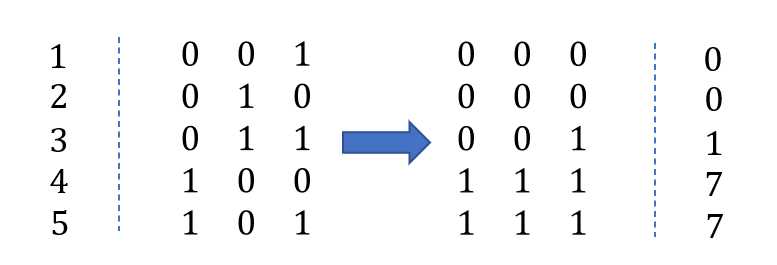
相当于一个掉落的过程

所以样例给出的1 2 3 4 5最后掉落稳态变为0 0 1 7 7，我们只需要求稳态的方差即可。

注意求方差可以用如下公式，避免乘以分母可能导致爆ll

$$
D(x)\ = \ E(x^2) \ - \ E^2(x)
$$

代码：
int128读写

int read(){
    int x=0;bool f=0;char c=getchar();
    while (c<'0'||c>'9'){if (c=='-')f=1;c=getchar();}
    while (c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}

inline void write(int x)
{
     if(x<0) putchar('-'),x=-x;
     if(x>9) write(x/10);
     putchar(x%10+'0');
}

分数类

struct frac{
    int x, y;

    explicit frac(int x = 0, int y = 1):x(x), y(y){
        if (y < 0){
            this -> x = -this -> x;
            this -> y = -this -> y;
        }
    }

    void norm(){
        if (y < 0){
            this -> x = -this -> x;
            this -> y = -this -> y;
        }
        int g = gcd(x, y);
        x /= g;
        y /= g;
    }
    bool operator < (const frac &f)const{
        return x * f.y < y * f.x;
    }

    bool operator > (const frac &f)const{
        return x * f.y > y * f.x;
    }
    friend frac operator + (const frac &a, const frac &b){
        return frac(a.x * b.y + b.x * a.y, a.y * b.y);
    }
    friend frac operator * (const frac &a, const frac &b){
        return frac(a.x * b.x, a.y * b.y);
    }
    friend frac operator / (const frac &a, const frac &b){
        return frac(a.x * b.y, a.y * b.x);
    }
    friend frac operator - (const frac &a, const frac &b){
        return frac(a.x * b.y - b.x * a.y, a.y * b.y);
    }
    friend ostream &operator << (ostream &os, const frac &f){
        write(f.x);putchar('/');write(f.y);
        //os << f.x << "/" << f.y;
        return os;
    }
};

inline void Case_Test()
{
    //cin>>n;
    n = read();
    for (int i=1;i<=n;i++)
    {
        //cin>>x;
        x = read();
        int p = 0;
        while (x)
        {
            cnt[p++]+=(x%2);
            x/=2;
        }
    }//填空
    frac ans;
    int sum = 0;
    for (int i=1;i<=n;i++)
    {
        int res = 0;
        for (int j=0;j<=19;j++)
            if (cnt[j]>=i) res += (1<<j);
        a[i] = res;
        sum += res;
    }
    frac ave = frac(sum,n);
    ave.norm();
    for (int i=1;i<=n;i++)
    {
        frac t = frac(a[i],1) - ave;
        t.norm();
        t = t * t;
        t.norm();
        ans = ans + t;
        ans.norm();
    }
    ans = ans / frac(n,1);
    ans.norm();
    cout<<ans;
}

K.NIO's Sword（思维）

题意：给你一把剑，一开始值为$0$，需要对于按顺序砍掉$1..n$的敌人，对于第$i$个敌人当且仅当$A\ \equiv\ i\ (mod \ n)$才能斩杀，每次可以将剑升级为$A\times 10+x\ (0\leq x\leq 9)$（也就是左移加一位），求斩杀掉$n$个人需要至少多少次升级。

思路：首先想到第i个由上一个i-1构成，也就是上一个已经满足了$A \equiv i-1 \ (mod \ n)$，现在要差$1$，也就是我下方的res = 1，代表差一。那么上一次到现在的距离是多少呢？(i-(i-1)*res%n+n)%n，可以手推一下，如果这个时候大于等于res，说明我需要乘以10来升级，需要加法嘛？不需要，因为这个时候我们什么都可以填，只需要距离小于res即可满足，否则你全填9都不可以。

如果不满足那么就加上升级的次数，并且res*=10，代表升级一次。

代码：

inline void Case_Test()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        int res = 1;
        for (int j=0;j<=6;j++)
        {
            if (( i-(i-1)*res % n +n ) % n < res)
            {
                ans += j;
                break;
            }
            res *= 10;
        }
    }
    cout<<ans;
}

H.Wall Builder II（构造）

题意：给你一个$n$，你有n块1×1的砖头，n-1块2×1的砖头，...,2块(n-1)×1的砖头，1块n×1的砖头。只能横着摆，请问能够成的周长最小的是多少？

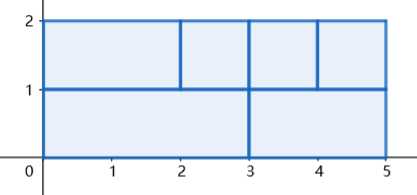
Example

思路：首先来看一共的面积是多少，也就是$n\times 1+(n-1)\times 2+\cdots +2\times (n-1)+1\times n=\frac{(n+2)\times (n+1)\times n}{6}$.

那么现在问题来了，给你一个面积为$s$，求最小周长是多少，从小学学的知识来看，那肯定是正方形的时候最小，但是又因为这是正整数，所以需要判断，这里扫一遍根号即可。

    int area = (n+2)*(n+1)*n/6;
    int t = sqrt(area);
    for (int i=1;i<=n;i++)
        cnt[i] = n-i+1;
    for (int i=t;i>=1;i--)
        if (area%i==0&&area/i>=n)
        {
            a = area/i;
            b = i;
            break;
        }

接下来是如何摆放的问题，因为无法旋转，所以我们只能像上图那样横着摆，我们可以想到——先放大的永远是最好的。例如我当前需要一个3×1的，我是需要用3个1×1的去填吗？不是不行，而是可以放后面放，因为如果这个时候用完了，那么下一次需要1×1的时候就没有用的了。

所以，假如面对一个12×1的，我会从大到小选择，有12×1就放，没有就去看剩下的，设置一个res表示还有多少，一直到其为0为止。

代码：

inline void Case_Test()
{
    cin>>n;
    int area = (n+2)*(n+1)*n/6;
    int t = sqrt(area);
    for (int i=1;i<=n;i++)
        cnt[i] = n-i+1;
    for (int i=t;i>=1;i--)
        if (area%i==0&&area/i>=n)
        {
            a = area/i;
            b = i;
            break;
        }
    int ma = n, res, to;
    cout<<(a+b)*2<<endl;
    for (int i=1;i<=b;i++)
    {
        res = a;
        to = ma;
        cout<<0<<" "<<i-1<<" "<<to<<" "<<i<<endl;
        cnt[to]--;
        res -= to;
        while (cnt[ma]==0) ma--;
        while (res)
        {
            to = Min(res,ma);
            while (cnt[to]==0) to--;
            cout<<a-res<<" "<<i-1<<" "<<a-res+to<<" "<<i<<endl;
            res -= to;
            cnt[to]--;
        }
        while (cnt[ma]==0) ma--;
    }
}

D.Jobs (Easy Version)（二维前缀和）

题意：给你$n(1\leq n\leq 10)$家公司，每家公司有$m(1\leq m\leq 10^5)$个岗位，每个岗位有一个最低限制IQ,EQ,AQ，有$q(1\leq q\leq 2\times 10^6)$次询问，询问一个人的IQ,EQ,AQ能收到多少家公司的offer，只要有一个就算这家公司给offer。

这个题有趣的是强制在线，并且给你一个算法，你必须按照它一个个读入的IQ,EQ,AQ计算出他收到了res家公司的offer，然后这个函数返回之后通过它给你的随机数种子，加上你返回的res计算出新的IQ,EQ,AQ。也就是说它并不是给你的每个人的三个值，而是通过上一次和随机数种子而得出来的。

种子：

#include <random>
std::mt19937 rng(seed);
std::uniform_int_distribution<> u(1,400);

返回:

int lastans=0;
for (int i=1;i<=q;i++)
{
    int IQ=(u(rng)^lastans)%400+1;  // The IQ of the i-th friend
    int EQ=(u(rng)^lastans)%400+1;  // The EQ of the i-th friend
    int AQ=(u(rng)^lastans)%400+1;  // The AQ of the i-th friend
    lastans=solve(IQ,EQ,AQ);  // The answer to the i-th friend
}

思路：
这个题做了很久，一开始以为是三维偏序，实际上前缀和即可。这里用dp[i][j][k][w]表示第w家公司的IQ=i,EQ=j,AQ=w的是否可以，如果这个值是1就代表有。只需要预处理前缀和即可。

这样会爆时间，所以我们选择用bitset来优化，选择用bitset<10> dp[401][401][401];来表示，这样会MLE优化不够，因为我bitset<10>优化不够的，所以需要转化一下变成bitset<401> dp[11][401][401];这样我里面是bitset<401>优化够了。

但是还有一种方法就是，我前缀和保存的不是1,0而是一个最小值，例如我现在的int dp[11][401][401];,定义dp[w][i][j]表示的是第w家公司，IQ=i,EQ=j的AQ最小值。也就是我现在的值保存的是200,150,100这类的数字，这样可以优化一维。

代码：

ll ans[N];
#define tp3 tuple<int,int,int>
vector<tp3> v[11];

int dp[11][401][401];
void work(int w)
{
    for(int i=1;i<=400;i++)
        for(int j=1;j<=400;j++)
            dp[w][i][j] = min ( { dp[w][i-1][j],dp[w][i][j-1],dp[w][i][j]} );//二维前缀和变种，取min
}
inline void init()
{
    for(int vv=1;vv<=n;vv++)
    {
        for(auto e:v[vv])
        {
            int aa,bb,cc;
            tie(aa,bb,cc) = e;//解包
            dp[vv][aa][bb] = Min(dp[vv][aa][bb],cc);
        }
        work(vv);
    }
}
inline int solve(int iq,int eq,int aq)
{
    int res=0;
    for(int i=1;i<=n;i++)
        if(dp[i][iq][eq]<=aq)//如果大于等于最低要求即可
            res++;
    return res;
}

inline int calc()
{
    ll res = 0;
    for (int i=1;i<=q;i++)
        res = (res + ans[i] * qpow(seed,q-i,mod) % mod) % mod;
    return res;
}//需要按照题目的要求计算答案

inline void Case_Test()
{
    n=read();q=read();
    memset(dp,0x3f,sizeof(dp));
    for (int i=1;i<=n;i++)
    {
        m=read();
        for (int j=1;j<=m;j++)
        {
            x = read(); y = read(); w = read();
            v[i].emplace_back(x,y,w);
        }
    }
    init();
    seed = read();
    std::mt19937 rng(seed);
    std::uniform_int_distribution<> u(1,400);
    int lastans=0;
    for (int i=1;i<=q;i++)
    {
        int IQ=(u(rng)^lastans)%400+1;  // The IQ of the i-th friend
        int EQ=(u(rng)^lastans)%400+1;  // The EQ of the i-th friend
        int AQ=(u(rng)^lastans)%400+1;  // The AQ of the i-th friend
        lastans=solve(IQ,EQ,AQ);        // The answer to the i-th friend
        ans[i] = lastans;
    }
    write(calc());
}

A.Task Computing（背包）

题意: 给定 $n(n≤10^5)$ 个物品，每个物品有 $(w_i,p_i)$ 两个值。你需要在这 $n$ 个物品中选择 $m(m \leq 20)$ 个物品，使得这个 $m$ 个物品的权值$\sum_{i=1}^{m} w_{i} * \prod_{j=1}^{i-1} p_{j}$最大

思路：这个式子有些难看，可以换种方法来理解，其权值为 $f$ ，现在我们需要往前面添加一个 $(w_i,p_i)$ 的物品，那么我们的权值会变成 $w_i+p_i\times f$ 。

那么现在有i,j两个物品，我们选择哪个好呢？

• 先选择i，后选择j，代价是$w_j+p_j\times (w_i+p_i\times f)$。
• 先选择j，后选择i，代价是$w_i+p_i\times (w_j+p_j\times f)$。

若先选择i是好的，可以得出：$w_j+p_j\times (w_i+p_i\times f)>w_i+p_i\times (w_j+p_j\times f)$
可以消掉$f$，最后得出$w_{i}\left(1-p_{j}\right)>w_{j}\left(1-p_{i}\right) \Rightarrow \frac{w_{i}}{1-p_{i}}>\frac{w_{j}}{1-p_{j}}$

这样看来发现选择好坏则发现只与自己有关，所以这个时候我们只要比较上述的两个值即可。因为是除法的原因还是选择乘法比较好。

    sort(a+1,a+n+1,[](node &a,node &b){
        return a.w+a.p*b.w<b.w+b.p*a.w;
    });

剩下的就跑背包即可。

代码：

struct node
{
    double p,w;
}a[N];
double f[N][30];
inline void Case_Test()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++)
        cin>>a[i].w;
    for (int i=1;i<=n;i++)
        cin>>a[i].p, a[i].p = a[i].p/10000.0;
    sort(a+1,a+n+1,[](node &a,node &b){
        return a.w+a.p*b.w<b.w+b.p*a.w;
    });
    for (int i=1;i<=n;i++)
        for (int j=1;j<=20;j++)
            f[i][j] = -inf;
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=m;j++)
            f[i][j] = Max(f[i-1][j], a[i].w+a[i].p*f[i-1][j-1]);
    }
    cout<<fixed<<setprecision(10)<<f[n][m]<<endl;
}