
这波还算可以吧,做不出难题,勉勉强强做出三个题,最后又一次压哨绝杀做出03的一个图论,感谢曹佬的指导,不然按照我和队友的方法永远也做不出。还是题目做少了,见识的少了,这个被图论大师一眼秒了。
1010.Bragging Dice(签到)
签到题,按道理来讲先手必胜,但是特殊的地方在如果一个人手上的所有数字都不一样,那么就是0,如果两个都是0那么就输了
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=6;i++) a[i] = b[i] = 0;
bool ok = false;
for (int i=1;i<=n;i++) cin>>x, a[x]++;
for (int i=1;i<=n;i++) cin>>x, b[x]++;
for (int i=1;i<=6;i++)
if (a[i]>1||b[i]>1) ok = true;
if (ok) cout<<"Win!"<<endl;
else cout<<"Just a game of chance."<<endl;
}
1012.Buy Figurines(STL)
题意:给你$n$个人需要排队,有$m$个窗口,每个人给出两个值$\lbrace a_i,s_i\rbrace$,分别表示到达时间以及处理时间。如果当前每个窗口人都满了,则需要选择人数最少的(同人数选择窗口号最小的)。请问最后窗口都没有人的时候是多久以后。
思路:一开始看错题了,我以为都满的时候是选择当前排队时间最少的窗口,仔细一样当你去排队的时候,你也不知道前面人什么时候结束,例如排茶颜悦色的时候前面只有一个人,结果那个人给全班带的,那得等很久...所以这个题目还是挺符合常理的,是我想错了。
首先要知道这里的人是动态的,我们对于到达时间先排序,然后依次处理。例如现在到达的时间是$a_i$,那么$a_i$前结束的人需要全部退出,每次退出还需要更新一下维护的每个窗口的人数。那么如何维护这个呢?
我用一个优先队列来存当前在窗口里面的人的结束时间以及窗口下标id。让结束时间较少的放在堆顶,每次到来$a_i$的人的时候先要保证堆顶要小于$a_i$。
priority_queue<PII,vector<PII>,greater<PII>> q;
那么每个窗口人数怎么维护?每次要选出人数最少的,首先肯定用到优先队列,每次可以取出最小的,但是有一点——取不出中间的,比如我现在1号窗口只有3个人,此时人数最少,但是现在$a_i$进来的时候,需要弹出去一些人,所以这个时候可能4号窗口走出去了2个人,这个时候比1号窗口人少了,这个是优先队列不能完成的。
所以我选择用set,set里面存pair<int,int>分别是人数,以及下标id,为了能通过上面管理窗口人的优先队列得到下标,进而得出set中的值,所以我还需要一个数组来维护当前的人数。然后就模拟就可以了。时间复杂度当然就是$O(nlogn)$的
代码:
struct node
{
int be,s;
}a[N];
int tim[N],num[N];
inline void Case_Test()
{
priority_queue<PII,vector<PII>,greater<PII>> q;//维护窗口的人,{结束时间,窗口下标id}
n = read(); m = read();
for (int i=1;i<=n;i++)
{
a[i].be = read();//到达时间
a[i].s = read();//处理时长
}
set<PII> st;//维护每个窗口的{人数,窗口下标}
for (int i=1;i<=m;i++)
{
st.insert({0,i});//每个窗口0人
num[i] = 0;//每个窗口一开始都是0人
tim[i] = 0;//时间,并不是每个人一来就可以处理的
}
sort(a+1,a+1+n,[](const node& a,const node& b){return a.be<b.be;});//按到达时间排序
for (int i=1;i<=n;i++)
{
while (!q.empty() && q.top().first <= a[i].be)//结束,出窗口
{
int id = q.top().second;q.pop();
st.erase({num[id],id});//删除原来的
num[id]--;//人数减少
st.insert({num[id],id});//重新加入set中
}
int id = st.begin()->second;//取出下标
st.erase({num[id], id});
num[id]++;
st.insert({num[id], id});//a_i进窗口
tim[id] = Max(tim[id], a[i].be) + a[i].s;//每个窗口当前的结束时间
q.push({tim[id], id});//该人的结束时间
}
ans = 0;
for (int i=1;i<=m;i++)
ans = Max(ans, tim[i]);//每个窗口的结束时间
writeln(ans);
}
1003.Slipper(图论,虚点)
题意:给你$n$个点的一棵树,每条边有权值,特殊的是还给出两个值$k$和$p$,表示对于任意两个点$u,v$,如果$|dep_u-dep_v|=k$,那么这两点$u,v$就建立一条权值为$p$的边。最后给出起点和终点,求二者的最短路。(为了计算深度,根为$1$)
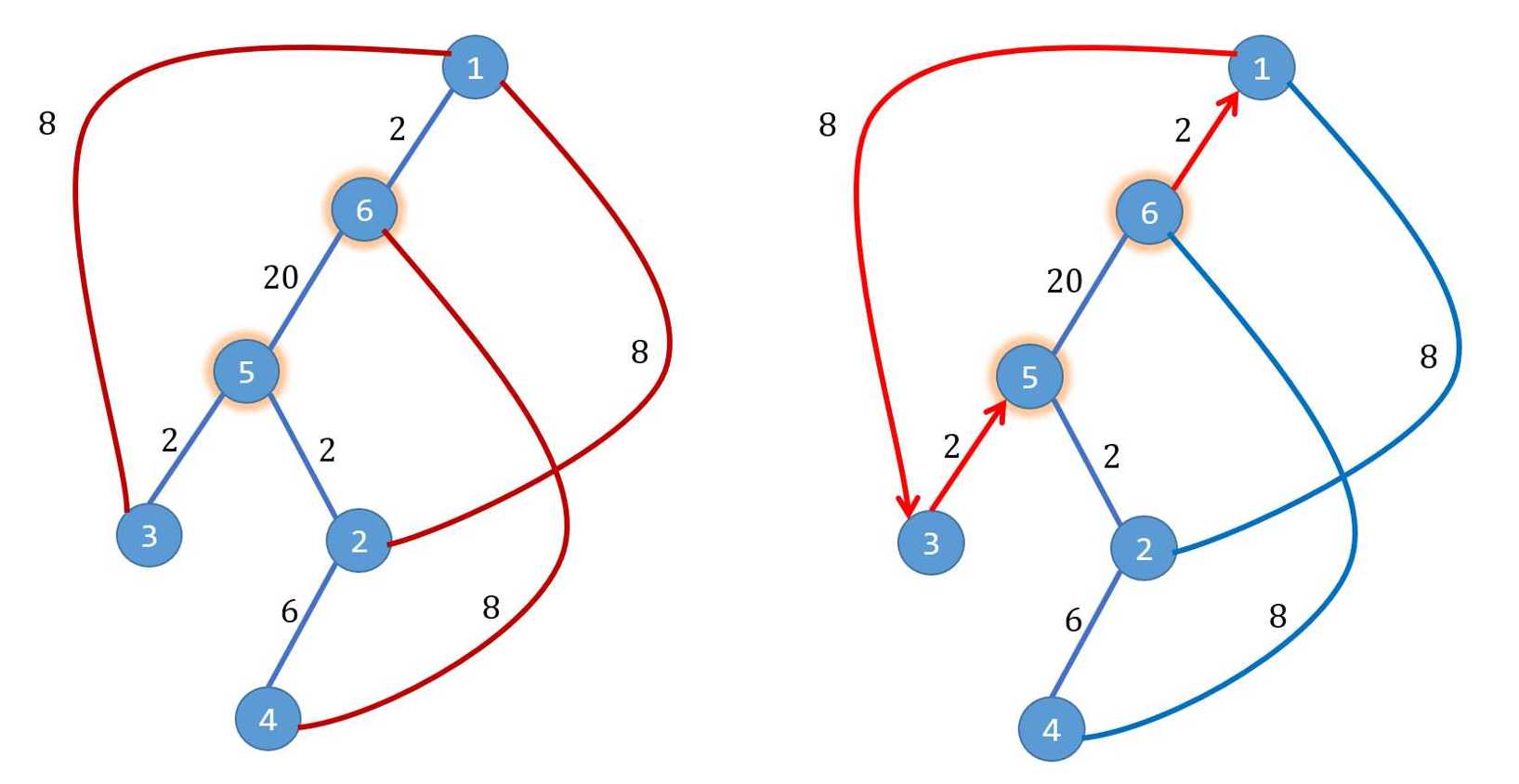
k=3,p=8,起点是6终点是5。选择6->1->3->5,距离是2+8+2=12
思路:虚点操作。对于每一层进行设置多设置一个点,我这里叫层点,例如深度为$1$的点就命名为$n+1$,这样上面使用魔法可以跳跃$k$层转化成树上的点到层点,然后由层点到树上的点的操作。
具体如何操作的呢?例如上图的1号可以花费p=8到达k=3之后的3号点。所以我先让1连接dep[1]+k号层点,距离是p,然后由层点到达3号点则需要花费0(注意一定是单向边,不然同层的点可以互相0花费跳跃)。
怎么理解呢?举个例子,现在要实现1号点往3和2号点实现跳跃,我先将1号点连接层点。
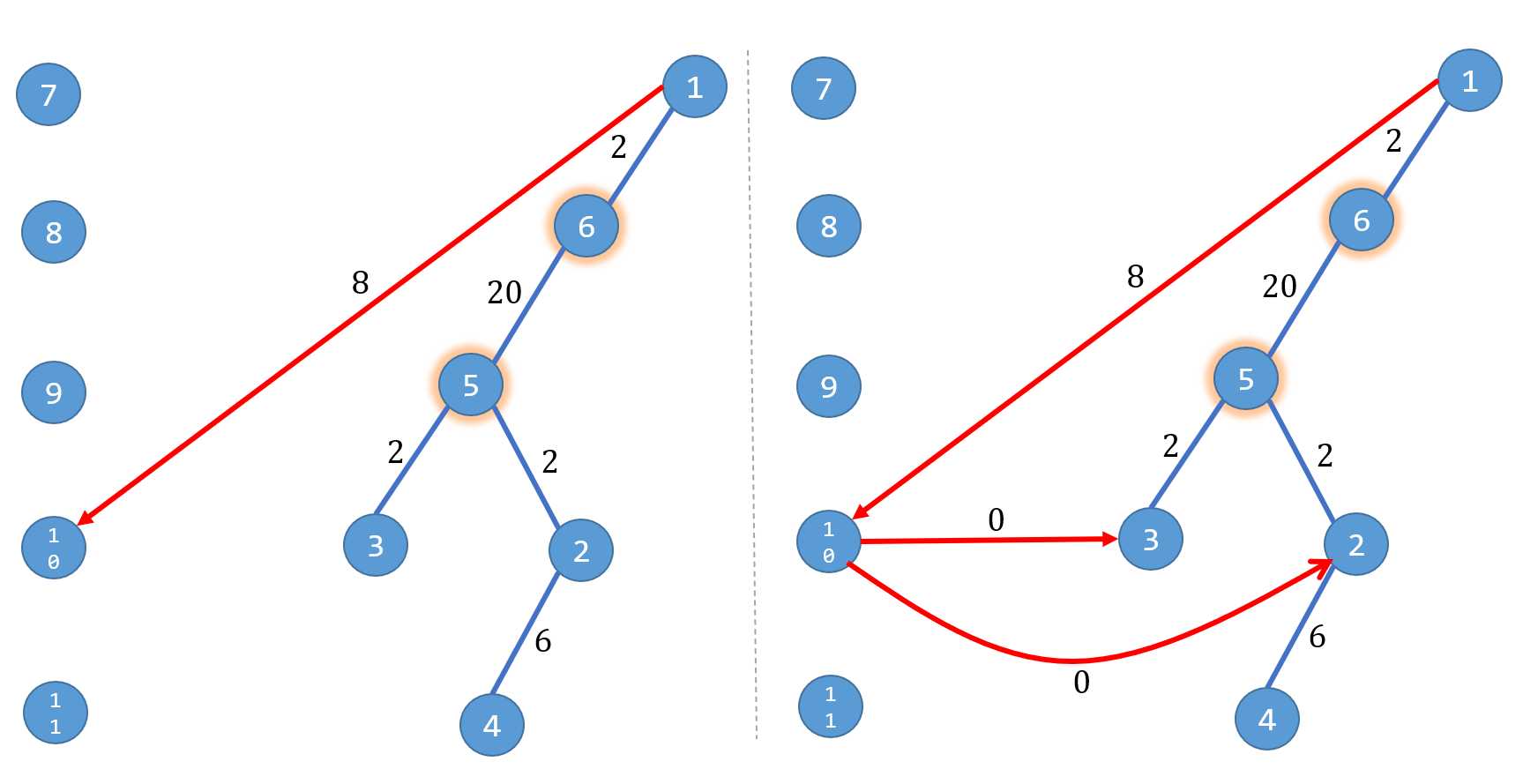
实现1号点跳跃操作
这样能节省大量时间空间,就按照这个操作跑最短路即可。
所以最后整张图跑出的是
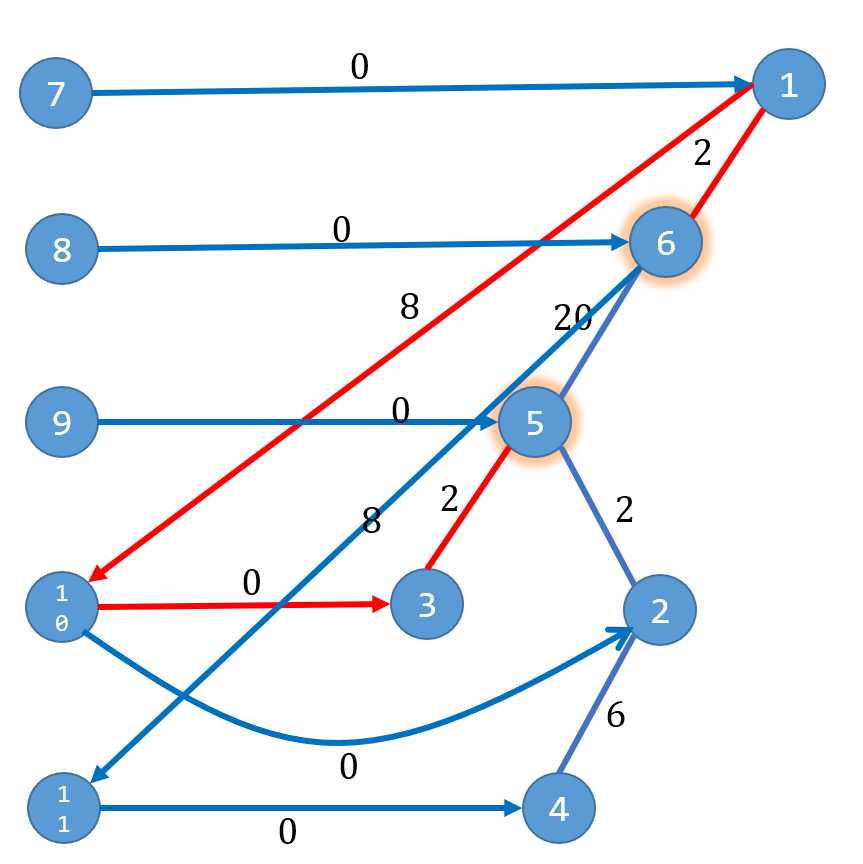
最后的最短路(因为太乱的缘故,2,3,4往上跳跃的未画出)
代码:
vector<int> Dp[N];
inline void Dij(int s, int t)
{
memset(dis, 0x7f / 2, sizeof(dis));
memset(vis, 0, sizeof(vis));
dis[s] = 0;
priority_queue<pair<int, int>> Q;
Q.push({0, s});
while (!Q.empty())
{
int x = Q.top().second;
Q.pop();
if (vis[x])
continue;
vis[x] = true;
if (x == t)
break;
for (int i = head[x]; i; i = edge[i].next)
{
int y = edge[i].to, w = edge[i].w;
if (dis[y] > dis[x] + w)
{
dis[y] = dis[x] + w;
Q.push({-dis[y], y});
}
}
}
cout << dis[t] << endl;
}
inline void dfs(int x, int pre)
{
dep[x] = dep[pre] + 1;
maxDep = Max(maxDep, dep[x]);
Dp[dep[x]].push_back(x);
for (int i = head[x]; i; i = edge[i].next)
if (edge[i].to != pre)
dfs(edge[i].to, x);
}
inline void Case_Test()
{
cin >> n;
dfn = 0;
maxDep = 0;
memset(head, 0, sizeof(head));
cnt = 0;
for (int i = 1; i < n; i++)
{
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
add(v, u, w);
}
cin >> k >> p;
cin >> st >> en;
dfs(1, 0);
for (int i = 1; i <= maxDep; i++)
{
for (int j : Dp[i])
{
add(n + i, j, 0);
}
}
for (int i = 1; i <= n; i++)
{
if (dep[i] + k <= maxDep)
{
// debug2(i,dep[i]+n+k);
add(i, dep[i] + n + k, p);
//add(dep[i] + n + k, i, p);
}
if (dep[i] - k >= 1)
{
add(i, dep[i] + n - k, p);
//add(dep[i] + n - k, i, p);
}
}
Dij(st, en);
for (int i = 1; i <= maxDep; i++)
Dp[i].clear();
}
