牛客小白月赛F（根号trick）

今天写牛客小白月赛的时候，做完前三题看到第四题是一个模拟，就没有写了，直接去看做的人数较多的F，做法直接让我大开眼界...
题目链接：牛客小白月赛F-困难卷积

题意：

给出两个序列$a_i,b_i$，求出：

$$
\sum_{i=1}^{n} \sum_{j=1}^{n}\left \lfloor \sqrt{\left|a_{i}-b_{j}\right|} \right \rfloor
$$

范围是：
$1\le n\le 10^6, 0\le a_i,b_i \le 3\times 10^6, \Sigma a_i,\ \Sigma b_i\le 10^7$

思路

这里一开始注意到特殊的地方，也就是为什么给出$a,b$序列的总和小于等于$10^7$，重点就是在这里：

根号trick：序列$a_i$中不同数字的个数小于等于$\sqrt{\Sigma a_i}$

其实这么一想，已知总和$sum$，问最多有多少个不同的$a_i$来构成。我们可以用贪心的方法，例如上面的总和是$10^7$，所以我们从最小的开始选，选$1,2,3,\cdots$，假如最大选到$m$，那么可以得出目前的总和是

$$
sum^\prime = 1+2+3+\cdots +m-1+m=\frac{(1+m)\times m}{2}\le sum=10^7
$$

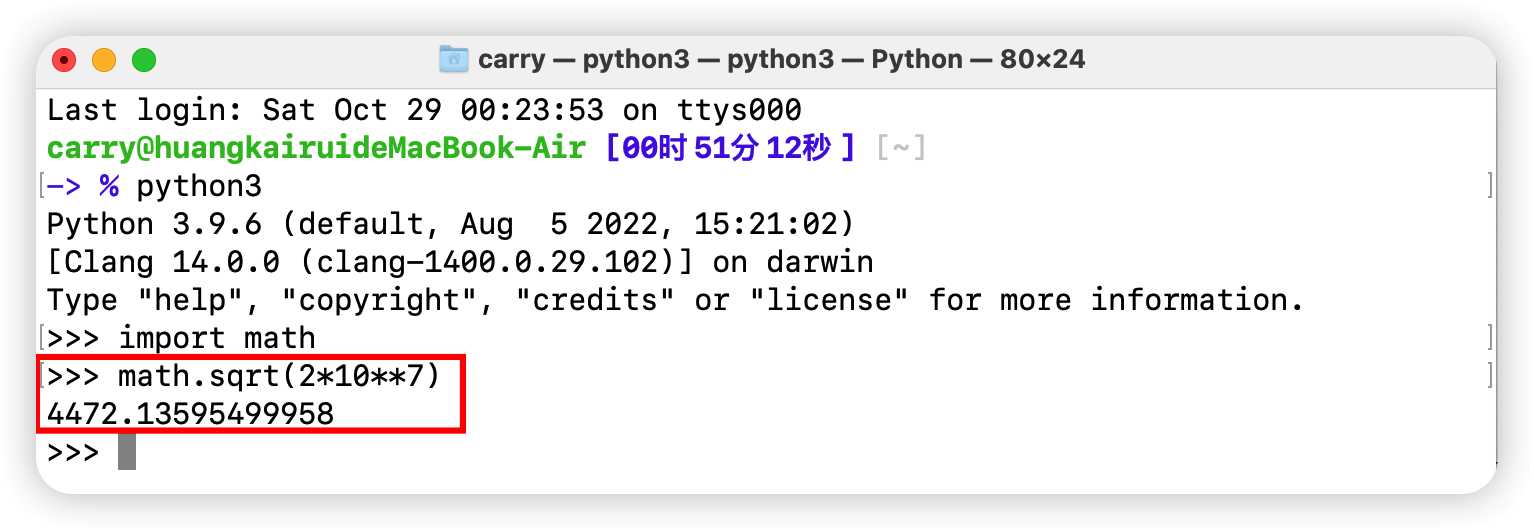
所以能够得出来$m$最多是$\sqrt{2\times 10^7}=4472$，姑且算它$5000$吧，所以这样平方级别的复杂度完全可以通过。

那么这个$m=5000$能够说明什么呢？之前的$n=10^6$，这样差别很大，说明一定一定一定有很多重复的数字，所以我们完全不用重复枚举，一个数字重复出现我们只算一次，具体请看代码就懂啦～

代码

map<int,int> mpa, mpb;
inline void Case_Test()
{
    cin>>n;
    for (int i=1;i<=n;i++) cin>>x, mpa[x]++;
    for (int i=1;i<=n;i++) cin>>x, mpb[x]++;
    for (auto &[x, na]:mpa)
        for (auto &[y, nb]:mpb)
            ans += (int)sqrt(Abs(x-y))*na*nb;
    cout<<ans;
}

补充

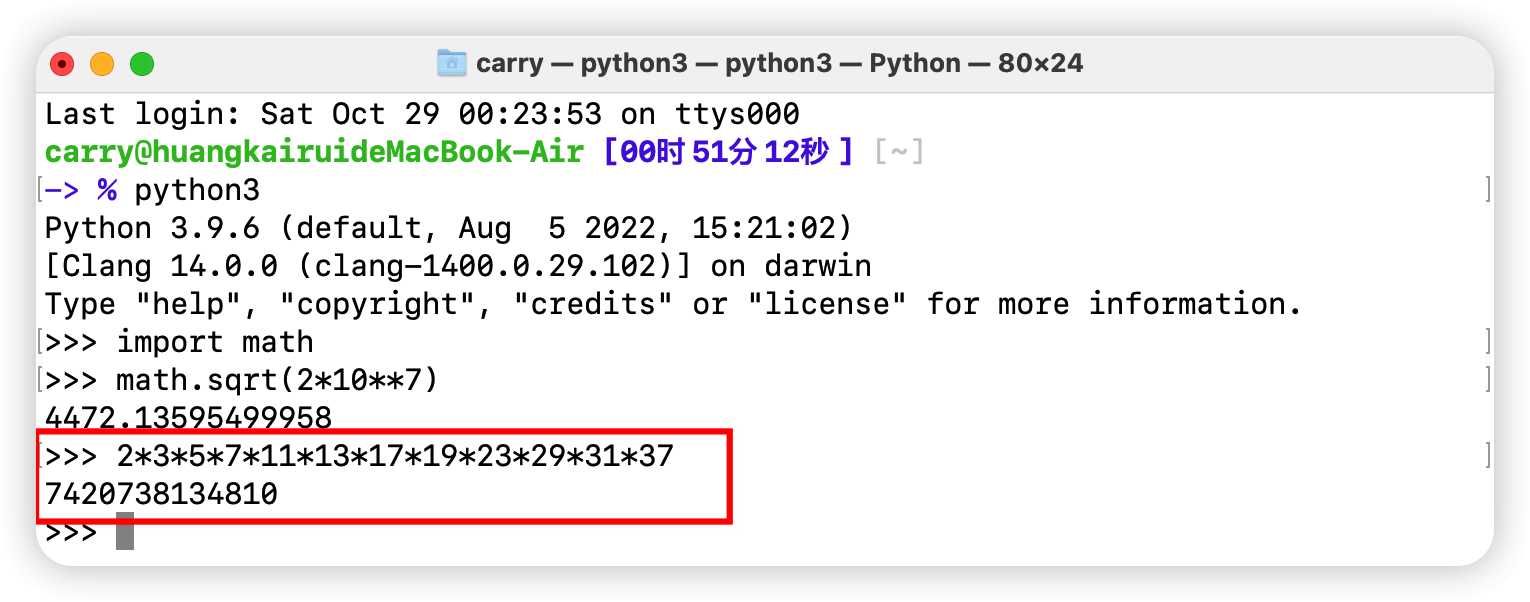
与此类似的，还有给你一个很大的数字，实际上能够拆分的不同的质因数也只有少数刚过$10$个，一般差不多是$12$个。