CF1712D.Empty Graph 贪心｜multiset｜平衡树 2000

题意

题目链接Codeforces Round #813 (Div. 2) - D. Empty Graph

给你一个长度为$n$的序列，以及一个整数k，这是一个无向完全图，两点(l,r)之间的路径长度为

$$
dis(l,r)\ =\ min\lbrace a[l],a[l+1],\cdots,a[r-1],a[r]\rbrace
$$

你可以将一个点的权值求改为小于等于1e9的任意值，可以修改最多k个点。

求图的直径的最大值。

图的直径：任意两点(u,v)之间最短距离的最大值

思路

先来看任意两个点(i,j)之间的距离：

有两种情况：

• 一种是直接从i到j，花费min{a[i],a[i+1],...,a[j]}
• 一种是从i到k花费a[k]，从k到j花费a[k]，也就是花费2*a[k].（其中a[k]是外面最小值）

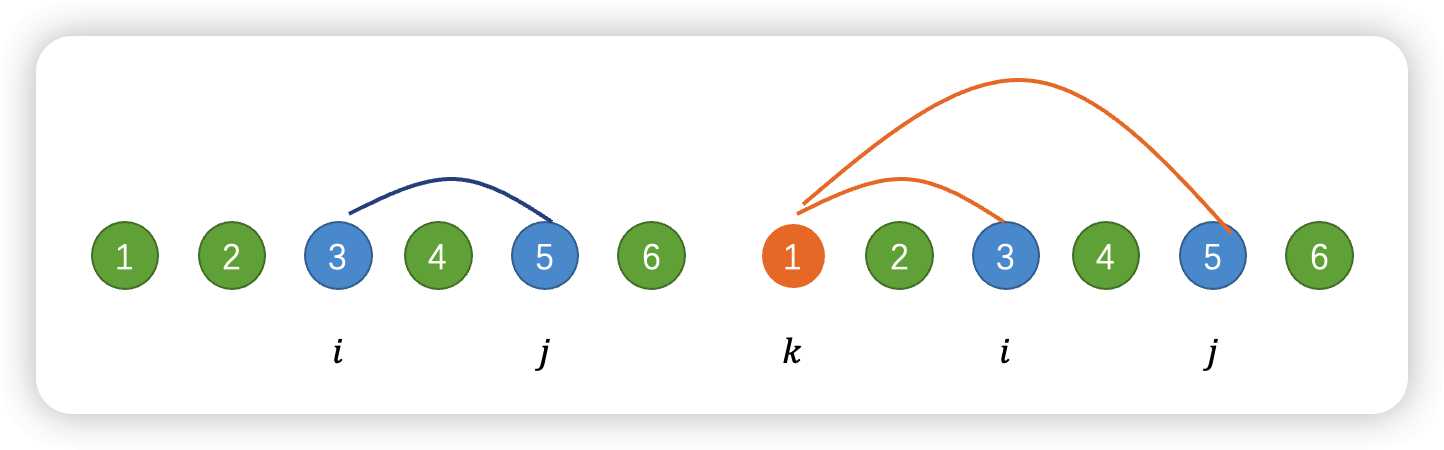
两种情况

所以我们有

$$
dis(i,j) = min\lbrace 2\times a[1],2\times a[2],\cdots a[i],a[i+1],\cdots ,a[j],\cdots ,2\times a[n]\rbrace
$$

也就是外面的点乘以2，内部的点乘以1的最小值就是距离。

重点来了：我想要$dis(i,j)_{max}$，那么就想要里面一长串的值越小越好，这样才有可能把最小值提升，也就是有如下关系：

$$
dis(i,j)\leq dis(i,i+1)
$$

为什么可以这么看，因为在$dis(i,j)$中，我可以要$a[i+1]$后面的$a[i+2],\cdots ,a[j-1],a[j-2]$变成$2\times a[i+2],\cdots ,2\times a[j-1],2\times a[j-2]$。这样就有可能把我选择的最小值提升（如果原来需要选择的在$(i+1,j]$内。

所以我只需要枚举$(i,i+1)$，把$\lbrace 2\times a[1],\cdots ,a[i],a[i+1],\cdots ,2\times a[n]\rbrace$这些数字进行排序，可以用$k$次操作将最小的$k$个数字变成$10^9$，这样也就是选择第$k+1$个小的数是当前的答案。

所以枚举$n-1$次得到的答案的最大值，就是我修改$k$次之后的答案，图的直径的最大值。

那么如何进行“排序”并且求出第$k+1$个小的数字呢？

可以发现从当前的$(i,i+1)$变成$(i+1,i+2)$的时候，只有几个数字发生改变：

• 插入$2\times a[i-1]$
• 插入$a[i+1]$
• 删除$a[i-1]$
• 删除$2\times a[i+1]$

本文重点来了，可以用平衡树来做，不过这个题学到了一种方法就是用multiset：

我用两个multiset<int> s1,s2，s1一直保持k个数字，然后其他数字都放到了s2中。

• 插入x。
  先比较s1个数是否比k小，说明还没有填满，那么就放入s1.insert(x)中。
  如果已经有k个了，那么就把s1中最大的数字拿出来比较，如果x要大，那么说明不是这些数k小的数字，那么就放到s2中。否则把s1中最小的删除放到s2中，再加入x。

inline void MSinsert(int x)
{
    if (s1.size()<k) s1.insert(x);
    else
    {
        auto it = s1.end();
        it--;
        if (x>*it) s2.insert(x);
        else s2.insert(*it), s1.erase(it), s1.insert(x);
    }
}

• 删除x
  先看看是不是比s1的最大值要小，如果是那么说明在s1中删除，并且要从s2中补充一个过来，因为要一直保持s1是k个。否则就在s2中删除。

inline void MSerase(int x)
{
    auto it = s2.begin();
    if (x>=*it) s2.erase(s2.find(x));
    else
    {
        s1.insert(*s2.begin());
        s2.erase(s2.begin());
        s1.erase(s1.find(x));
    }
}

注意
在multiset中删除一个值是把这里面若干个值都删除，删除迭代器则是删除迭代器指向的位置。

• 查询
  既然s1是k个小的，那么s2中最小的就是我需要的，修改后的最小值。

inline int MSKth()
{
    return *s2.begin();
}

先预处理填好，然后枚举一遍即可。

代码

multiset<int> s1,s2;
inline void MSinsert(int x)
{
    if (s1.size()<k) s1.insert(x);
    else
    {
        auto it = s1.end();
        it--;
        if (x>*it) s2.insert(x);
        else s2.insert(*it), s1.erase(it), s1.insert(x);
    }
}
inline void MSerase(int x)
{
    auto it = s2.begin();
    if (x>=*it) s2.erase(s2.find(x));
    else
    {
        s1.insert(*s2.begin());
        s2.erase(s2.begin());
        s1.erase(s1.find(x));
    }
}
inline int MSKth()
{
    return *s2.begin();
}
inline void MSinit()
{
    s1.clear();s2.clear();
    MSinsert(a[1]);MSinsert(a[2]);
    for (int i=3;i<=n;i++)
        MSinsert(2*a[i]);
    ans = MSKth();
}
inline void Case_Test()
{
    cin>>n>>k;
    for (int i=1;i<=n;i++) cin>>a[i];
    if (k==n) {cout<<inf<<endl;return;}
    MSinit();
    for (int i=2;i<n;i++)
    {
        MSinsert(2*a[i-1]);
        MSinsert(a[i+1]);
        MSerase(a[i-1]);
        MSerase(2*a[i+1]);
        ans = Max(ans, MSKth());
    }
    cout<<Min(ans,inf)<<endl;
}

PS：学了平衡树我再来做这个题。