题意
给你一个$N$个点,形成如下的图,求删除$i=\lbrace 1...N-1 \rbrace $条边,$N$个点依然联通的方案数,对$P$取模,数据范围:$2\leq N \leq 3000$
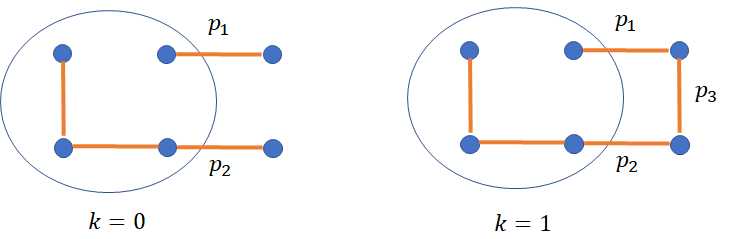
这样的图是有$N$个点,$3N-2$条边,例如样例$N=3$的时候,当分别删除$1,2$条边的时候的方案数如下:

思路
我们用dp[i][j][0/1]来表示前i个点已经删除了j条边的连通性,0代表没联通,1代表联通的方案数。
注意我这里说的没联通代表前面i个虽然是不连通的,但是在今后的情况下是有可能连通的,比如不存在一开始两个就跟后面所有断了联系的
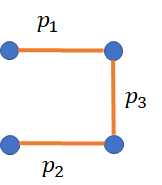
我们枚举$p_1,p_2,p_3$,枚举的方式是0,1,0代表没有,1代表有,分别代表上面几条边,然后对每一次k=0或者k=1进行更新下一次。现在来看两种k的情况:
1)k=0,前面i个是不连通的,但是在后面情况下可能联通
这个情况代表前面是不连通的,如图:
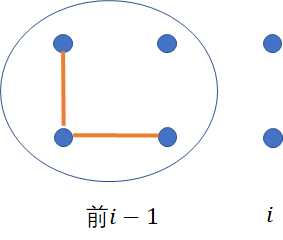
这个时候我们不能要求$p_1,p_2$有一个为0,不然就会导致之后永远不连通,如:
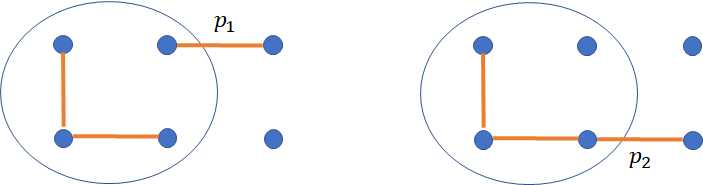
这个时候,接下来转到i+1永远也不会联通了,所以这种情况必须存在$p_1,p_2$。
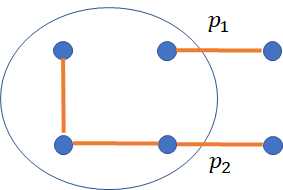
当然,这个时候就是我们枚举k的两种情况,然后进行更新操作
if (k==0) upd(dp[i+1][j+1-p3][p3],dp[i][j][k]);
2)k=1,前面已经联通,在这一次可以达到不连通或者联通
当然,这个时候如果$p_1,p_2$同时不存在(上一次是有一个不存在就不行),那么肯定就不连通了,因为前i个和第i-1个需要连接,如图是不可以的,肯定不连接。
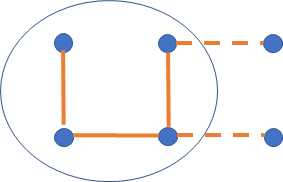
那么在此基础上如果下一次还是连通的话需要满足一个条件,那就是p1+p2+p3>=2也就是至少有两条边(两条或者三条都有),这个时候才是可行的,不然一直下去永远也不会连通,这个时候下一次状态是1,例如:
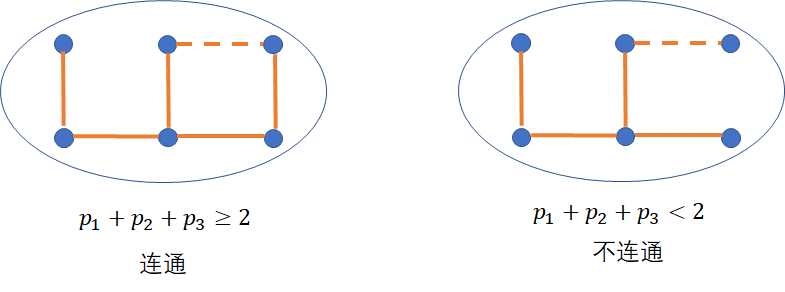
上图右边就是不满足p1+p2+p3>=2的时候,这个时候转移到下一次dp[i+1][k+3-p1-p2-p3][0]的状态,因为这个时候是不连通的。
转移方程:if (k==1) upd(dp[i+1][j+3-p1-p2-p3][(p1+p2+p3)>=2],dp[i][j][k]);
代码
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int N = 3e3+7;
int n,p,dp[N][N][2];
void upd(int &a,int b)
{
a+=b;
if (a>=p) a-=p;
}
inline void Case_Test()
{
cin>>n>>p;
dp[1][1][0]=dp[1][0][1]=1;
rep(i,1,n-1) rep(j,0,n) rep(k,0,1)
if (dp[i][j][k])
{
rep(p1,0,1) rep(p2,0,1) rep(p3,0,1)
{
if (k==0&&(p1==0||p2==0)) continue;
if (k==0) upd(dp[i+1][j+1-p3][p3],dp[i][j][k]);
if (k==1&&(p1==0&&p2==0)) continue;
if (k==1) upd(dp[i+1][j+3-p1-p2-p3][(p1+p2+p3)>=2],dp[i][j][k]);
//以上四种情况
}
}
for (int i=1;i<n;i++) cout<<dp[n][i][1]<<" ";
}
感谢dls视频教的此题,让我第一次对ABC的F有了突破!
