越来越菜了,想当年我第一把abc是在去年的暑假,那时候就是一千名...F是个DP,稍后补一下。
比赛链接:Tasks - freee Programming Contest 2022(AtCoder Beginner Contest 264)
A - "atcoder".substr() (签到)
题意:
给你字符串atcoder以及两个数L,R,求第[L,R]的字符串
思路:for循环输出即可,记得先-1或者在前面加上一个空格
代码:
inline void Case_Test()
{
s = " atcoder";
cin>>n>>m;
for (int i=n;i<=m;i++) cout<<s[i];
}
--
B - Nice Grid(切比雪夫距离)
题意:给出一个$15\times 15$的下图图,并且给出x,y,求第x行第y个的颜色。

黑白相间的,n=m=15
思路:我打算先生成这个图,但是如何生成呢?我是先打算生成$15\times 15$的黑的,然后再-1生成$14\times 14$的白的,然后-1生成$13\times 13$的黑的...
才发现,其实这个就是切比雪夫距离...
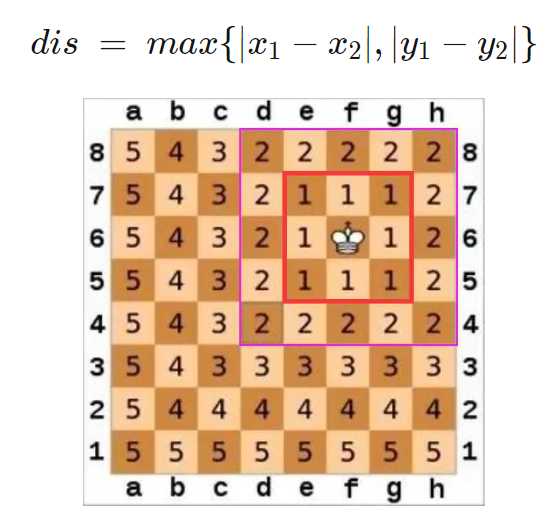
切比雪夫距离
请见文章:欧式距离、曼哈顿距离、切比雪夫距离 - CarryNotKarry
代码:
inline void col(int x,int y)
{
for (int i=x;i<=y;i++)
for (int j=x;j<=y;j++)
c[i][j] = ch;
}
inline void Case_Test()
{
n = 15;
for (int i=1;i<=8;i++)
{
if (i%2==1) ch = 'B';//先染黑
else ch = 'W';
col(i,n-i+1);
}
cin>>x>>y;
if (c[x][y]=='B') cout<<"black";
else cout<<"white";
}
一行切比雪夫距离代码:
cin >> n >> m;
cout << (max(abs(n - 8), abs(m - 8)) % 2 ? "black" : "white") << endl;
C - Matrix Reducing(状压枚举)
题意:给你两个矩阵$A,B$,问是否能通过对矩阵$A$删除若干行和若干列(可以为$0$)而得到矩阵$B$
思路:状压枚举,不过我不太熟练,就debug了好久。比如有h1行,那么就for (int i=0;i<(1<<h1);i++)这个状态就是i,第j为若为1则表示删除第j行,然后列也是如此。暴力匹配看看对不对即可。
数1有多少个可以用__builtin_popcount(x)函数。
代码:
inline void Case_Test()
{
cin>>h1>>w1;
for (int i=1;i<=h1;i++)
for (int j=1;j<=w1;j++)
cin>>a[i][j];
cin>>h2>>w2;
for (int i=1;i<=h2;i++)
for (int j=1;j<=w2;j++)
cin>>b[i][j];
auto calc = [&](int x)
{
int res = 0;
while (x)
{
if (x&1) res++;
x/=2;
}
return res;
};
for (int i=0;i<(1<<h1);i++)
{
int r1 = h1 - calc(i);
if (r1!=h2) continue;
for (int j=0;j<(1<<w1);j++)
{
int r2 = w1 - calc(j);
if (r2!=w2) continue;
r1 = i, r2 = j;
int c1 = 0, c2 = 0;
bool ok = true;
for (int k=0;k<h1;k++)
{
if ((r1>>k)&1) continue;
x = k+1;
c1++;c2 = 0;
for (int l=0;l<w1;l++)
{
if ((r2>>l)&1) continue;
y = l+1;
c2++;
if (a[x][y]!=b[c1][c2]) ok = false;
}
}
if (ok) {Yes;return;}
}
}
No;
}
D - "redocta".swap(i,i+1)(暴力)
题意:给你一个atcoder字符串的一个排列,求经过如下操作0次或者若干次得到atcoder的最小操作是多少。
- 选择两个相邻的字母交换
思路:
我直接模拟,用了s.insert(),s.erase()的函数,对于应该为atcoder的顺序枚举,对于当前字符c看在哪里,然后距离就是我们需要花费的。
代码:
string st = " atcoder";
map<char,int> pos;
inline void Case_Test()
{
cin>>s;
n = 7;
s = " "+s;
for (int i=1;i<=n;i++)
pos[st[i]] = i;
for (int i=1;i<=n;i++)
{
c = st[i];
for (int j=1;j<=n;j++)
{
if (s[j]==c)
{
ans += Abs(j-i);
s.erase(j,1);
s.insert(pos[c],1,c);
break;
}
}
}
cout<<ans;
}
E - Blackout 2(染色/并查集)
题意:给你n个城市以及m个发电站,以及e条边组成一张图。然后有q次询问,每次询问首先给出一个值x,表示e条边中的第x条失效。
请问每次失效之后有多少城市还可以是有电的。
思路:这个题差不多算一个原题把,是2021Robocom的7-4 疫情防控:(12条消息) 2021 RoboCom 世界机器人开发者大赛-本科组(初赛)题解_CarryNotKarry的博客-CSDN博客。也是给出来一个图,然后慢慢拆边,每次询问。
对于这样的题目应该怎么想?应该倒着想,一开始边是最少的,然后慢慢加。 可以用并查集但是我这题不太会用...其实也是可以的,后面放脱老师的代码以及思路。
然后每次加边,如果当前有是被染色(也就是能够发电的),那么就给另外一个还没有被染色的进行dfs,dfs就是遍历他的边,如果它连接的也有没被染色的话,那么就需要被染色。这样会超时嘛?不会,每个点最多一次。
for (int i=q;i>=1;i--)
{
int id = query[i];
ans[i] = cnt;
x = v[id].fi;
y = v[id].se;
add(x,y);add(y,x);;
if (col[x]||col[y])
{
if (!col[x]) dfs(x);
if (!col[y]) dfs(y);
}
}
但是我就是这个地方tle了两发,下面是我tle的代码
if (col[x]) cnt--,dfs(x);
if (col[y]) cnt--,dfs(y);
我是想的对于可以染色的,就对于它的边扫一遍,但是后面发现如果是菊花图,也就是这个点连了很多边,他就不应该被开始进入那么多次,所以这里tle了。
大致的思路就是,先存所有的输入,对于没有被删的边进行建图并且染色,然后每次加一条边就按照上面的对两边的点进行判断。
脱老师有个观点讲得好:
把所有发电站看成一个点,每次查询发电站所在的集合大小就行了
就是如果城市的数量等于集合的大小就说明里面全是城市所以就是没有通电的
代码:
struct node
{
int to,next;
}edge[N<<1];
inline void add(int x,int to)
{
edge[++cnte].to = to;
edge[cnte].next = head[x];
head[x] = cnte;
}
inline void dfs(int x)
{
col[x] = 1;
cnt++;
bool ok = true;
for (int i=head[x];i;i=edge[i].next)
{
int y = edge[i].to;
if (col[y]) continue;
dfs(y);
}
}
inline void Case_Test()
{
cin>>n>>m>>e;
vector<PII> v(e+1);
for (int i=1;i<=e;i++)
cin>>v[i].fi>>v[i].se;
for (int i=n+1;i<=n+m;i++)
col[i] = 1;
cin>>q;
for (int i=1;i<=q;i++)
{
cin>>query[i];
vis[query[i]] = 1;
}
for (int i=1;i<=e;i++)
{
if (vis[i]) continue;
x = v[i].fi;
y = v[i].se;
add(x,y);add(y,x);
col[x] |= col[y];
col[y] |= col[x];//一开始的染色
}
for (int i=1;i<=n+m;i++)
if (col[i]) dfs(i);
cnt = 0;
for (int i=1;i<=n;i++)
if (col[i]) cnt++;
for (int i=q;i>=1;i--)
{
int id = query[i];
ans[i] = cnt;
x = v[id].fi;
y = v[id].se;
add(x,y);add(y,x);;
if (col[x]||col[y])
{
if (!col[x]) dfs(x);
if (!col[y]) dfs(y);
}
}
for (int i=1;i<=q;i++)
cout<<ans[i]<<endl;
}
下面是脱老师的代码:
struct UF {
vector<int> fa, sz, city;
int count = 0;
UF(int n, int m) : fa(n), sz(n, 1), city(n) {
iota(fa.begin(), fa.end(), 0);
fill(begin(city), begin(city) + m, 1);
}
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
bool same(int x, int y) { return find(x) == find(y); }
bool join(int x, int y) {
x = find(x), y = find(y);
if (x == y) return false;
if (sz[x] > sz[y]) swap(x, y);
if (city[x] == sz[x] && city[y] < sz[y]) count += city[x];
if (city[y] == sz[y] && city[x] < sz[x]) count += city[y];
fa[x] = y;
sz[y] += sz[x];
city[y] += city[x];
return true;
}
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m, e;
cin >> n >> m >> e;
vector<array<int, 2>> edges(e);
for (auto& [u, v] : edges) {
cin >> u >> v;
u--, v--;
}
int q;
cin >> q;
vector<int> query(q), is_broken(e), ans(q);
for (auto& x : query) {
cin >> x;
x--;
is_broken[x] = 1;
}
UF uf(n + m, n);
for (int i = 0; i < e; i++) {
if (!is_broken[i]) {
de(edges[i]);
uf.join(edges[i][0], edges[i][1]);
}
}
ans[q - 1] = uf.count;
for (int i = q - 1; i > 0; i--) {
uf.join(edges[query[i]][0], edges[query[i]][1]);
ans[i - 1] = uf.count;
}
for (int i = 0; i < q; i++) {
cout << ans[i] << '\n';
}
}

