一、题目
给定10名成年男子运动员的100米、1500米、跳远、铅球、标枪成绩,设计算法对其运动水平进行高水平--低水平分类。
| 100米 | 1500米 | 跳远 | 铅球 | 标枪 | |
|---|---|---|---|---|---|
| 甲 | 10.92 | 03:42.2 | 5.24 | 16.37 | 76.94 |
| 乙 | 11.45 | 03:58.3 | 5.68 | 12.58 | 57.21 |
| 丙 | 10.35 | 03:49.9 | 6.3 | 13.51 | 47.39 |
| 丁 | 12.91 | 04:28.4 | 6.67 | 15.21 | 76.19 |
| 戊 | 13.03 | 04:36.5 | 4.99 | 18.95 | 57.54 |
| 己 | 11.67 | 04:08.1 | 7.03 | 12.44 | 44.44 |
| 庚 | 11.21 | 03:56.8 | 6.66 | 12.21 | 56.35 |
| 辛 | 12.90 | 04:12.7 | 5.84 | 14.86 | 63.80 |
| 壬 | 11.31 | 03:51.1 | 5.53 | 13.61 | 63.80 |
| 癸 | 10.53 | 03:55.5 | 6.02 | 12.80 | 50.49 |
二、问题重述
给定十个人的五项运动成绩数值,设计算法为其运动水平进行分类为“高水平“和”低水平“。
三、解决方法
本题用到了k-means聚类的方法,基于欧式距离的聚类算法,认为两个目标的距离越近,相似度越大,然后可以将其分为若干类,在这里是分为两类,分别为代表“高水平”和“低水平”。
3.1 初始化
将数据导入,这里将数据原封不动的存入data中,并且也设置name存放名字。
data = {
'甲': [10.92, 222.2, 5.24, 16.37, 76.94],
'乙': [11.45, 238.3, 5.68, 12.58, 57.21],
'丙': [10.35, 229.9, 6.30, 13.51, 47.39],
'丁': [12.91, 268.4, 6.67, 15.21, 76.19],
'戊': [13.03, 276.5, 4.99, 18.95, 57.54],
'己': [11.67, 248.1, 7.03, 12.44, 44.44],
'庚': [11.21, 236.8, 6.66, 12.21, 56.35],
'辛': [12.90, 252.7, 5.84, 14.86, 63.80],
'壬': [11.31, 231.1, 5.53, 13.61, 63.80],
'癸': [10.53, 235.5, 6.02, 12.80, 50.49]
}
name = ['甲', '乙', '丙', '丁', '戊', '己', '庚', '辛', '壬', '癸']
因为100米和1500米成绩数值是越低越好,跳远、铅球和标枪是越高越好,所以为了统一,可以选择对后三项乘以-1来变为负数,这样的话五项属性都是越低越好。
cluster = 2 #分为两簇
dimension = 5 #五项成绩,维度为5
total_cluster = len(data) #总共有多少个人
for i in data:
data[i][2] = data[i][2] * (-1.0)
data[i][3] = data[i][3] * (-1.0)
data[i][4] = data[i][4] * (-1.0)
#取反处理
3.2 函数介绍
这里一开始需要选择两个点作为质心,用getClusterId()函数即可随机出两个数,如果相同的话则继续随机,直到不相同为止。
def getClusterId(name):
x,y = random.randint(0, 9), random.randint(0, 9)#随机两个数,代表找两个人作为质心
while x==y:#如果相同,那么继续随机,直到不相同为止
x,y = random.randint(0, 9), random.randint(0, 9)
return name[x], name[y]
算法需要计算欧氏距离,也就是上述所言,距离越近代表相似度越大,就越可能归为一类,欧氏距离:$dis\left(x,y\right)=\sqrt{\sum_{i=1}^{n}\left(x_i-y_i\right)^2}$
def getDistance(data, cur, tar):
res = 0.0
for i in range(len(cur)):#枚举所有的成绩
res += (data[cur][i] - tar[i])**2#计算两个人的距离
return res**0.5#欧几里得距离
3.3 K-means聚类算法
一开始需要随机选出两个点作为质心,来计算所有的数据到质心的距离进而进行下一步处理。
x,y = getClusterId(name)
cluster_center1,cluster_center2 = data[x],data[y]
#print(cluster_center1,'\n',cluster_center2,sep='')
然后设置距离的列表,用于存放所有数据分别到所有质心的距离。
dis = [[0.0]*cluster for v in range(total_cluster)]
这里需要引入两个列表,$cluster_type\left[i\right]$和$pre_cluster_type\left[i\right]$分别代表i的当前类型和前一个类型。之所以这么做是可以用于优化,当类型不变的时候,通过我们的算法可以得出质心是不会发生变化的,因为质心也就是当前簇的平均值。
cluster_type = [ [0.0] for v in range(total_cluster) ]
pre_cluster_type = cluster_type.copy()
然后我们设置最大迭代次数max_iter=1000(后面通过运行发现,实际上短短几次就可以结束迭代)。
max_iter = 1000
然后正式开始迭代:
- 1) 计算距离。
遍历所有的数据,对所有质心求距离,会得到一个$10\ast2$的二维数组$dis\left[i\right]\left[j\right]$代表第i个人到与第j个的距离。
for i in range(len(data)):
x = getDistance(data,name[i],cluster_center1)
y = getDistance(data,name[i],cluster_center2)
#print(x,y)
dis[i] = [x,y]
- 2) 将数据归类。
对于每一个人,比较其到二者的距离,取最小的放入1类;最大的则放入2类,并且统计个数,以便最后取平均值。
numType1 = 0
numType2 = 0 #统计个数
#print(cluster_center1)
#print(cluster_center2)
for i in range(len(data)):
if dis[i][0] < dis[i][1]:#距离较小的
cluster_type[i] = 1#归为1类
numType1 += 1#1类数量+1
else:
cluster_type[i] = 2#归为2类
numType2 += 1#2类数量+1
print('u=',u)
print('pre:',pre_cluster_type)
print('cur:',cluster_type)
- 3) 判断是否迭代结束。
if cluster_type == pre_cluster_type:#如果两次的类型一样,那么结束循环
break
pre_cluster_type = cluster_type.copy()#否则pre继承这一次的结果,以便下一次判断
- 4) 求和取平均,得到新的质心。
如果迭代还在继续,则取每一簇的平均值作为新的质心,作用于下一次迭代。
sigma1 = [ 0.0 for v in range(dimension) ]
sigma2 = [ 0.0 for v in range(dimension) ]
for i in range(len(data)):
for j in range(dimension):
if cluster_type[i] == 1:
sigma1[j] += data[name[i]][j]#加入至对应类型的和
else:
sigma2[j] += data[name[i]][j]#加入至对应类型的和
#print('sigma1:',sigma1,'\nsigma2:',sigma2,sep='')
for i in range(dimension):
sigma1[i] /= numType1
sigma2[i] /= numType2#对每一簇除以总个数即为平均数
#sigma1和sigma2即为新的质心
cluster_center1 = sigma1.copy()
cluster_center2 = sigma2.copy()
四、运行结果
运行结果可以看出,这次运行随机到了四次,第四次的时候两类不变,推出迭代。
结果是$\left[2,2,2,1,1,2,2,1,2,2\right]$,也就是{甲,乙,丙,己,庚,壬,癸}和{丁,戊,辛}两类。
因为这是有一定的随机算法,所以进行多次实验。
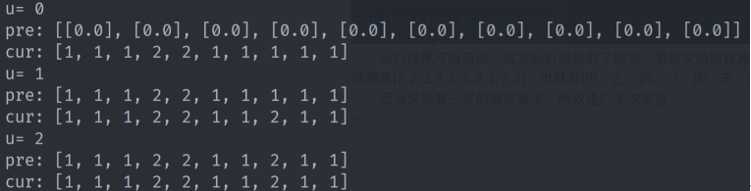
第二次实验可以看出,迭代到了第二次发现类跟上一次不变,推出迭代,结果是$\left[1,1,1,2,2,1,1,2,1,1\right]$,与上一次答案虽然不一样,但是分出来的类也是一样的,同样是{甲,乙,丙,己,庚,壬,癸}和{丁,戊,辛}两类。
再进行10次运行可以发现,迭代次数到$u=\lbrace 1,2,3,1,5,1,2,1,1\rbrace$截至,经过多次实验,发现一般不超过5次即可迭代结束,原因是数据量太少,只有10个人;也发现有很多一次两次,原因也是因为分成的两类分别为7个和3个,这样也有数据量太少和分布有些许不均匀有关系,所以也很有可能选择质心就是我们所需要的,一次即可。
五、总结与分析
我们通过结果以及规律(常识),可以选出两类中的{甲,乙,丙,己,庚,壬,癸}为“高水平”运动员,而{丁,戊,辛}为“低水平”运动员。