题目
2022年天梯赛决赛的前一晚,来几道二叉树的题目(RP++)
给你一个完美二叉树的前N项的后序遍历,求它的层序遍历
我的思考
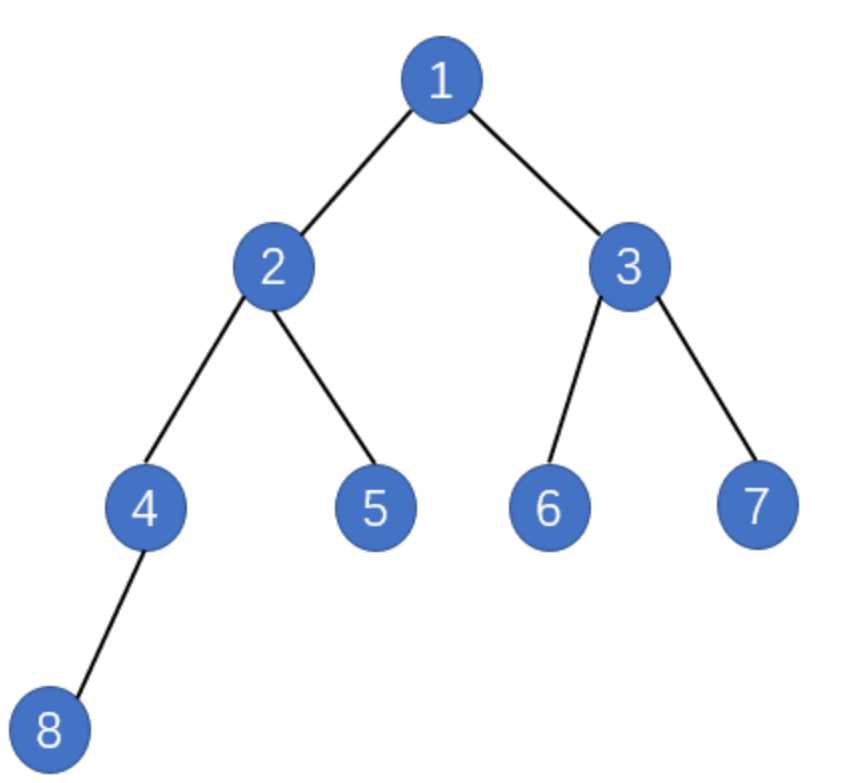
我的思路是根据每个点往下有多少个子结点,因为给我的最后一个肯定是根,然后递归往下找。
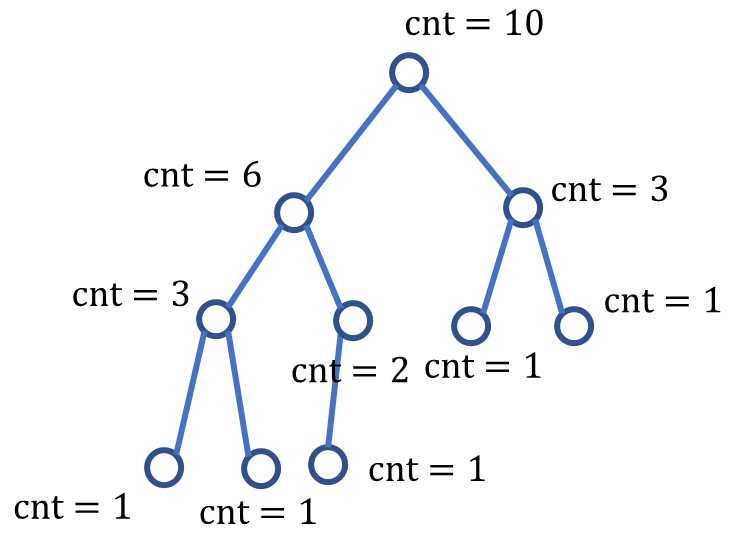
我用一个我自己的样例,就是上图的10个
10
91 83 71 14 2 34 10 15 55 18
这个18肯定是根,前一个肯定是它的右结点,但是每一个数的前一个不一定是右结点,因为有可能不存在,所以我们判断一下:
inline void dfs(int x,int p)
{
if (p<=0||x>n) return;
tree[x].v=a[p];
if (tree[2*x+1].cnt) dfs(x*2+1,p-1);//如果右边还需要有数目,那就传
dfs(x*2,p-1-tree[x*2+1].cnt);//不然传左边
}
统计的这个cnt就比较好统计,直接往下传就好,大于n的话就return,最后像线段树那样在加起来即可
因为是二叉树,只需要for循环输出就好
for (int i=1;i<=n;i++) cout<<tree[i].v<<" ";
总代码:
struct node
{
int l,r,cnt=0,v;
node(){}
}tree[110];
inline void count(int x)
{
tree[x].cnt=1;
if (x*2<=n) count(x*2);
if (x*2+1<=n) count(x*2+1);
tree[x].cnt+=tree[x*2].cnt+tree[x*2+1].cnt;
}
inline void dfs(int x,int p)
{
if (p<=0||x>n) return;
tree[x].v=a[p];
if (tree[2*x+1].cnt) dfs(x*2+1,p-1);
dfs(x*2,p-1-tree[x*2+1].cnt);
}
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>a[i];
to[i]=a[i];
}
int p=n;
count(1);
dfs(1,p);
for (int i=1;i<=n;i++) cout<<tree[i].v<<" ";
}
最简单正解
void build(int x){
if(x>n) {
return ;
}
build(2*x);//左
build(2*x+1);//右
//根,后续遍历
cin>>level[x];//递归完毕再读入
}
int main() {
cin>>n;
build(1);
rep(i,1,n){
cout<<level[i];
if(i<n) cout<<" ";
}
return 0;
}
