在之前3DGS部分讲了很多,但今天重新看了一下这个公式,因为最近论文总是能看到这些,比如深度图。我们先来看渲染每个像素的颜色是怎么渲染的。
首先就是对于每一个像素出发,它会经过很多的高斯,每个高斯肯定会做出一定的贡献,那么这个贡献怎么来的呢?每个高斯都有一个值叫不透明度,这个也类似一个权重,这个值越大那么就会越阻碍后面的高斯,并且也要符合光学的原理,光线也是有能量的,前面阻挡完了后面当然就看不见了。那么直觉上来看,比起这条线很少的高斯,一条线很多的高斯它并不是无限叠加的。
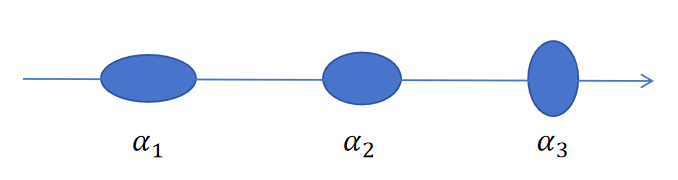
所以,应该这么思考。每条光都是有限的能量,比如就是1.0。在经过第一个高斯的时候,它的不透明度假如是\alpha_1 = 0.5,那么经过它之后还剩下多少呢?还剩下0.5,这个值当然是由1.0-\alpha_1而来的,那么假如下一个高斯的\alpha_2=0.3,又会是什么样的呢?那么就是剩下的0.5经过这个\alpha_2=0.3的高斯,那么相当于经过这个高斯需要损失0.3(30\%).我们就观察这个高斯:
- 它的贡献:经过前的
0.5然后真正有贡献的是那个0.3,所以它的贡献就是0.5\times 0.3\cdot f,这的f可以是颜色也可以是深度 - 它的损失:到来前的
0.5“花费”了0.3,那么还有0.7可以继续往下走,那么也就是0.5\times 0.7可以继续走下去
那么到这个高斯,前面损失过后还剩下多少呢?实际上就是我们论文里面的T_i,即
T_i=\prod_{j=1}^{i-1}(1-\alpha_i)再乘上我们现在这个高斯的贡献\alpha_i=(1-\exp(-\sigma_i\delta_i)),就是这个高斯对这条射线的贡献T_i\alpha_i。其实这里说“贡献”有点不太对,因为还没有说是什么的贡献,是颜色?还是深度?实际是正如我上面的f一样,再乘以它即可,比如我要求颜色,那么每个高斯能够给这个像素增加的贡献就是T_i\alpha_ic_i,那么所有的高斯呢?就是我们论文里面的公式
C=\sum_{i=1}^NT_i\alpha_ic_i最后也可以写成论文公式(3)的样子,如下图

我们举一个例子,假如现在有3个高斯,它们分别的参数是不透明度\alpha_1=0.5,\alpha_2=0.3,\alpha_3=0.8,他们距离相机的深度分别是d_1=2,d_2=5,d_3=8,我们现在计算深度图的时候需要得到这个像素的深度值。首先我们计算经过每一个高斯的时候,还会剩下多少,那么很容易得到
T_1=1.0\quad T_2=1\times (1-\alpha_1)=0.5 \quad T_3=0.5\times (1-0.3)=0.35然后通过这个可以计算出w_i=T_i\times \alpha_i,实际上就是计算这个高斯能够提供多少的“贡献”(还没有算属性的),可以得到
\begin{aligned}
w_1&=T_1\cdot \alpha_1=1.0\times 0.5=0.5\\
w_2&=T_2\cdot \alpha_2=0.5\times 0.3=0.15\\
w_3&=T_3\cdot \alpha_3=0.35\times 0.8=0.28
\end{aligned}那么这个像素就是再乘以属性即可,结果是D=\sum w_id_i=0.5\times 2+0.15\times 5+0.8\times 8=3.99,那么这个像素的深度值就是3.99\approx 4
那么在对于提取表面的时候,经常可以看到他们选取的是中值,比如取0.5的位置就是表面,我们定义累积分布函数“
F(t)=\sum_{d_i\leq t}w_i它表示“射线到深度t之前被拦住的概率”,当F(t)=0.5的时候表示有一半的光在t之前被吸收了,直觉上这个就是表面。
比如上面这个样例,就可以得到F(d_1)=0.5,F(d_2)=0.6,F(d_3)=0.93,那么在位置d_1的地方就是我们的表面。
-
写在最后,这个公式给人的感觉就是,有一束光,经过阻碍物(高斯),有多少被阻拦(做贡献),另外的那多少就漏过去。
-
而表面提取的时候经常取期望或者
0.5的,说实话我还没太明白为什么选0.5但整体而言这个值最佳,而不是0.3或者0.7,这个经验和稳定性优先 -
对于法线图的时候
N并不太一样,而是
N=\dfrac{\sum_i w_i\cdot n_i}{\Vert \sum_i w_i\cdot n_i\Vert} 每一个高斯都有一个法线向量n_i,然后加权做归一化。其实法线图也可以看作是“对法线的期望”,最后再归一化。
- 这个体渲染公式有一个很好的,它控制
\sum w_i在[0,1]之间,保证了如果经过了所有的还少,那么就是背景颜色了,可以通过数学公式证明的,因为保证了\sum w_i=1-T_{N+1}\leq 1
