Surface Reconstruction from Point Clouds without Normals by Parametrizing the Gauss Formula

团队主页链接：https://jsnln.github.io/tog2022_pgr/
TOG2022，在Siggraph2023进行展示

概括：这篇文章提出了一种基于参数化高斯公式的方法，用于从没有法向量的点云中进行重建。不依赖数据驱动，而是基于高斯公式在势理论（Potential Theory）中的应用。高斯公式描述了一个区域的指示函数如何通过边界积分表示。因此，将表面法向量和表面元素面积视为位置参数，利用高斯公式来求解这些参数，同时获得指示函数。
项目代码：https://github.com/jsnln/ParametricGaussRecon
关键词：
表面重建，高斯公式，3D形状建模，基于点的模型，网格模型

1. Introduction

表面重建解决了将点云转化为网格的问题。

本文的贡献：

提出参数化高斯重建（PGR）方法，基于高斯方程。
引入线性化表面元（LSEs）。
采用共轭梯度法。

核心优势：

无须预先计算点云法向量，可以处理无定向输入数据
通过高斯公式建立参数化模型
适用于噪声、稀疏点云、非均匀分布的挑战数据集

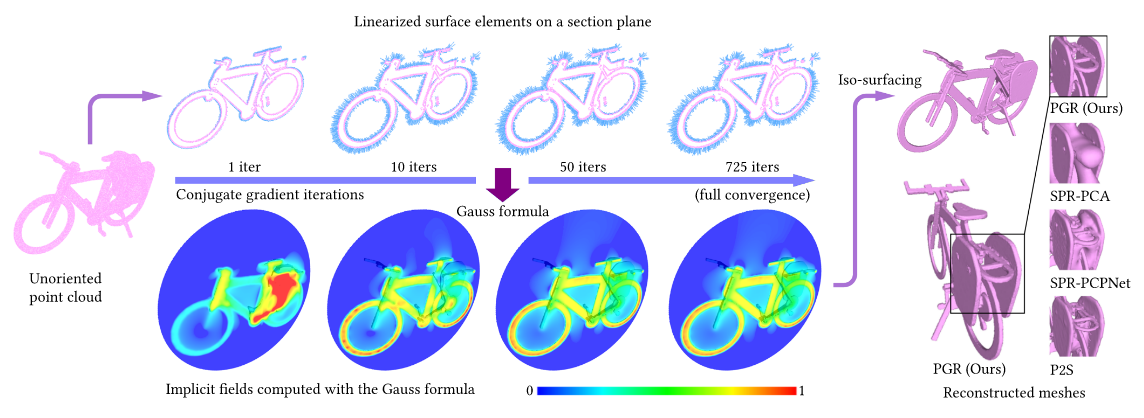
至此，我提出来了一些疑问，到时候看完整篇文章再进行提问

📌这篇文章输入和输出是什么？

输入是一个无向点云，输出是一个带有法向量的三角网格（Mesh），并且具有一致的法向量方向

📌这个隐式场是什么？感觉和SDF（有符号距离函数）很像

有点像，但不完全相同

隐式场 (Implicit Field) 是一种连续的函数，可以用来定义一个表面（网格）。
在重建过程中，它用于判断某个空间点是否在物体表面、内部还是外部。

PGR这里计算的是使用高斯公式计算，类似于指示函数，值接近于1就在表面上，接近于0就在表面外。与SDF不同的点在于SDF计算的有符号距离，正负表示内外，而PGR方法的隐式场在于高斯公式计算出来的指示函数

📌线性化表面元（LSEs）是什么？

（存）

📌高斯公式和指示函数分别是什么？

（存）

2. Related Work

不过多阐述，有：

组合方法
隐式方法
1. 需要输入法向量的参数化方法
2. 需要输入法向量的非参数化方法
3. 不需要输入法向量的方法
  1. 基于PCA的法向量估计
  2. 变分方法：引入额外的平滑能量来正则化隐式场。
  3. 无符号距离场
  4. 深度学习
相关性分析：与现有方法的关系

PGR（参数化高斯重建）与径向基函数（RBF）方法在某些方面是相似的
1. PGR方法同样使用了附加到输入点的基函数，并且也面临类似的问题，如非均匀采样和计算效率
2. PGR和Hermite RBF方法都包含向量值的基函数
PGR（参数化高斯重建）与传统的RBF方法相似，但有两点关键不同：
- PGR基函数并非基于插值或光滑性假设，而是受高斯公式启发。
- PGR能够生成一致的法向量方向，确保表面重建的正确性。

📌思考：RBF（径向基函数，Radial Basis Function）是什么

我理解的RBF本质上就是一耳光关于距离的映射函数，值仅仅依赖于与中心点的欧几里得距离，即
\phi(r)=\phi(\Vert x-x_i\Vert)
并且与选择的核有关（核和单调性有关），例如：

高斯核\phi(r)=e^{-\beta r^2}：单调递减

多二元核\phi (r)=\sqrt{r^2+\beta^2}：单调递减

逆多二次核\phi(r)=\dfrac{1}{\sqrt{r^2+\beta^2}}：单调递减

代码：RBF三种核的可视化代码

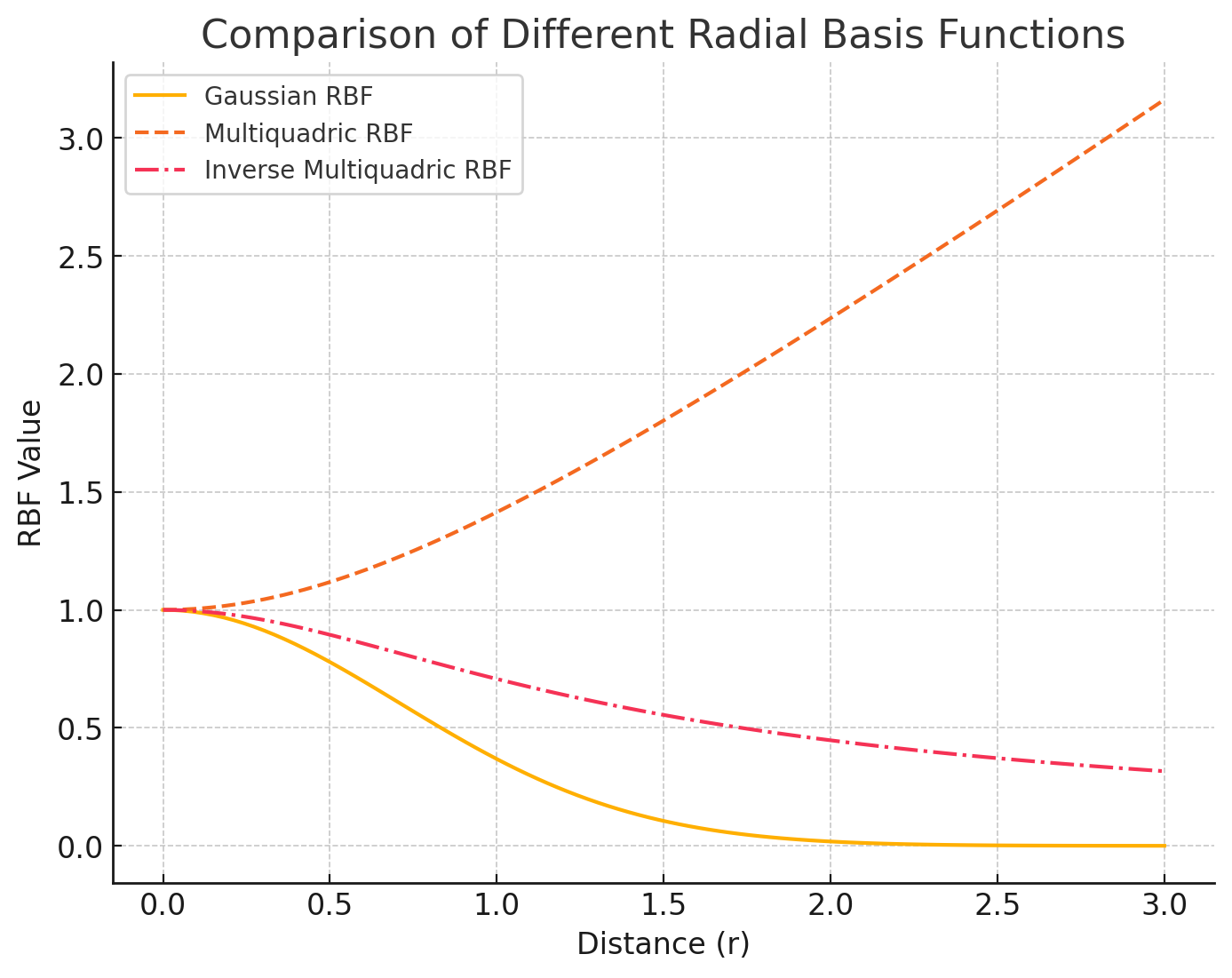
我们希望使用RBF将离散的点云拟合成连续的表面，给定一组点云X能够得到一个隐式函数f(x)使得在点云上f(x_i)=0,而内部为负，外部为正

假设f(x)由一组RBF线性函数组成：
f(x)=\sum_{i=1}^{N}w_i\phi(\Vert x-x_i\Vert)+P(x)
w_i是系数，P(x)是一个低阶多项式，用于补偿全局趋势

拟合过程：

求解权重w_i，使得函数f(x)在已知点云上逼近，即f(x_i)=0

现在得到了w_i，那么就可以计算任意位置的x

提取等值面：Marching Cubes算法https://zhuanlan.zhihu.com/p/639901209

3. PARAMETRIC GAUSS RECONSTRUCTION（PGR）

这里会详细介绍方法和参数高斯重建。首先介绍高斯公式，最后介绍最终指示函数

3.1 Preliminary预备知识

假设\Omega是\mathbb{R}^3的一个开且有界子集，表示一个3D物体，如果知道\part \Omega的完整信息（即表面点和法向量），我们可以仅利用这些信息来表达\Omega的指示函数，of course！

定理3.1 高斯公式

假设 Ω 是 \mathbb{R}^3 中的一个 开且有界区域 (open and bounded region)，其边界 \partial \Omega 是光滑的，则：


F(x) = \int_{\partial \Omega} (\nabla \Phi (x - y)) \cdot v(y) \, dS(y)

其中：

v(y) 是 y \in \partial \Omega 处的 外法向量 (outward normal vector)。
\Phi(x) 是 三维拉普拉斯方程 (Laplace Equation) 的基本解。（我的感觉就是个核函数

Φ(x−y)⋅v(y) 计算 每个边界点 y 处的法向信息在 x 处的贡献。

指示函数

指示函数F(x)可以通过高斯函数表示如下：


F(x) =
\begin{cases}
0, & x \in \bar{\Omega}^c \quad \text{(外部，不属于)}\\
1/2, & x \in \partial \Omega \quad \text{(边界)}\\
1, & x \in \Omega\quad \text{(内部，属于)}
\end{cases}

在三维空间3D中，拉普拉斯方程的基本解为：


\Phi(x)=\dfrac{1}{4\pi |x|}

📌思考：我一开始对这里的高斯公式和指示函数有点晕，这个F(x)到底表示的是什么？

其实高斯公式提供了一种基于边界信息重建整个区域的方法，F(x)是高斯公式的结果，F(x)是通过高斯公式计算出来的。

（不恰当的）举例：

现在有一个篮球，我有表面的温度信息，我想知道内部球心的温度T(x)是多少，我可以通过表面放温度传感器记录局部温度T(y)，我可以通过这个来求。这个就是高斯公式的six，只用边界信息来推倒整个区域的信息。高斯公式的本质是一个积分方程

3.2 参数化高斯公式

原始的高斯公式：


F(x) = \int_{\partial \Omega} (\nabla \Phi(x - y)) \cdot v(y) \, dS(y)

当边界上的点集\mathcal{Y}=\{y_j\}_{j=1}^{N_Y}足够密集的时候，积分可以离散化为求和


F(x) \approx \sum_{j=1}^{N_Y} \frac{-(x - y_j)}{4\pi |x - y_j|^3} \cdot v(y_j) \, \sigma(y_j)

这里的v(y)是在y点的单位法线，而\sigma(y)是近似的局部表面积元素。

对于每一个y_j，(\nabla \Phi)(x-y_j)=-(x-y_j)/(4\pi|x-y_j|^3)是一个\mathbb{R}^3到\mathbb{R}^3的向量值径向基函数（RBF）。


\phi_j(x)=(\phi_{j1}(x),\ \phi_{j2}(x),\ \phi_{j3}(x)):=\dfrac{-(x-y_j)}{4\pi |x-y_j|^3}

\phi_j(x)仅由y_j确定，可以认为是基于y_j的径向函数，我们写到


\mu_j=(\mu_{j1},\ \mu_{j2}, \ \mu_{j3}):=v(y_j)\sigma(y_j)

这是y_j处的表面元素的近似值。我们简单称\mu_j为线性化表面元（LSE），而指示函数这时候可以表示为：


F(x) \approx \sum_{j=1}^{N_Y} \phi_j(x) \cdot \mu_j = \sum_{j=1}^{N_Y} \sum_{k=1}^{3} \phi_{jk} (x) \mu_{jk}

这说明高斯公式可以被看作是一个基函数的线性组合，未知系数是\mu_j

为什么是三个维度？

因为这是一个三维的向量（\mu_j等），每一个维度表示一个方向，例如\mu_j=(\mu_{j1},\mu_{j2},\mu_{j3})分别对应x,y,z三个方向，例如此时法向量指向外侧为(0,0,1)和表面积元素为\sigma(y_j)=0.1，那么此时的\mu_j=(0,0,0.1)

表面元就好像积分\int_{\partial \Omega} f(y)dA里面的dA，但是我们是数值计算，无法操作连续的积分，所以要用离散的点来近似计算，用有线个点来近似连续的表面积积分

对于上面的式子，原来的表面积分变成了一个离散的权重求和问题，即：


F(x) \approx \sum_{j=1}^{N_Y} \phi_j(x) \cdot \mu_j

这里\phi_j(x)是向量基函数，描述了y_j对x的影响

为了求解\mu_j我们选取了一个新的点集\mathcal{X}=\{x_i\}_{i=1}^{N_X}，也是位于表面上的一组点，从方程1和方程7可以得到以下线性约束：


\sum_{j=1}^{N_y} \sum_{k=1}^{3} \phi_{jk}(x_i) \mu_{jk} = \frac{1}{2}, \quad i = 1, \dots, N_X

这里已知的是：\phi_{jk}(x_i) \mu_{jk}，由高斯公式确定，由\phi_j(x)=(\phi_{j1}(x),\ \phi_{j2}(x),\ \phi_{j3}(x)):=\dfrac{-(x-y_j)}{4\pi |x-y_j|^3}得到

未知变量是\mu_{jk}

为了方便求解，我们可以写成矩阵形式


A\mu=b

当然这里的b:=(1/2,...,1/2)^T

我的理解，再回头看公式：


\begin{aligned}
F(x) &= \int_{\partial \Omega} (\nabla \Phi(x - y)) \cdot v(y) \, dS(y)\\
&\approx \sum_{j=1}^{N_Y} \textcolor{red}{\frac{-(x - y_j)}{4\pi |x - y_j|^3}} \cdot \textcolor{blue}{v(y_j) \, \sigma(y_j)}\\
&=\sum_{j=1}^{N_Y}\textcolor{red}{\phi_j(x)\cdot\textcolor{blue}{\mu_j}}\\
&=\sum_{j=1}^{N_Y}\textcolor{green}{\sum_{k=1}^{3}}\phi_{jk}(x)\mu_{jk}
\end{aligned}

这些都是三维的，所以需要求和，再理解一下就是因为\mathbb{R}^3进行点乘那么就是一个标量

接下来就是如何求解的问题了，太复杂了，我先不看了。在这一节的末尾也提出来了一些求解的困难。3.3中介绍了方程9的重新制定。