PointNet Conclusion
无序性
主要解决的是点云的无序性。例如点云数据(P_1,P_2,\cdots,P_n)和重新排列后的(P_3,P_1,P_5,\cdots,P_n)在点云是相同的,但是在神经网络中可能会是不同的输入。
主要任务
- 3D物体分类
- 3D语义分割
- 局部分割:输入是单个点云(飞机),预测每个点属于哪个部件,机翼机身
- 场景分割:输入是场景的一部分,预测每个点属于哪个类别
- 输出是
n\times m矩阵,n是点数,m是可能的语义类别数,每个点都有m维得分向量。
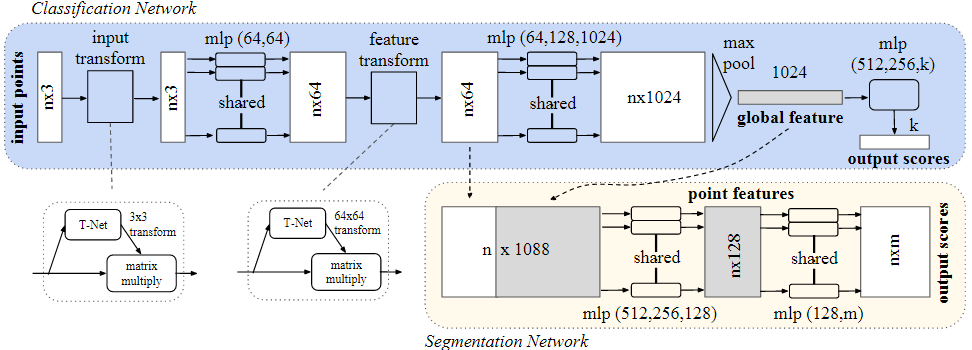
T-Net:
我所理解的T-Net主要是学习点云的空间变换矩阵,学习一种规则让其方向进行调整,类似于“矫正器”。因为一本倒着的书和竖着的书是不一样的,如果训练集中大多数书都是竖着的,那么这个网络可以学习如何让书竖起来,学习的是一种“规则”
PointNet++ Conclusion
PointNet Defect & PointNet++ Solution
-
忽略了局部特征
采用的是全局Max Pooling,把所有点的特征聚合成一个全局特征向量
-
对点的密度变化敏感
点云密度可能不均(近处密集,远处稀疏 或者 光滑表面点少)
直接在所有点上计算特征,无法适应点密度变化,导致对远处或稀疏区域的特征提取能力较弱
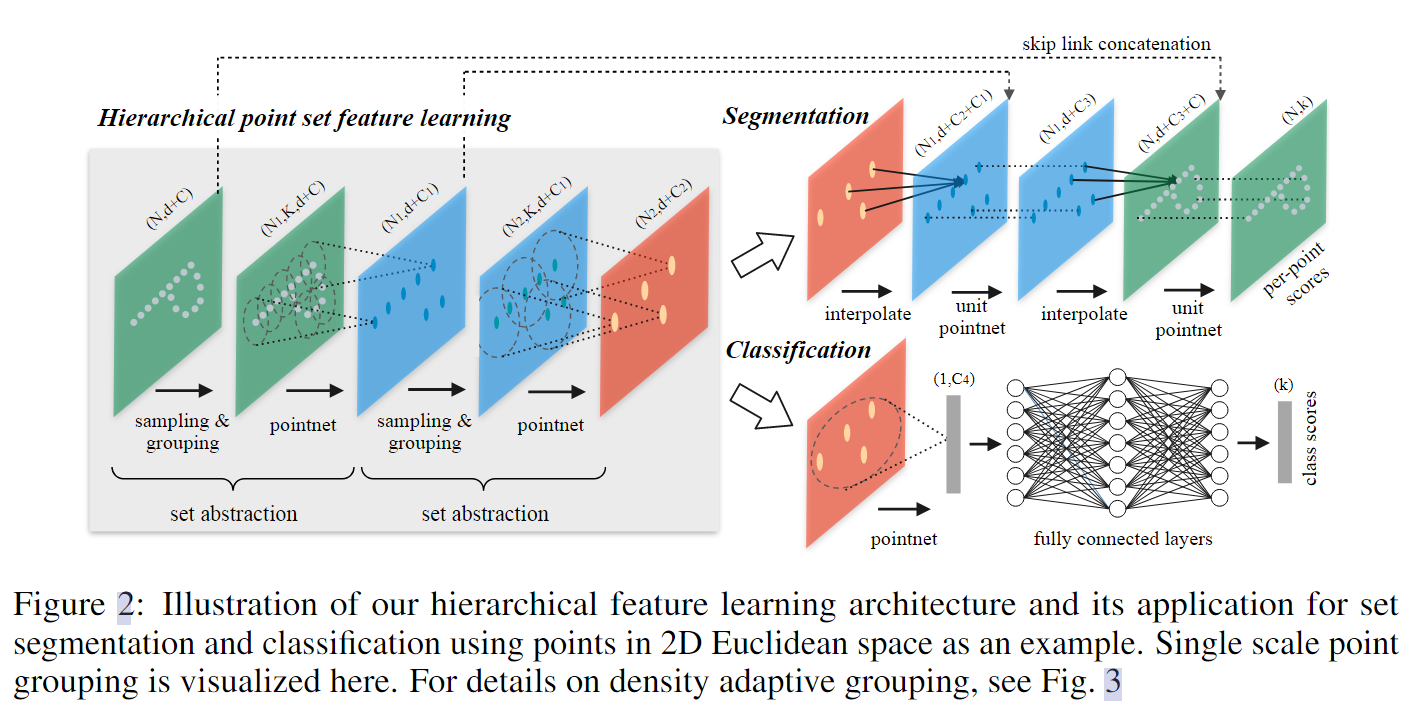
PointNet++ 通过 “层次化采样 + 局部特征提取” 来解决 PointNet 的问题:
1️⃣ 层次化特征学习(Hierarchical Feature Learning)
- 类似于 CNN 处理图像的方式,PointNet++ 采用 分层方法 逐步学习 局部到全局特征。
- 在低层,提取小范围的局部特征;在高层,提取更大的区域信息。
2️⃣ 自适应采样策略(Sampling & Grouping)
- 采用 Farthest Point Sampling (FPS) 进行 点云的层次化采样,确保采样的点均匀覆盖整个点云。
- 在采样的中心点周围,使用 球形搜索(Ball Query) 选择邻域点进行局部特征提取。
3️⃣ 局部特征学习(Local Feature Aggregation)
- 对于每个采样点,它的邻域点会通过 PointNet(共享 MLP) 计算一个局部特征。
- 这些局部特征会被进一步聚合,以学习更深层次的几何信息。
Some Question
Q:为什么需要Skip Link Concatenation?
因为在逐步采用的过程中,部分细节信息可能会丢失,所以需要拼接,在每个点高层恢复的时候,仍然保留了底层信息
Q:为什么叫unit pointnet
因为unit pointnet是一个小型的pointnet结构,共享MLP和最大池化
Q:可以点云降噪吗?
GPT说可以,可以进行异常点的检测,如果一个点是噪声点,它的领域特征往往会很弱,特征传播可以平滑点云
Say something
我谈一谈我的理解:
pointnet是开创性的,主要获得全局的特征,那么这篇pointnet++就是可以获取局部特征的网络,首先分成若干个patch,例如1024分成256个,按照距离划分(如上图Figure 2)可以重叠,例如一开始点云X是有1024个点,那么我用FPS(最远距离)进行采样得到256个patch,每一个patch可以有50个。
那我们举例子首先是一个飞机,它有很多机翼、机头、尾翼等,那么我这一次的操作会获取机翼上的某一个边缘,也会有另外一个边缘的patch,这样学习特征。
那么学习完边缘这种小的特征之后呢?我就要继续再分,我256再使用FPS采样成64个,那么经过这一个融合可能几个边缘会成一个机翼,那么我就学习到的机翼的特征,同样我也有尾翼和机头的特征。那么一直这样下去,64变16变4(注意不能只剩下一个)最后学习到了很多的特征。这就是学习的过程
Q:图2右边的分割是什么样的呢?
A:可以注意到这里有interpolate(插值),和KNN有关,那么我有了一些细分的特征,我可以通过插值让每个点都有特征值。
f^{(j)}(x)=\frac{\sum_{i=1}^{k} w_{i}(x) f_{i}^{(j)}}{\sum_{i=1}^{k} w_{i}(x)} \quad \text { where } \quad w_{i}(x)=\frac{1}{d\left(x, x_{i}\right)^{p}}, j=1, \ldots, C
对于是不是能够到4也是一种问题,比如我可以让其1024\rightarrow 256\rightarrow 64 \rightarrow 16,很容易理解如果只有四个点插值会出现一定的问题
Q:那么每个点的特征有什么用呢?
A:每个点都有特征,那么机翼里面的点会“相近”,尾翼里面的点会“相近”,这样就形成了分割。甚至如果有些点差别大,那么可以认为是噪声。“相近”可以用一些欧氏距离、余弦相似度等
Q:点云的无序性说明了什么
点云是无序的集合,这意味着点的排列不会改变它们代表的几何形状。这需要设计特征提取器和排列不变(permutation invariant)的损失函数。
