Information Geometric Framework for Comparing Point Clouds - 用于比较点云的信息几何框架

Abstract

1. 研究问题：将点云视为某个概率密度分布（PDF）上的样本，赋予点云空间统计流形结构，统计流形使得可以用信息几何工具来分析点云
2. 采用的方法：
   1. 使用高斯混合模型（GMM）计算点云的概率密度分布函数（PDF）
   2. 使用修改版的对称KL散度 来衡量两个点云的PDF之间的相似性

1. Introduction

• [x] 本文研究目标

  开发一个理论和计算框架，用于比较点云表示的对象

  利用信息几何工具，考虑点云的形状、结构、模式和整体分布

• [x] 提出的方法

  • 深度学习模型（DGCNN, FCNN）来学习点云的嵌入表示
  • 高斯混合模型（GMM）将点云映射到统计流形
  • 采用修改版呃KL散度

• [x] 点云的三个挑战：

  1. 点云没有固定的度量标准（点云是无序的，无法直接用欧几里得距离比较）

     如果是网格或者体素，我们可以直接对应点直接比较；但是点云是无序的，随机序列的，无法按照固定的索引找到

  2. 点云表示的是表面，而不是具体的点（点云是从表面采样的，不同点云即使是相同的物体，点的位置可能完全不同）

     A：1000个点，均匀分布在立方体表面；B：500个点，随机分布在立方体表面。虽然相同，但是点不完全对齐。

     我的理解：理想情况下A的1号点去和B的1号点进行计算，然后A的2号点和B的2号点去计算，但点云无法做到，这就是点对点

  3. 传统点云比较方法依赖点对应（Point Correspondence）。

     传统的方法如Hausdorff距离和Chamfer距离，依赖点与点之间的最近邻匹配，但是点云是随机采样的，点云密度不均匀的时候最近邻会失效，点云有噪声时会匹配到错误的等

     假设有两个点云，都表示一个圆：

     A：代表一个完整的；B：代表相同的，但少了一部分

     • Hausdorff距离计算最坏情况的最近邻距离，因为B少了一部分，但A中某些点找不到合适的匹配点，导致Hausdorff距离过大。虽然主要部分相似，但是这个距离认为它们非常不同。
     • Chamfer距离计算所有点的平均最近邻距离，会因为密度和噪声而不一样。

这里提一嘴KL散度：

KL(P\Vert Q)=\int p(x)\log\dfrac{p(x)}{q(x)}dx

本质上刻画了「若真实分布是P，用分布Q来解释数据时所造成的信息损失」。

因为分子分母调换就会改变积分的权重和被积函数，所以非对称

这个回答讲的特别好：https://www.zhihu.com/question/345907033/answer/3072696582

KL散度和Hausdorff距离和Chamfer距离对比

https://paste.org.cn/oK6f5knVFZ

有一些自己的理解：

1. Hausdorff距离可以放大差距，有一点的缺陷可以使其很大；而Chamfer距离则体现不出差异，因为平均而具有鲁棒性；但使用KL散度可以查看两个分布是否相似
2. 例如同样的圆形点云A和B，但B少了其中的六分之一圆弧，Hausdorff距离可以很大，而Chamfer距离小一些，但KL散度会有一个很大，这是因为无法看成同一个圆，这不是同一个物体
3. 如果KL散度都接近于一个较小的值的话，这表示可以认为二者是同一个物体

2. Related Works 相关工作

这里讨论了现有的点云比较方法，包括了

• Hausdorff 距离
• Chamfer 距离
• Earth Mover's Distance（EMD）
• Gromov-Hausdorff 距离

Hausdorff距离

关注两组点之间的最大最小距离，用于衡量最坏情况下的偏差

D_H(P, Q) = \max \left\{ \sup_{p \in P} \inf_{q \in Q} \|p - q\|, \sup_{q \in Q} \inf_{p \in P} \|p - q\| \right\}
\tag{1}

• P，Q是两个点云
• 寻找每个点p的最近点q，然后取最大值

局限性：

• 过于关注最坏情况，对局部缺陷过度敏感。
• 如果点云有少量噪声或采样误差，Hausdorff 距离可能会误判为极端情况。

Chamfer距离

Chamfer 距离计算所有点的最近邻距离的平均值，相比 Hausdorff 距离更加鲁棒（不易受极端点影响）。

CD(P, Q) = \frac{1}{|P|} \sum_{p \in P} \min_{q \in Q} \|p - q\| + \frac{1}{|Q|} \sum_{q \in Q} \min_{p \in P} \|p - q\|

• 计算P到Q的所有点的最近邻距离的均值
• 计算Q到P的所有点的最近邻距离的均值
• 取两个均值之和作为Chamfer距离

优点：

• 鲁棒性强，不像Hausdorff距离一样容易守个别异常点影响

局限性：

• 容易被点云密度不均匀所影响
• 如果一个点云的密度比另一个点高，最近邻匹配可能会失衡

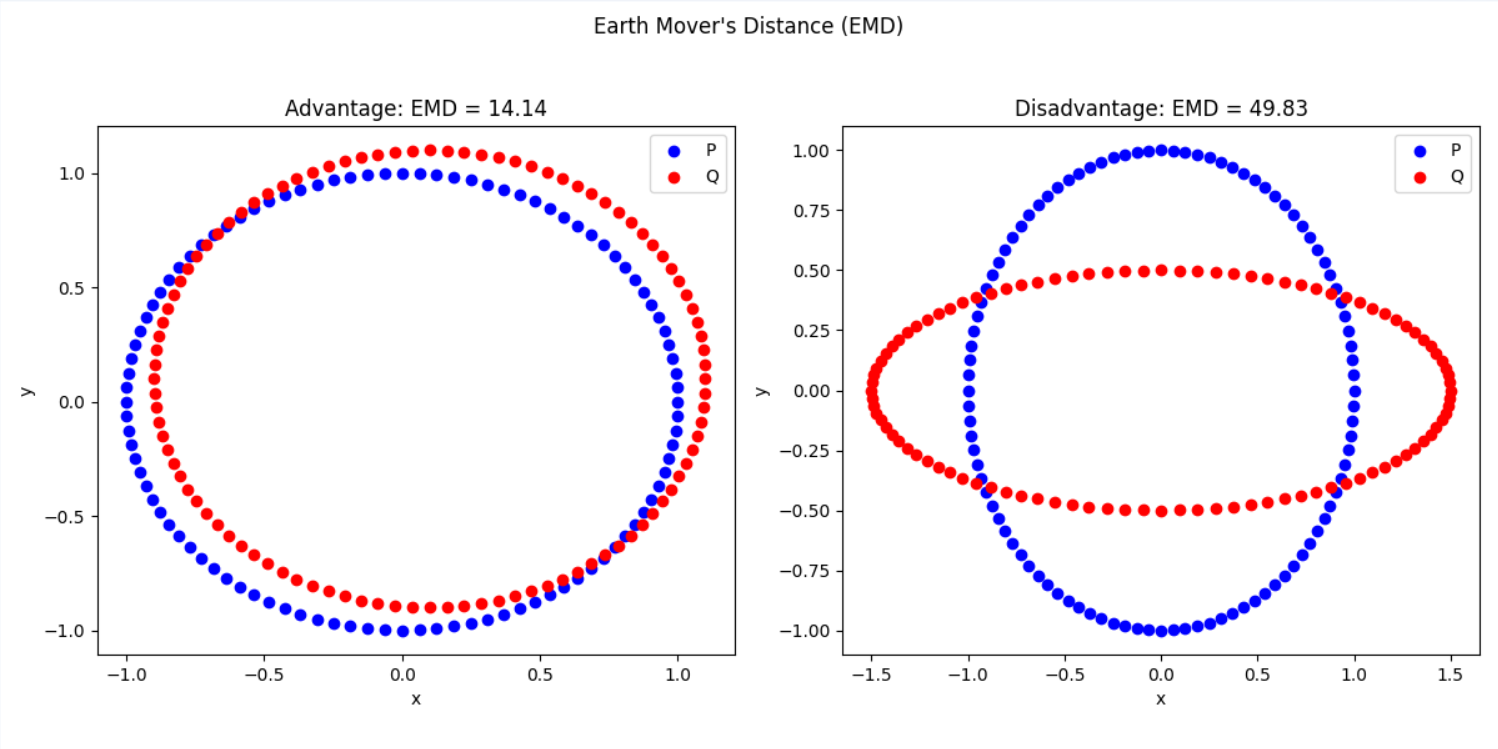
Earth Mover's Distance（EMD）

EMD计算将一个点云转换为另一个点云的最小代价，适用于形状匹配

EMD(A, B) = \min_{\phi : A \to B} \sum_{a \in A} \| a - \phi(a) \|

• \phi(a)是点云A到点云B的匹配函数（即照到最优点对应）
• 求解最优匹配，使得点云A变成点云B的成本最小化

优点：

• 适用于形状匹配，能够找到点云之间的最优变换

局限性：

• 开销大
• 不考虑整体形状结构

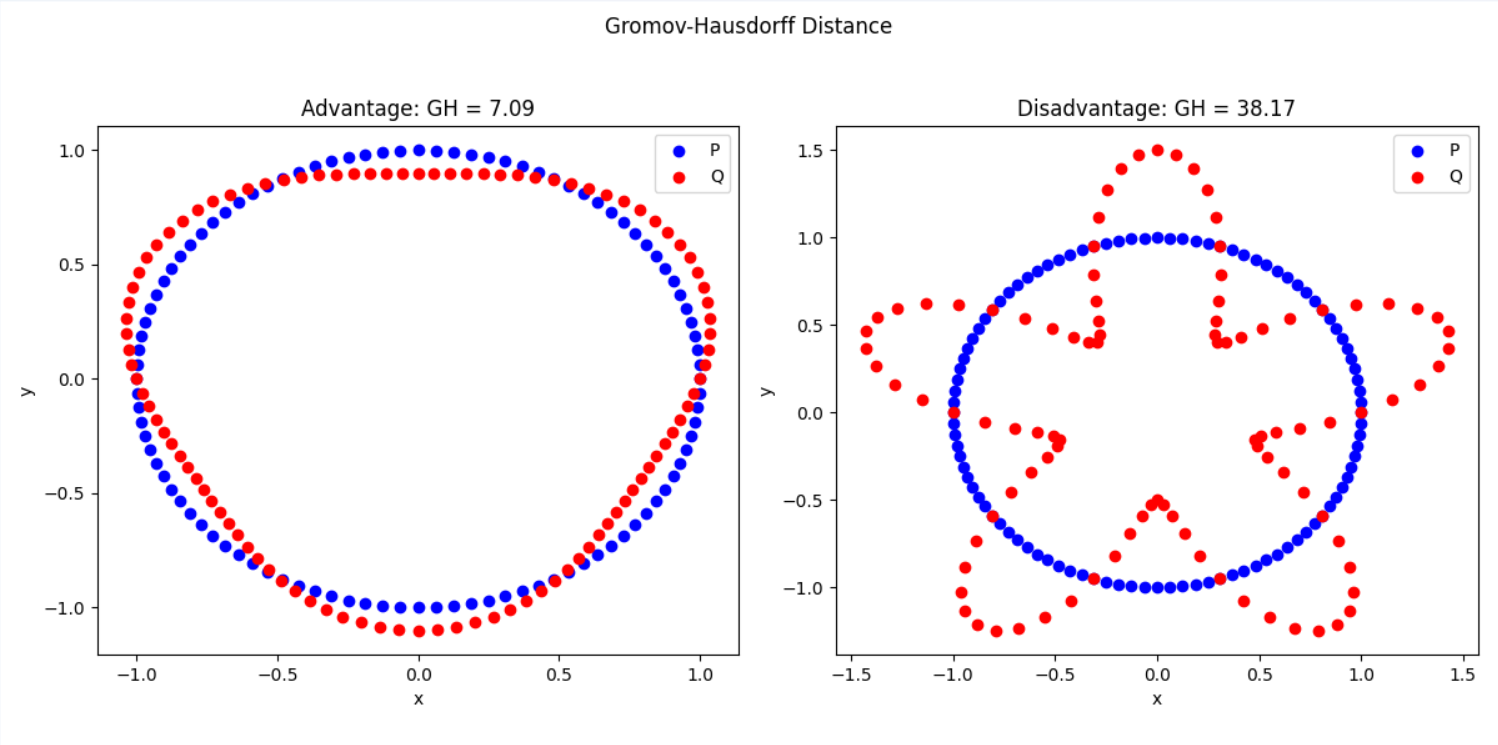
Gromov-Hausdorff距离

适用于非刚性匹配（如人体形变），用于度量两个点集嵌入到某个流形中的几何差异

d_{GH}(X, Y) = \inf_{Z, f, g} d_H^Z (X, Y)

• X,Y 是两个点云的子集。

• Z 是点云嵌入的流形。

• 核心思想：在某个共同的流形 Z 上，寻找两个点云的最优匹配。

优点：

• 适用于非刚性物体匹配，如人脸、人体、动物形状等复杂数据
• 提供了一种测度拓扑结构的方式

局限性：

• 计算复杂度高，需要寻找最佳嵌入流形Z
• 高维点云计算困难

📌 总结

方法	形象类比	适用场景	优势	局限性
Hausdorff 距离	破损篮球 vs. 完整篮球	最坏情况的偏差	适用于检测异常	对局部缺陷过敏感
Chamfer 距离	撒在地上的米粒	整体形状相似度	计算开销小	受点密度影响
EMD	移动土方	形状匹配	考虑最优点对应	计算量大
Gromov-Hausdorff	橡皮泥人 vs. 变形橡皮泥人	变形物体匹配	适用于非刚性匹配	计算代价高
信息几何方法（GMM + KL 散度）	不同风格的音乐	统计形状分析	鲁棒性强	需要概率建模

📌我的理解：

• Hausdorff距离：在乎最坏情况

  在乎最远点对的距离，如果有瑕疵距离都很大→哪怕是一个裂缝都会被认为是不同的物体

• Chamfer距离：在乎整体平均距离

  关注所有点的平均最近邻距离，就像米粒，不会因为一个掉远了而导致放大距离

• EMD：在乎点的搬运成本（形状匹配）

  关注如何“移动”点云使得尽量匹配，反应点云之间的最优匹配策略

  形象理解：如果A是一堆土，B是另一堆土，它计算从A变成B需要移动多少土方

  • 如果A和B只是轻微错位，EMD会找到一个低成本的匹配策略，距离小
  • 如果A和B形状差异很大，EMD需要搬运大量点，距离就会大
  

• Gromov-Hausdorff距离：在乎拓扑结构的相似性（适用于形变物体）

  • 特点：适用于非刚性匹配（人体形状、动物形状等，即使有些弯曲或者形变，仍然可以认为是同一个物体。
  • 形象理解：如果A是标准人形橡皮泥，B是用手按压的，距离还是会小，认为是同一个
  

分析四个距离的代码：https://paste.org.cn/5rvI7HlUxd

3. Information Geometry 信息几何

阅读材料：几何学中最伟大的发明之一——流形，其背后的几何直觉与数学方法

信息几何关注概率分布的结构，在参数空间上定义几何度量，可以在分布之间使用黎曼度量来衡量。（这些我懂，接下来有一些概念）

📖 拓扑流形：由一组满足一定条件的开集组成

统计流形是一个拓扑空间，具有以下属性

1. 空集和整个集合是开集
2. 有限个开集的交集仍然是开集
3. 任何开集的并集仍然是开集

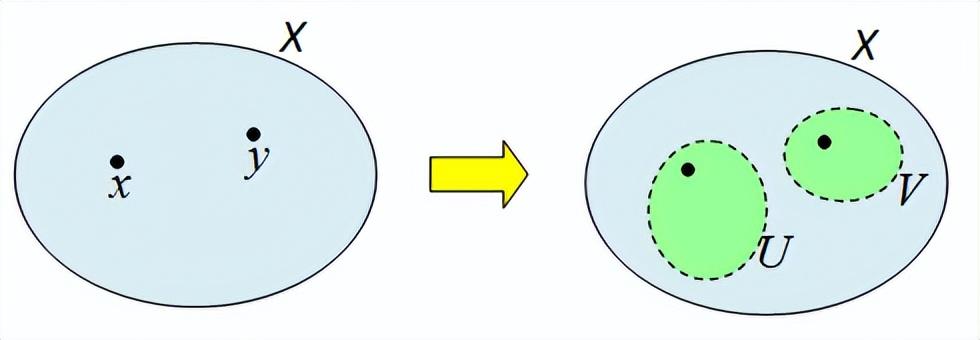
📌 Hausdorff 性质：

• 如果拓扑空间满足Hausdorff 条件，即任意两个不同的点都能被两个不相交的开集分开，那么这个空间的点是可区分的。
• 这意味着统计流形上的每个概率分布都可以被唯一地识别。
• 豪斯多夫空间（如下图）

📌 第二可数性（Second Countable）：

• 如果拓扑空间的拓扑基是可数的，那么它是第二可数的。
• 这意味着，统计流形上的任何概率分布都可以用有限的参数来表示。

这里引发了我的一些思考：

1️⃣ 什么是开集？为什么总要强调开集？

思考：不包含边界的，如(1,2)就是，但[1,2]就不是。为什么总要强调开集呢？
因为要保证拓扑空间具有良好的局部性质，换句话说，对于集合中的任意一点，你都可以在该点的周围找到一个小范围的区域，它仍然在这个集合里面，这样可以做一些连续变化、微积分等运算。

---

2️⃣这里说的“整个集合”是什么？

说的就是1D中的\mathbb{R}以及2D中的\mathbb{R}^2等，空集当然也是开集

---

3️⃣ Hausdorff 性质是什么？为什么重要？

一个拓扑空间是Hausdorff空间，对于任意两个不同的点x,y，都存在两个不相交的开集来分别包含x,y。

我认为最重要的地方就是在于可区分！这对于拓扑度量至关重要，在统计流形上这意味着两个不同的概率分布可以被清楚地区分，而不是混杂在一起。

---

4️⃣ 第二可数性是什么？有什么作用？

可数基意味着我们可以用有限的信息描述整个拓扑空间，这使得数学运算（度量、测地线）更容易处理。

在信息几何中，统计流形的第二可数性意味着可以用有限维参数化的概率分布来表示整个流形，而不需要无限复杂的描述，计算Fisher信息矩阵和度量更加高效（作用：简化计算）

使用GMM和KDE进行分析的代码https://paste.org.cn/UrezDiTCeR

3.1 Smooth Manifold 光滑流形

一个n维拓扑流形M是一个：

1. 第二可数(Second countable)的拓扑空间 → 可以用有限的参数来表示
2. Hausdorff空间 → 任意两个不同的点可以被分开
3. 局部欧几里得空间(Locally Euclidean) → \mathbb{R}^n

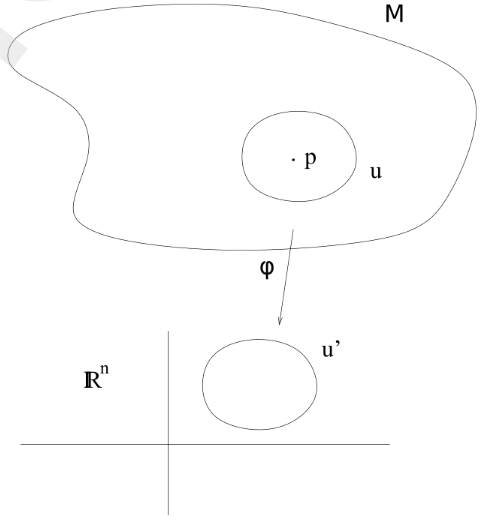
具体来说，对于流形上的每一个点p\in M，存在一个局部开集U\subset M和一个同胚映射（homeomorphism）\phi: U\rightarrow U^\prime，其中U^\prime是欧几里得空间\mathbb{R}^n中的开集。这个局部坐标图(U,\phi)就称为流形上的坐标图（coordinate chart）

📌 直观理解

对于地球表面来说，地球是一个球面，但是在一个小区域例如北京，在这里看起来就像一个平面（2D欧几里得空间）

一个三维物体的表面，局部区域看起来就是一个二维平面

📌 同胚

同胚是一种特殊的映射，要求\phi是双射(bijective)、连续的，且它的逆映射F^{-1}也必须是连续的。

如果我们在流形M上有两个坐标图(U,\phi)和(V,\phi) ，并且它们有重叠区域U\cap V\neq \emptyset，那么可以定义一个过渡映射(transition map)：

\psi \circ \varphi^{-1}:\varphi(U\cap V)\rightarrow \psi(U\cap V)

这个映射表示如何在不同的坐标图之间转换。

📌 图表和图集

图表(chart)：是从一个流形的开子集映射到欧几里得空间的开子集，换句话说一个图表告诉你它试图将哪个平面展开以及如何展开

图集(atals)：可以用一组图表来覆盖整个流形

图表重叠：虽然肯定可以设计出不重复的图表，但是往往很困难，所以只要不发生矛盾我们就允许其重叠。为了确保没有矛盾，我们说如果两个图表覆盖了同一个点，那么应该有一种方法可以从其中一个图表到达另一个图表，反之亦然。执行这种转换的函数称为过渡映射（transition map）换句话说，过渡映射将我们从一个图表上的一个点带到另一个图表上的一个点。

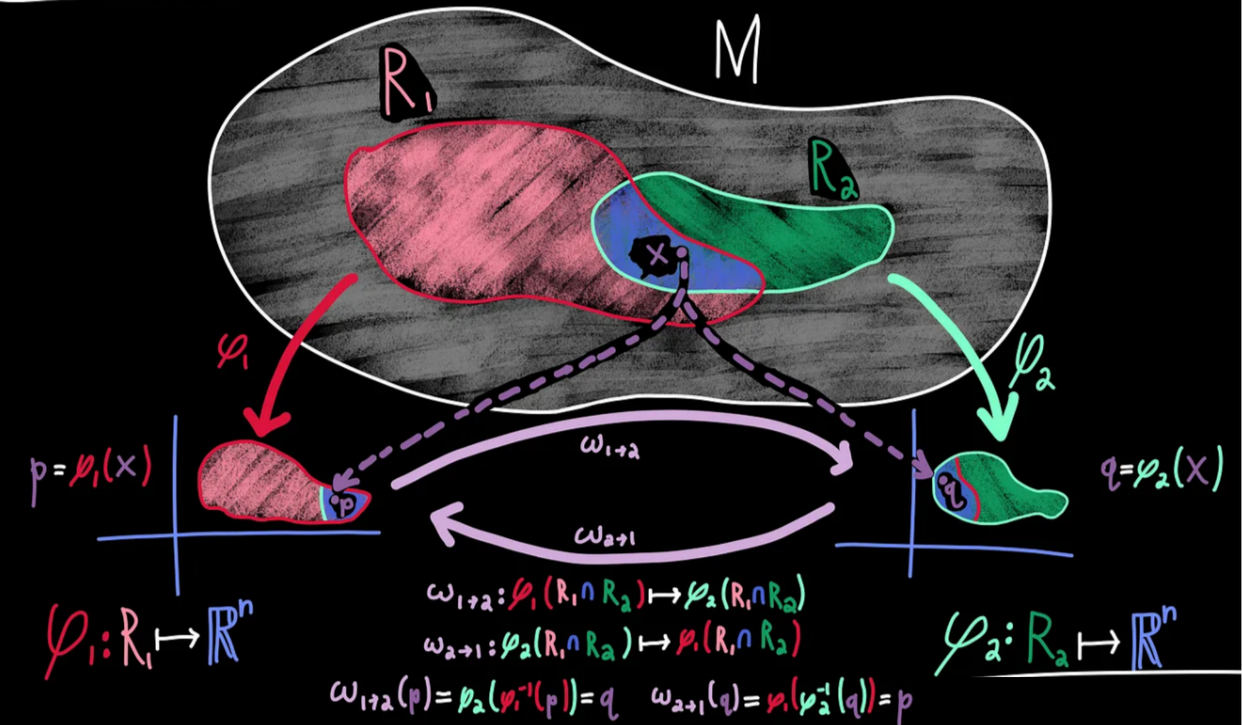
直观上来看，过渡映射就像是不同地图之间的转换，描述了如何从一个坐标系转换到另一个坐标系。

如果两个坐标图满足以下条件之一：

1. 它们没有重复U\cap V=0
2. 过渡映射是微分同胚的(diffeomorphism)（即可微且可逆）

那么我们称它们是smoothly compatible 光滑兼容.

如果一个坐标图的集合A可以覆盖整个流形M，那么这个集合称为图集(atlas)

不同国家的地图拼起来覆盖整个地球。（可以重叠）

微分同胚要求坐标转换不会引入奇异点或者不连续性

一个流形M到实数的函数f:M\rightarrow \mathbb{R}被称为光滑函数，如果在任何坐标图(U,\varphi)上，转换后的函数f\circ \varphi^{-1}是光滑的（可微分）。所有从M到\mathbb{R}耳朵光滑函数的集合记作C^\infty (M)，并构成一个实向量空间。

📌 如何理解这里的f\circ \varphi^{-1}？如何理解这个\circ符号？

\circ表示函数的复合，例如如果有两个函数

• g:A\rightarrow B
• f:B\rightarrow C

那么它们的复合函数f\circ g:A\rightarrow C定义为：

(f\circ g)(x)=f(g(x)),\quad \forall x\in A

先用右侧的g作用于x得到g(x)，再用f作用于g(x)得到最后的f(g(x))。

---

那么对于f\circ \varphi^{-1}进行分析，已知：

• f:M\rightarrow \mathbb{R}，是定义在流形上的函数
• \varphi:U\subset M\rightarrow \mathbb{R}^n，是一个局部映射
• \varphi^{-1}:\mathbb{R}^n\rightarrow M，是反向映射

那么f\circ \varphi^{-1}作用就是：

(f\circ \varphi^{-1})(x)=f(\varphi^{-1}(x))

这意味着：

1. 首先\varphi^{-1}首先作用于局部欧几里得空间，将坐标转换为流形上的点p
2. 然后用f作用这个点，得到最终的数值\mathbb{R}

我们可以在欧几里得空间中研究流形上的函数

在流形M上的某个点p，切空间T_pM是所有在该点p处的导数运算集合。导数运算满足Leibniz规则的线性映射。

一个黎曼度量（Riemannian metric）g是定义在流形上的光滑、对称、正定的2-阶张量场，用于测量切空间中的内积：

g_p:T_pM\times T_pM\rightarrow \mathbb{R}

在欧式空间中，黎曼度量就是普通的内积

但是在球面上，不同位置的度量可能不同，例如维度越高，东西方向上的测度就越小

3.2 Statistical Manifold 统计流形

假设(X,\Sigma, p)是一个概率空间，其中\mathcal{X}\subset \mathbb{R}^n。我们考虑一族定义在\mathcal{X}上呃概率分布集合\mathcal{S}。假设\mathcal{S}中的每个元素都可以由n个实数变量\theta =(\theta^,\cdots, \theta^n)参数化，即

\mathcal{S} = \{ p_{\theta} = p(x; \theta) \mid \theta = (\theta^1, ..., \theta^n) \in \Theta \}

其中，\Theta是\mathbb{R}^n的一个开子集，映射\theta ↦ p_\theta是打死你和（即不同的\theta产生不同的概率分布）。这个概率分布族\mathcal{S}被称为n为统计流形或参数模型，我们通常写作\mathcal{S}=\{p_\theta\}。

对于模型\mathcal{S}=\{p_\theta \mid \theta\in\Theta\}，定义从\mathcal{S}到\mathbb{R}^n的映射

\varphi(p_{\theta}) = \theta

它允许我们用\phi(\theta^i)作为\mathcal{S}的坐标系。

这意味着我们可以把一个概率分布p(x;\theta)映射到它的参数\theta。在正态分布里\varphi(p_{\mu,\sigma})=(\mu,\sigma)这说明我们可以用(\mu,\sigma)来作为坐标来描述这个统计流形。例如泊松分布里面的参数只有\lambda，那么统计流形只有一维\theta=\lambda，是一个一维微分流形。

假设存在一个 C^\infty 微分同胚（diffeomorphism）\psi : \Theta \to \psi(\Theta)，使得 \psi(\Theta) 仍然是 \mathbb{R}^n 的一个开子集。那么如果我们用新的参数 \rho = \psi(\theta)代替 \theta，则统计模型可以表示为：

\mathcal{S} = \{ p_{\psi^{-1}(\rho)} \mid \rho \in \psi(\Theta) \}

这表明概率分布族 \mathcal{S} = \{ p_{\theta} \} 构成了一个统计流形（statistical manifold），即一个 C^\infty 微分流形。

📌切空间(Tangent Space)

在某个点p_\theta处，统计流形\mathcal{S}的切空间T_\theta(\mathcal{S})由以下向量张成：

\left\{ \frac{\partial}{\partial \theta^i} p_{\theta} \mid i = 1, ..., n \right\}

这表明统计流形上的切空间由参数的变化率张成。

得分函数定义为：

\frac{\partial}{\partial \theta^i} \log p(x; \theta)

记作\partial_i\ell(x;\theta)

Fisher 信息度量 (Fisher Information Metric)

在统计流形上，我们可以通过如下方式定义自然的黎曼度量

g_{ij}(\theta) = \mathbb{E}_{\theta} [\partial_i \ell(x; \theta) \partial_j \ell(x; \theta)]

也可以写成：

g_{ij}(\theta) = \int \partial_i \ell(x; \theta) \partial_j \ell(x; \theta) p(x; \theta) dx

📌对于得分函数和信息度量的理解：

• 得分函数

\frac{\partial}{\partial \theta^i} \log p(x; \theta)

本质上，它是对数似然函数\log p(x;\theta)对参数\theta的偏导数，如果改变\theta那么数据点x的概率p(x;\theta)会如何变化。就好像对于f(x;a)=a\log (x)，我们对于参数a进行求偏导，f(x;a)会如何变化。

那么得分函数值越大，说明数据点x对于参数\theta就很敏感；反之，如果越小，那么就越不敏感。

再举一个例子，我们的正态分布，有参数\mu,\sigma:

 p(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left( - \frac{(x - \mu)^2}{2\sigma^2} \right)

对于均值\mu，得分函数是

 \frac{\partial}{\partial \mu} \log p(x; \mu, \sigma) = \frac{x - \mu}{\sigma^2}

这表明，如果x远离均值\mu，那么得分函数会越来越大，表示参数\mu变化对分布影响较大

• 如何理解上面这句话呢？

  现在很多x都聚集在\mu附近，那么稍微移动\mu不会有太大的影响，但是会对于远离\mu的值有很大的影响。

---

我们先看第一个式子，Fisher信息度量的定义，期望形式的：

 g_{ij}(\theta) = \mathbb{E}_{\theta} [\partial_i \ell(x; \theta) \partial_j \ell(x; \theta)]

Fisher信息度量衡量的是参数\theta的不确定性，它衡量如果参数发生微小变化，分布p(x;\theta)如何改变。这里乘积的意义涉及两个方向i,j的得分函数乘积：

• 当i=j的时候，表示\theta^i方向上自身变化的影响

• 当i\neq j的时候，表示两个方向上的相互作用，即\theta^i和\theta^j之间的影响

  Fisher信息度量：

• 对角项g_{ii}衡量的是参数\theta^i方向上的信息量

• 非对角项g_{ij}衡量不同参数之间的影响

  例如对于正态分布p(x;\mu,\sigma)，Fisher信息度量矩阵为：

 G(\theta) =
 \begin{bmatrix}
 \frac{1}{\sigma^2} & 0 \\
 0 & \frac{2}{\sigma^2}
 \end{bmatrix}

\frac{1}{\sigma^2}表示参数\mu方向上的信息量；\frac{2}{\sigma^2}表示参数\sigma方向上的信息量；非对角线为，表示\mu和\sigma之间无相关性。

🔍如何理解这个期望？

如果我们只计算一个样本x的得分函数乘积，那么可能会导致结果不稳定，所以需要对所有可能的x计算期望值，得到平均情况下的敏感度。

---

再来看第二个式子，积分形式：

 g_{ij}(\theta) = \int \partial_i \ell(x; \theta) \partial_j \ell(x; \theta) p(x; \theta) dx

我起初觉得这个公式很像测地线，实际上好像并不是，其实就是连续型随机变量的数学期望转换而来，其实就是：

 \mathbb{E}(x)=\int xf(x)dx

只不过这里的随机变量不是x，而是得分函数\dfrac{\partial \ell}{\partial \theta}

🔍那么测地线在何处呢？

测地线计算的公式需要用到F-R公式：

 d_{FR}(\theta_1, \theta_2) = \int_0^1 \sqrt{ g_{ij}(\theta(t)) \frac{d\theta^i}{dt} \frac{d\theta^j}{dt} } dt

需要很多的g_{ij}进行累计得到测地线，g_{ij}描述的是局部的几何结构

🔍那么既然是单个局部的g_{ij}，那么为什么是积分？

因为x是样本数据的随机变量，这个积分并不是计算一个特定的x，而是对所有可能的x进行加权求和。

例如：现在抛硬币有两种可能：

• x=0（反面），概率p(0;\theta)=1-\theta

• x=1（正面），概率p(1;\theta)=\theta

  那么Fisher信息度量就是一个离散求和

 g(\theta) = \sum_{x \in \{0,1\}} \left(\frac{d}{d\theta} \log p(x; \theta) \right)^2 p(x; \theta)

这里就是所有的x，其实也就是一直和期望相关，并不由单个的x决定。

🔍好像还和方差和协方差有关？

• 当i=j的时候，公式g_{ij}(\theta) = \mathbb{E}_{p(x;\theta)} \left[ \frac{\partial \ell(x; \theta)}{\partial \theta^i} \frac{\partial \ell(x; \theta)}{\partial \theta^j} \right]就变为了

   g(\theta) = \mathbb{E} \left[ \left( \frac{\partial \ell}{\partial \theta} \right)^2 \right]

而方差为：

   \operatorname{Var}[X] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2

考虑得分函数为0（稍后再讲），那么有\mathbb{E} \left[ \frac{\partial \ell}{\partial \theta} \right] = 0

所以：此时方差\operatorname{Var}[X]=\mathbb{E}[X^2] - 0=g(\theta)。这个时候就是方差

• 当i\neq j的时候，

   g_{ij}(\theta) = \mathbb{E} \left[ \frac{\partial \ell}{\partial \theta^i} \frac{\partial \ell}{\partial \theta^j} \right]

此时衡量的是参数\theta^i和\theta^j之间的相互作用，类似于协方差。

• 如果g_{ij}=0那么说明\theta^i和\theta^j二者相互独立。

  🔍那么为什么得分函数的期望为0？

  从概率分布p(x;\theta)的归一化条件开始：

   \int p(x; \theta) dx = 1

对参数\theta求偏导并且交换积分和导数：

 \int \frac{\partial}{\partial \theta} p(x; \theta) dx=\frac{\partial}{\partial \theta} \int p(x; \theta) dx = 0

由得分函数的定义出发，有：

 \frac{\partial}{\partial \theta} \log p(x; \theta) = \frac{1}{p(x; \theta)} \frac{\partial}{\partial \theta} p(x; \theta)

代入得到：

 \begin{aligned}
 \int p(x; \theta) \frac{\partial}{\partial \theta} \log p(x; \theta) dx &= \int \frac{\partial}{\partial \theta} p(x; \theta) dx = 0
 \\
 \mathbb{E} \left[ \frac{\partial \ell}{\partial \theta} \right] &= 0
 \end{aligned}

如果期望值等于意味着在整个数据分布情况下，正负影响相互抵销，好比一个班的成绩符合正态分布，统计所有人比平均分高多少（有正负），结果一定为0

好，现在进行的是KL散度(Kullback-Leibler Divergence)

在统计流形上希望能够定义两点（即两个概率分布）之间的“距离”，散度是一种衡量概率分布之间差异的函数。

KL散度用于衡量两个概率分布p(x;\theta_1)和q(x;\theta_2)之间的差异，定义如下：

D_{KL}(p \| q) = \int p(x; \theta_1) \log \frac{p(x; \theta_1)}{q(x; \theta_2)} dx

注意⚠️：

• KL散度不对称，即通常D_{KL}(p \| q)\neq D_{KL}(q\| p)

对称KL散度(Modified Symmetric KL Divergence)

我们可以定义修正的对称KL散度D_{MSKL}：

D_{MSKL}(p \| q) = \frac{1}{2} \left( D_{KL}(\sqrt{p} \| \sqrt{q}) + D_{KL}(\sqrt{q} \| \sqrt{p}) \right)

4. Information Geometric Framework for Point Clouds

这里建立一个统计流形框架来表示点云数据，点云输举由n个点组成，定义为:

X = \{x_1, x_2, ..., x_n\}, \quad x_i \in \mathbb{R}^m

4.1 Covering in the Context of Point Clouds（点云的覆盖概念）

在拓扑学中，覆盖的概念是用较小的子集去表示一个整体，在点云的上下文中，覆盖指的是用以组小区域来表示整个点云。

比如对于一个城市的地图，我无法直接刻画所有的细节，但是我可以划分成很多的街道然后分别测绘出这些区域。

将点云划分成多个子集U_1,U_2,...,U_k，每个子集代表一个局部区域，子集的并集覆盖整个点云X \subseteq \bigcup_{i=1}^{k} U_i

两个性质：

1. Locality（局部性）：对于每一个子集U_i\subseteq X，都存在一个在X中包含U_i的开集N_i。数学表达：U_i \approx N_i \cap X
2. Overlap（重叠）：不同子集可以有重叠部分，来确保数据在边界平滑过渡

4.2 Statistal Manifold Representation（统计流形表示）

选择有限的子集，简化点云X，同时保留关键功能。使用高斯混合模型（GMM）尤其重要。

4.3 Gaussian Mixtrue Model（高斯混合模型）

我应该在哪个地方好好研究了这个，我现在对于这里有足够的了解了，好像是在论文《A Statistical Manifold Framework for Point Cloud Data》中

对于一个点云，我可以用若干个高斯分布进行描述，比如我可以用一个高斯分布来描述桌面，用另外一些高斯分布来描述桌腿，这样这个桌子的整体形状就不再是点云的形式了而是由多个高斯分布组合而成。

GMM的参数

在GMM中，每个点x被认为是从K个高斯分布之一生成的：

\Theta = \{ (\mu_k, \Sigma_k, \pi_k) : k = 1, 2, ..., K \}

其中：

• \mu_k表示高斯分布的均值（中心）

• \Sigma_k表示高斯分布的协方差矩阵（形状和尺度）

• \pi_k表示高斯分布的混合系数（权重）

  \sum_{k=1}^{K} \pi_k = 1, \quad 0 \leq \pi_k \leq 1

而单个高斯分布函数的概率密度为：

\mathcal{N}(x | \mu_k, \Sigma_k) = \frac{1}{\sqrt{(2\pi)^m |\Sigma_k|}} \exp \left( -\frac{1}{2} (x - \mu_k)^T \Sigma_k^{-1} (x - \mu_k)\right)

• x：点云中的一个数据点。

• \mu_k：第 k 个高斯分布的均值（表示中心点）。

• \Sigma_k：第 k 个高斯分布的协方差矩阵（表示形状和尺度）。

• |\Sigma_k|：协方差矩阵的行列式，表示该高斯分布的扩展程度。

• m：数据的维度。

这个x我一开始误解了，不知道是在做什么，其实这个就是已知分布函数来求解x处的概率密度函数，如果这个点属于这个族，那么它的概率密度就大。这个高斯分布和我们以前学的2维的函数一样，只不过这个不是二维罢了。

注意，这只是单个，我们对其进行加权和才是整个GMM，即

p(x; \Theta) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x | \mu_k, \Sigma_k)

有一个比较形象的例子，就是我们来描述一个地形图，我们对于每一个山丘（簇）可以用一个高斯分布表示，通过调整不同山丘的大小（\Sigma_k）和位置（\mu_k）来改变整体的分布，多个山丘叠加在一起形成整个地形的分布。

4.4 Manifold Structure for Point Clouds

这里目的是将点云的空间Z赋予统计流形结构，点云X每个点x_i都是属于欧几里得空间，并且本质上离散的，我们用一个概率密度来表示这些点云数据，这里有GMM给出即：

p(x,\Theta)

其中参数\Theta是点云分布的参数，包括均值、协方差矩阵和混合系数（权重）,权重满足\sum_{i=1}^{K} \alpha_i = 1

T = \{\Theta = (\mu_1, ..., \mu_K, \Sigma_1, ..., \Sigma_K, \alpha_1, ..., \alpha_K) \}

这样可以认为所有点云的概率分布p(x,\Theta)构成了统计流形\mathcal{S}。

Theorem 1

如果两个GMM相等需要满足什么样的条件呢？定义两个GMM分别用p(x,\Theta_1)和p(x,\Theta_2)表示：

p(x, \Theta_1) = \sum_{i=1}^{K} \alpha_i \mathcal{N}(x; \mu_i, \sigma_i^2)
\\
p(x, \Theta_2) = \sum_{j=1}^{L} \beta_j \mathcal{N}(x; \nu_j, \tau_j^2)

需要满足：

p(x, \Theta_1) = p(x, \Theta_2), \quad \forall x

即：

1. 簇数相等K=L
2. 对应参数相等：权重、均值、方差

证明首先对GMM按照方差大小递增排序，然后观察x\rightarrow \infty时候主要由最大的方差项支配，进行分析并重复

Theorem 2

高斯混合模型（GMM）的参数空间T是一个拓扑流形。参数空间T定义如下：

T=\{\Theta  (\mu_1,...,\mu_k,\Sigma_1,...,\Sigma_K,\alpha_1,...,\alpha_k):\mu_i\in\mathbb{R}^m,\Sigma_i\text{是一个对称矩阵},\sum_{i=1}^K\alpha_i=1\}

其他不过多解释了，都讲到这里了，没什么好说的

一个参数空间的独立维度：

\dim(T) = K \left( m + \frac{m(m+1)}{2} \right) + (K-1)

为什么是这个数值呢？其实很好理解，我们分别对参数空间里面的\mu、\Sigma以及\alpha进行分析：

• \mu_i也就是数据点的维度，例如一个2维数据，那么此时m=2
• \dfrac{m(m+1)}{2}其实就是\Sigma_i对称矩阵的半边，如果是一个m=3的矩阵，那么上三角矩阵个数就是3+2+1=6个。
• 最后的K-1就是和\alpha_i有关，因为有限制和为1，那么自由度就是K-1，因为选取了前面的K-1个那么最后一个无法做出任何改变，就是余下的值

Theorem 3

映射h:T\rightarrow S由h(\Theta)=p(x;\Theta)定义，其中\Theta\in T。在多维高斯分布的协方差矩阵是对角矩阵的条件下，该映射是单射（即可逆的）

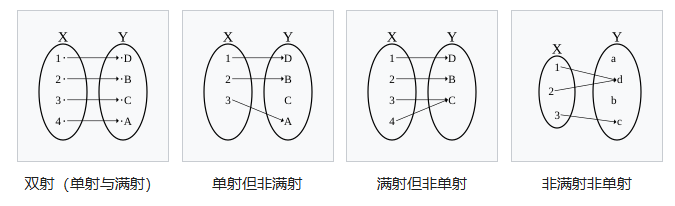
满射（Surjective）：值域y是满的，每一个y都有x对应（输出可以重复，但y要满）

单射（Injective）：输出无重复

双射（Bijective）：既是满射又是单射。每一个y都有x对应，且一一对应

5. Data

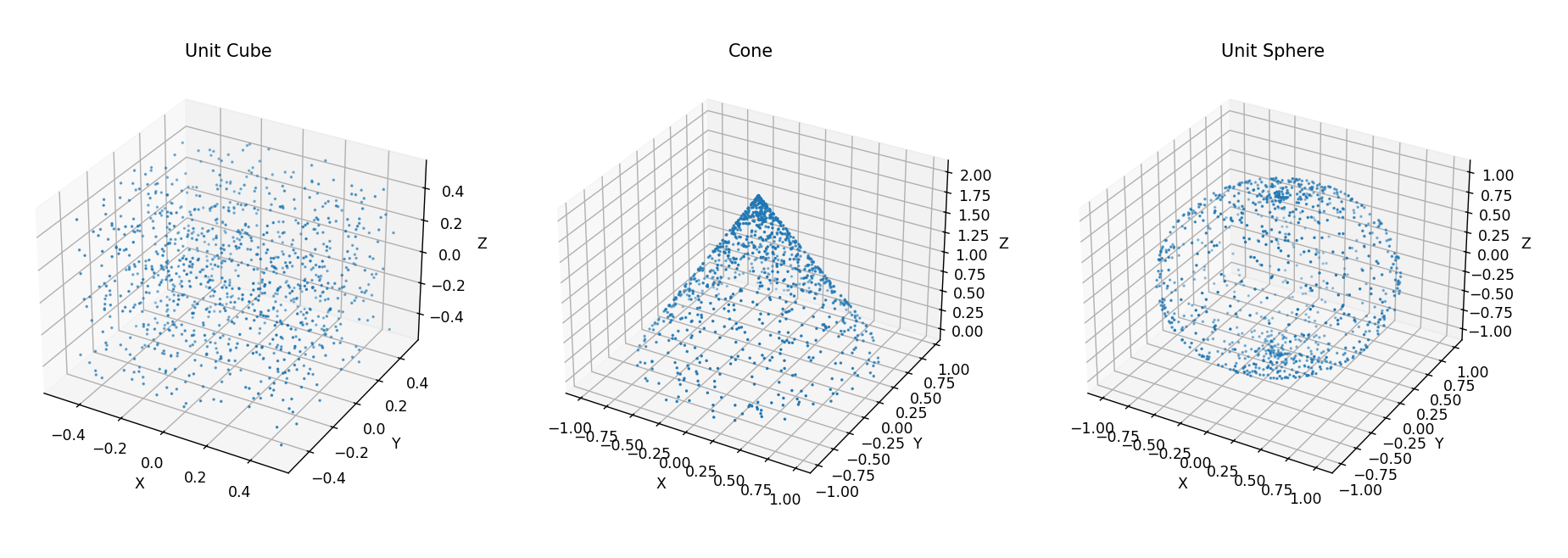
采样总结

在此研究中，我们考虑了三种基本的几何形状：单位立方体（U）、圆锥（C）和单位球体（S），并将其处理为点云数据。以下是每种形状的采样方法：

• 单位立方体 U:

单位立方体的定义：

-0.5 \leq x,y,z \leq 0.5

每个点 p_i 的坐标 (x_i, y_i, z_i) 都是 在范围 [-0.5, 0.5] 内均匀随机生成的。

• 圆锥 C:

圆锥体的点云数据采用 柱坐标系 (r_i, \theta_i, h_i) 表示：

• 角度 \theta_i 均匀分布在 [0,2\pi]。
• 高度 h_i 均匀分布在[0,2]。
• 半径 r_i 计算方式为： r_i = 1 - \frac{h_i}{2} 这个公式确保圆锥体在底部 (h=0) 具有最大半径r=1，而在顶部 (h=2) 逐渐收缩到 r=0。

然后，柱坐标系被转换为 笛卡尔坐标系 (x_i, y_i, z_i)：

x_i = r_i \cos(\theta_i), \quad y_i = r_i \sin(\theta_i), \quad z_i = h_i

• 单位球 S

  单位球的点云数据采用 球坐标系 (\theta_i, \phi_i) 表示：

  • 角度 \theta_i（方位角）均匀分布在 [0, 2\pi]。
  • 角度 \phi_i（仰角）均匀分布在 [0, \pi]。

  然后，球坐标被转换为 笛卡尔坐标系 (x_i, y_i, z_i)：

  x_i = \sin(\phi_i) \cos(\theta_i), \quad y_i = \sin(\phi_i) \sin(\theta_i), \quad z_i = \cos(\phi_i)

这意味着：

• \theta_i 控制水平方向的旋转（围绕 z 轴旋转）。
• \phi_i 控制垂直方向的仰角，确保点云均匀分布在整个球体表面。

可视化代码：https://paste.org.cn/Untq9z8xFc