最近在看场的内容,看看这篇,这篇被Sig和Sig Asia拒稿,最后投在CGI2025
论文链接:https://link.springer.com/article/10.1007/s00371-025-04008-2
Abstract
在图形学中有一个高精度的多边形网格\mathcal{M},可能有很多的三角形,这非常耗时间和占内存,所以往往需要用一个更简单的几何代理(proxy)来代替,保证和原模型接近。ImS就是为这种情况设计的,并非显示存储表面模型,而是隐式地表示一个围绕原模型的薄壳区域。
ImS数学定义:
用一个函数f(x)来近似SDF,并定义了一个“壳层”
\{\mathbf{x}\in\mathbb{R}^3\mid \epsilon_1\leq f(\mathbf{x})\leq \epsilon_2,\epsilon_1 < 0, \epsilon_2>0\}\epsilon_1和\epsilon_2就是内外边界的SDF值\epsilon_2-\epsilon_1就是厚度- 目标让厚度尽量小,但仍然被
\mathcal{M}包裹住
为了兼顾数学简洁性和表达能力,他们用了一阶三变量张量积 B 样条(tensor-product B-spline) 来表示 f:
- 这样可以用光滑的曲面来近似 SDF。
- 还会自适应地调整 B 样条的 knot grid(节点网格),以适应不同部位的形状变化。
快速求解与稀疏线性系统
有了B样条之后,f的解析式可以直接写出来,为了计算,求解一个稀疏线性系统,可以快速求解。并且在寻找f的极值时候,不是遍历模型上无限点,而是从一组候选点中选取最值。
Introduction
为了缓解负担,提出了几何代理(Geometric Proxies),是一种简化但保留关键特征形状的代替表示。
Shell结构是一种特殊的几何表示形式,由内/外两层的偏移曲面组成。
生成壳的挑战:质量、精度和效率之间的矛盾(高精度计算慢、高效率精度差)
分类:
-
显式方法(Explicit)
复制原始表面并沿法线或距离函数偏移
缺点:在复杂形状或者高亏格表面上容易自交
-
隐式方法(Implicit)
用数学函数SDF、B-样条隐式描述壳
优点:能生成平滑、连续变化的壳厚
B-样条
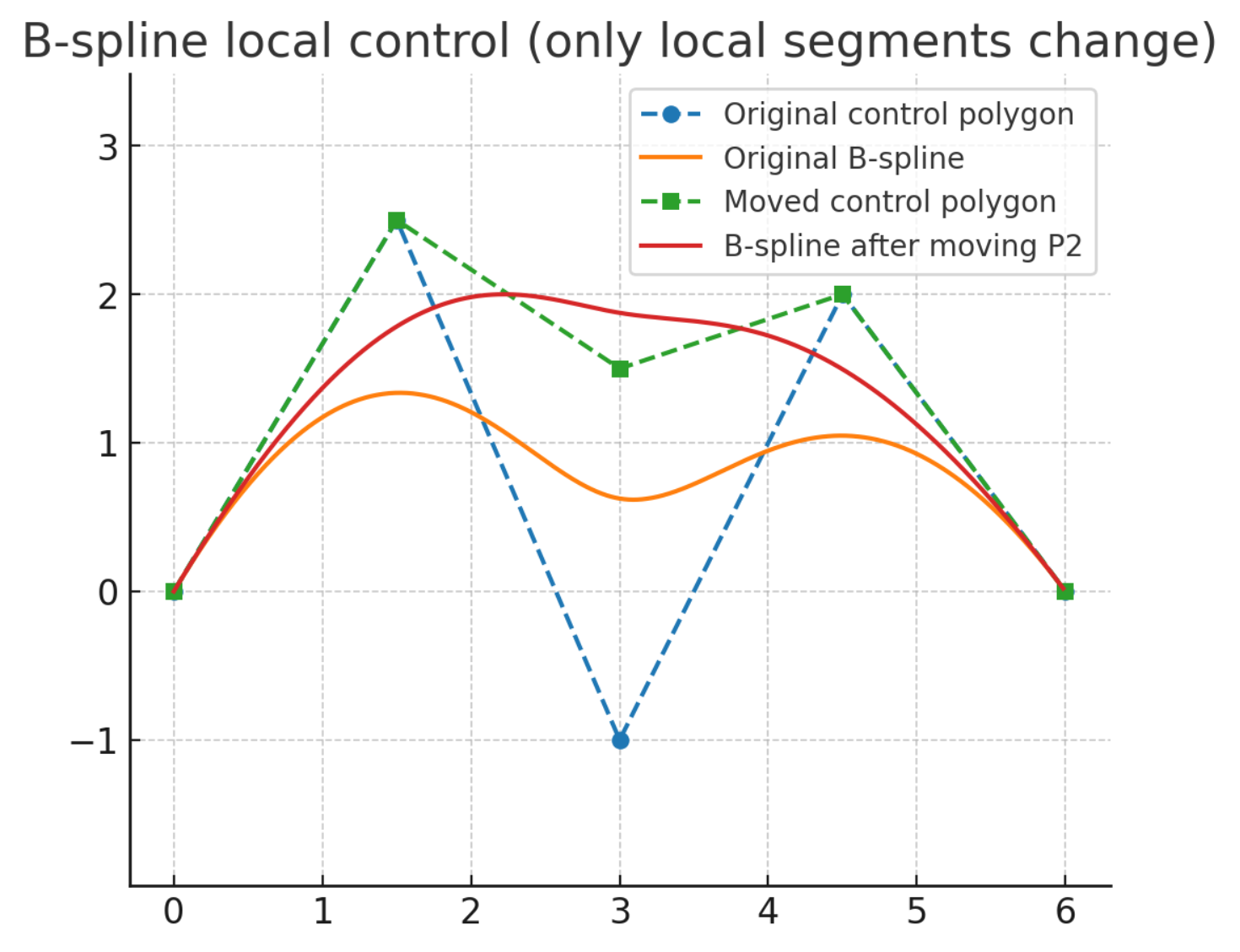
隐式方法和壳层Shell。隐式方法用一个函数(通常是距离场)和两个距离值来定义壳层的内边界和外边界,就像[\epsilon_1, \epsilon_2]表示壳层所表示的区域。
本文挑战是用一个函数f来表示sandwich-walled space(双面壳层空间),如果直接用SDF也是可以的但是SDF没有解析形式,计算不便。本文采用三变量张量积B样条来近似SDF,公式是:
\{v\in\mathcal{M}\mid f(v)\in[\epsilon_1,\epsilon_2]\}负表示在里面,正表示在外面,\epsilon_1<0,\epsilon_2>0
对f的要求是:
- Tightness:二者尽量接近,壳层要薄
- Rigorousness:保证
\epsilon_1\leq f(\mathcal{M})\leq \epsilon_2,完全包住网格 - Expressiveness:复杂几何形状也可以找到合适的
f - Rapid retrieval:能快速计算出
f的值,计算代价低
ImS可以直接把壳层当作计算区域进行操作,也可以作为Proxy(代理)加速点和表面的距离、包含性判断
技术路线:
本文使用的是一阶B样条,把多边形网格的SDF转换成B样条表达式,寻找f的极值的时候,不再无限多点中寻找,而是有限候选点中找,并且用稀疏体素八叉树(SVO)而不是均匀八叉树
💡贡献
- 提出用三变量张量积 B 样条表示输入表面的双面壳层空间的新方法。
- 提出有限候选点搜索的极值求法,严格包裹网格。
- 将 ImS 与 QEM(Quadric Error Metrics)结合,实现带全局误差控制的网格简化。
Related works
本文更多关注于生成壳层的隐式曲面重建和显示的边界笼创建
隐式表示
隐式表面重建的问题是给定一个点云,拟合出一个由函数定义的水平集曲面。
通常用函数表示为已建立的基函数的线性组合,包括:
- B样条基函数
- 径向基函数RBF
- 小波(Wavelets)
- 傅里叶基
显示生成边界笼
Bounding cages作为多边形网格的边界代理,充当壳层的简化外部边界
Method
SDF表面\mathcal{M}想得到一个f:\mathbb{R}^3\rightarrow \mathbb{R}
f(v)\approx 0,\quad \forall v\in\mathcal{M}用tightness公式来量化\epsilon_1和\epsilon_2接近程度
E(f)=\max_{v\in\mathcal{M}}f(v)-\min_{v\in\mathcal{M}}f(v)将 f 限制为三元张量积 一阶 B 样条基函数 的形式,这样能减少计算复杂度并方便找到极值。
这里开始讲隐式化部分,即Implicitication。
我一直对这里有一个疑问,这里为什么叫隐式化?明明B样条基函数这类都是显式的式子。首先我们输入是Mesh这类的网格,然后用SDF来表示,平时大家的SDF有人用神经网络来训练
f,但是这里用的是B样条基函数来拟合f。隐式/显式是看你表示几何的方式,而不是看你用的数学工具是不是显式公式。
目标:用tensor-product B-spline来显示表示f,而f近似隐式地编码SDF。
优势在于能将空间划分成规则网格(grid cells),局部定义基函数,为了满足快速查询,这里要求是一阶(first-degree)的。
B-spline定义
一维一阶B-spline:
B(t)=\left\{\begin{array}{l l}{1+t,}&{t\in[-1,0]}\\ {1-t,}&{t\in(0,1]}\\ {0,}&{\mathrm{otherwise}}\end{array}\right.三维情形通过张量积得到:
B(\mathbf{v})=B(x)B(y)B(z)这里\mathbf{v}=(x,y,z)^\mathrm{T}。如果网络边长为w,则以网格点g为中心的基函数为:
B_{g}(\mathbf{v})=B\left(\frac{\mathbf{v}-\mathbf{g}}{w}\right)最后所有由基函数生成的函数可以写为:
f(\mathbf{v})=\sum_{\mathbf{g}\in\mathcal{G}}\lambda_{g}B_{g}(\mathbf{v})其中\mathcal{G}是所有网格点,\lambda_g是带求的系数。
稀疏体素八叉树(SVO)
文章还使用了稀疏体素八叉树(SVO),之前只了解过八叉树,其实在我看完这篇论文之后加了解一些之后也有了清楚的认识了。
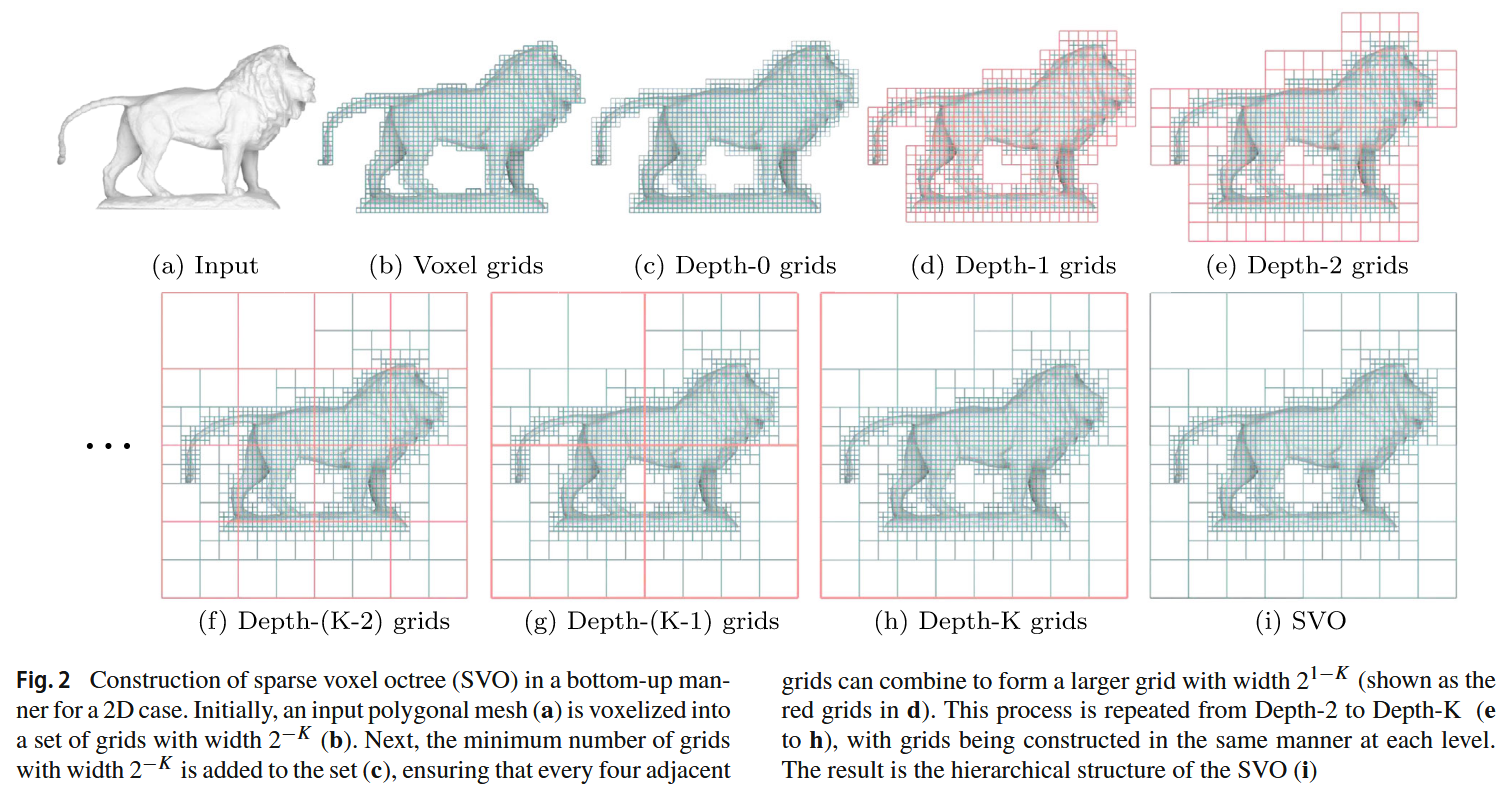
总结:只在多边形网格表面附近体素化(voxelization),减少不必要区域的网格(如上图)
有以下的思考:
1.查找 我们的目的就是为了用B-样条来拟合f函数即SDF场,现在查询一个点\mathbf{v}=(x,y,z)只需要找它最近的八个格点(grid point)来计算,通过那八个基函数来计算通过距离来分配权重,权重公式的本质就是三线性插值:
w_g=(1-|x-g_x|/w)(1-|y-g_y|/w)(1-|z-g_z|/w)2.SVO 八叉树其实就是算法竞赛中线段树的三维体现,比如一个结点维护的就是这个\mathbb{R}^3空间上的信息,例如在某一个区域有多少个点云的点,这可以在\log级别进行计算出来。那么SVO稀疏体素八叉树呢?就上图一样,不需要的地方就不往下递归了,有点像线段树里面的lazytag。那么此时对于一个点附近八个格点也许就不是正方体了,而可能是一个不规则的图形了。
3.维护? 那么这个SVO稀疏体素八叉树维护了什么信息吗?其实没有,就是在快速找到某个点附近的格点信息。
4.结点重复 在B样条情况下,每个基函数是以格点为中心,支撑范围取决于当前深度cell的尺寸,如果在深度k有一个角点坐标是(2,2,2),它这确实有一个基函数B_{g,w_k},支撑范围大,但在k+1深度的时候也可能有一个(2,2,2)的角点,这时候对应的基函数B_{g,{w_{k+1}}} ,但这个时候支撑范围小了。文中也提到了
两个位置相同但深度不同的点被认为是不同的格点
(it is worth noting that two points at the same position but with different depths are considered distinct)。
5.重复角点计算? 比如对于点(1.2,3.7,0.4)找到了(2,4,1)这个角点,但是对于它来说有很多深度的对应的基函数,都应该累加,而不是使用单一层。所以每层最多8个权重。都用各自尺度w_k,w_{k+1}和系数\lambda_{g,k},\lambda_{g,k+1},最后累加成为f(\mathbf{v}),即
f(\mathbf{v})=\sum_{k=0}^{K}\sum_{\mathbf{g}\in\mathcal{G}^{k}}\lambda_{\mathbf{g}}B\bigg(\frac{\mathbf{v}-\mathbf{g}}{w_{k}}\bigg)所以我们需要求解\lambda_g 来确定f。我们将网格点g\in \bigcup_k\mathcal{G}^k都代入如下公式(8)中
f(g)=D(g,\mathcal{M}),\quad\forall g\in\bigcup_{k}\mathcal{G}^{k}右端的D用Fast Winding Number来计算“符号”,再配合网络的最近距离得到带符号距离。把v=g代入展开式,得到关于系数\lambda的线性方程,对所有的g都进行,得到了一个稀疏、对称但不一定正定的线性系统A\lambda =b。通过最小二乘共轭梯度(LSCG,Eigen)来求解。
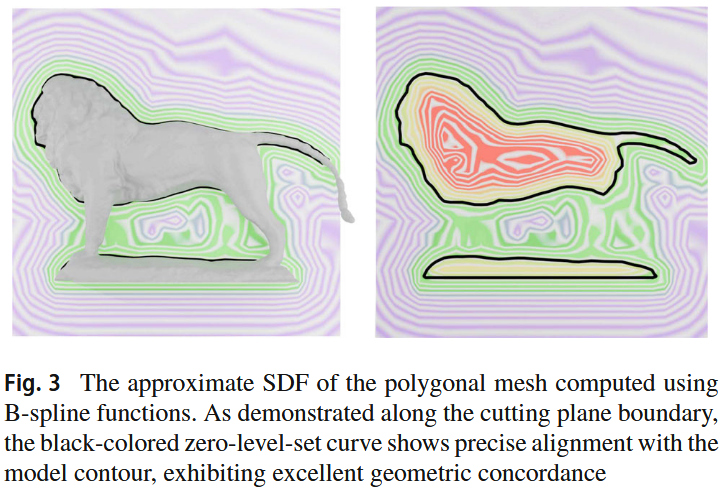
总而言之,我们格点到表面的距离我们可以通过D(g,\mathcal{M})通过很成熟的算法来得到,也就是计算距离(到mesh)和计算符号(FWN),那么未知数就只有λ了。伪代码
build BVH for triangles of M
build FWN hierarchy for M
for each grid point g in ⋃k G^k:
# 最近距离
(p*, T*) = nearest_point_on_mesh(g, BVH) # 返回最邻近点 p*
d = norm(g - p*)
# 符号:Fast Winding Number
W = fast_winding_number(g, FWN)
s = +1 if W > 0.5 else -1
# 可选:若 |W-0.5| < tau,用 (g-p*)·n_T* 的符号做精判
if abs(W-0.5) < tau:
s = sign( dot(g - p*, normal_of(T*)) )
D[g] = s * d如何精确地找到包裹整个模型的隐式外壳(Implicit Shell)的边界
从而得到论文里说的“壳层”范围\epsilon_1\leq f(\mathcal{M})\leq \epsilon_2
极值点首先需要选一个候选集C_T
在三角形T中(它完全在 Depth-0 的一个格子(grid cell)内),三角形内任意一点都可以用重心坐标来表示
v=(v_{2}-v_{1})\alpha+(v_{3}-v_{1})\beta+v_{1},\quad0\le\alpha,\beta,\alpha+\beta\le1这样把原来的f(v)转换为H_T(\alpha, \beta),然后
- 梯度为.
\nabla _{\alpha,\beta}H_T=0可以得到部分极值候选点。 - 边界上的极值。就是一维函数
\hat{H}_T(t),也就是\alpha=0,\beta=0,\alpha+\beta=1时候,求导为的候选点。 - 三角顶点
并且限定\epsilon_1,\epsilon_2的范围,
\epsilon_{1}=\operatorname*{min}_{v\in C}f(v),\quad\epsilon_{2}=\operatorname*{max}_{v\in C}f(v)满足
\epsilon_{1}\le f(\mathcal{M})\le\epsilon_{2}的空间就是包裹网络表面的“壳层”
为什么只在 Depth-0 cell 内找极值?
因为 Depth-0 是最粗的网格,它们会包含三角形,但每个三角形都被限制在一个 cell 内,所以极值搜索范围就有限,减少计算复杂度。
定理1指出,我们只需要在这个有限的集合 C 中寻找函数 f 的最大值和最小值,就能得到整个模型表面的最大值 ε₂ 和最小值 ε₁ 。这样做可以
我不禁有一个疑问:这里在干什么?简而言之:求这个壳层,求表面上f的上下界
表面上的点很多,但是我们可以通过有限点来快速求出来。
B-spline 是平滑的,所以 f 在三角形内可能有一个局部极小值或极大值,这些值有可能出现在顶点、边界上、或内部某个位置。
有了壳层之后,在后面的碰撞检测或者可见性分析里面就只需要再一个小范围搜索,而不是全空间。
可能会先想:
一个三角形的顶点 f 值确定了,中间插值,不就是个平面吗?那怎么会有内部极值?
这是对线性插值成立的,但这里 f 是通过B-spline 基函数的加权和得到的,而 B-spline 基函数是平滑曲面,不是线性平面。
所以在一个三角形内部,f 的形状是三维“弯曲”的曲面:
- 它可能向上凸(像个小山包),那么三角形内就有一个局部最大值。
- 它可能向下凹(像个小坑),那么三角形内就有一个局部最小值。
所以!一个三角面片用B-spline基函数叠加出来拟合会称为一个光滑曲面,在这个曲面上值肯定是不一的,所以我们需要一个球壳来定义这个表面完全包裹住。
那为什么不直接拟合成直面呢?这是因为B-spline有平滑优势。是一种权衡,偏差足够小表示精度也很高了!
Limitation
(From GPT)
表达能力 vs. 复杂细节
他们用的是一阶B-样条(分片三线性),精度完全靠 SVO 的深度 𝐾扛;薄结构、强曲率、狭缝等就必须把𝐾拉很高,代价是内存与时间快速上升(作者也在“Limitations”里承认了)。这类区域会出现“锯齿/台阶”→再靠 SVO 细化去抹平。
线性系统可能奇异/非唯一由于子基函数能重构父基函数,矩阵稀疏对称但非正定,会出现奇异/非唯一解,只能用最小二乘共轭梯度给个可行解;这对“极值严格性”的理论边界其实比较脆弱(数值上要靠阈值与取整修正)。
SDF 近似依赖“点到面距离”的外部黑箱右端D(g,M) 全仰赖 Fast Winding Number(FWN),FWN 在离面很近时会有数值敏感;作者也在性能节里承认“极少数点非常靠近表面时”分类会出错。
“候选极值点”的完备性依赖于三角形完全落在 Depth-0 单元相交时需要细分成子三角形,否则极值检查并不完备;实现层面会引入额外切分与边界条件分支。
