Deformable Radial Kernel Splatting & Scaffold-GS: Structured 3D Gaussians for View-Adaptive Rendering
Abstract
传统高斯是径向对称和平滑的,DRK(可变性径向核)可以进行学习,更加灵活、通用。可以更好地拟合不同性质的原语(边、角、曲线等),并且能精细控制边缘的清晰度与边界曲率
DRK的核具有平面特性,它们不一定3D对称而可以近似为扁平或2D形态的核,用少数核来表示,而3DGS需要用很多
1.Introduction
三个核心设计:
- 不再是一个“圆形”的高斯,而是多个径向分布的极坐标基组合
- 混合距离度量L1+L2,使得DRK在表达平滑表面和锐利边缘时都更加自然
- 分段线性重映射函数
2.Related Work
3D高斯核的挑战就是它是光滑对称的,对于锐边以及复杂几何结构的时候,表达能力不够,常常通过堆很多的高斯去逼近
这里需要设计新的kernel类型(非高斯、非球对称)
3.Preliminaries
每个高斯\mathcal{G}包含以下成分:
G_j=\{\mu_j,q_j,s_j,o_j,sh_j\}
\mu_j:中心位置q_j:旋转四元数,控制高斯的方向(旋转)s_j:缩放因子,控制高斯大小o_j:不透明度sh_j:球谐函数,控制颜色随视角的变化
📐 类比总结:
| 表示方式 | 从正面看 | 从侧面看 | 表达复杂结构 | 渲染稳定性 |
|---|---|---|---|---|
| 3DGS(椭球体积) | ✅ 清晰 | ✅ 仍可见 | 中等,需要堆叠 | 稳定但冗余 |
| 2DGS(贴纸) | ✅ 清晰 | ⚠️ 可能不可见 | 一定能力 | 不稳定(视角敏感) |
| DRK(智能贴纸) | ✅ 清晰 | ✅ 更稳健 | 高,可自适应形变 | 稳定又紧凑 ✅ |
我感觉2DGS很像纹理,也有其中的
u,v坐标,获取之后再去查询核函数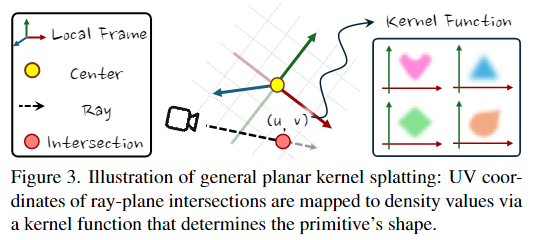
4. Deformable Radial Kernel Splatting
DRK是用一组可学习的径向基函数定义出一个在平面上的“可变形核形状”。参数集合如下:
\Theta = \{\mu,q,s_k,\theta_k,\eta,\tau,o,sh\}
| 参数 | 含义 | 说明 |
|---|---|---|
\mu \in \mathbb{R}^3 |
位置 | 原语中心点(空间坐标) |
q \in SO(3) |
方向 | 控制切平面的朝向(通过旋转矩阵) |
s_k, \theta_k |
径向基参数 | 控制核的每一条“射线”:长度和角度,共 KKK 条,决定核的轮廓形状 |
\eta \in (0,1) |
曲率 | 控制轮廓曲线是圆滑的还是接近直线 |
\tau \in (-1,1) |
锐度 | 控制边缘是软边模糊还是锐利 |
o |
不透明度 | 控制这个核整体的“强度” |
sh |
球谐系数 | 控制随视角变化的颜色外观(像反光、金属感等) |
🎯创新点
- 用径向基定义形状,将核的形状建模从中心向四周发射K条方向的向量,每条都有一个长度
s_k和方向\theta_k,这样核函数的形状不再是圆或者椭圆 - 引入曲率和锐度参数(
\eta,\tau)
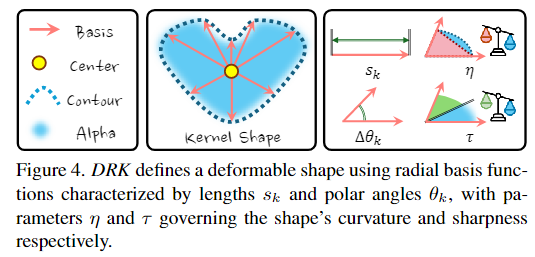
4.1 Radial Basis(径向基)
核的形状看作是由K个方向射线组成的极坐标轮廓,每条射线有方向角\theta_k和射程长度s_k
任何一个点(u,v)都可以转换成极坐标
- 半径:
r_2=\sqrt{u^2+v^2} - 角度:
\theta=\arccos (u/r_2)
然后可以找出\theta落在哪两个控制点之间,比如\theta_k\leq\theta\leq \theta_{k+1}进行插值
插值公式是一个余弦加权的插值
4.2 L1&L2 Norm Blending(混合范数)
只用L2范数会导致核边缘是圆形或者弯曲的,无法拟合直线边界
所以引入L1,在(x+y=1)等方向上形成菱形结构,更好表现直边
加权组合
4.3 Edge Sharpening(边缘锐化)
高斯分布的边缘总是渐变模糊的,既是很小的标准差也很难表现锐利的边界
引入Sharpening Function函数,参数是\tau\in(-1,1)
Scaffold-GS: Structured 3D Gaussians for View-Adaptive Rendering
Abstract
同样是与3DGS比较,这里展示了创新点主要在于
Scaffold-GS=结构化高斯建模 + 按需动态推理
核心的有:
- Anchor Points(锚点):少量“锚点”来表示场景结构,作为高斯的中心依据
- 局部高斯分布:每个锚点可以在其局部区域内生成多个高斯
还有其他就是CV视角等方面了,动态推理每个高斯的大小、形状、透明度等属性
也可以自动裁剪不需要的锚点(压缩表示)
可以把Scaffold-GS看作:
从点云 → 到结构驱动表示 → 再到视角动态推理的一步
更关注结构组织性(scaffold)和渲染适应性(adaptive),而DRK更像是在单个原语层面做了极致的表达优化
3. Methods
从SfM得到的稀疏点云构建anchor points,然后从每一个anchor出发,动态生成一组neural Gaussians用来适应当前的视角
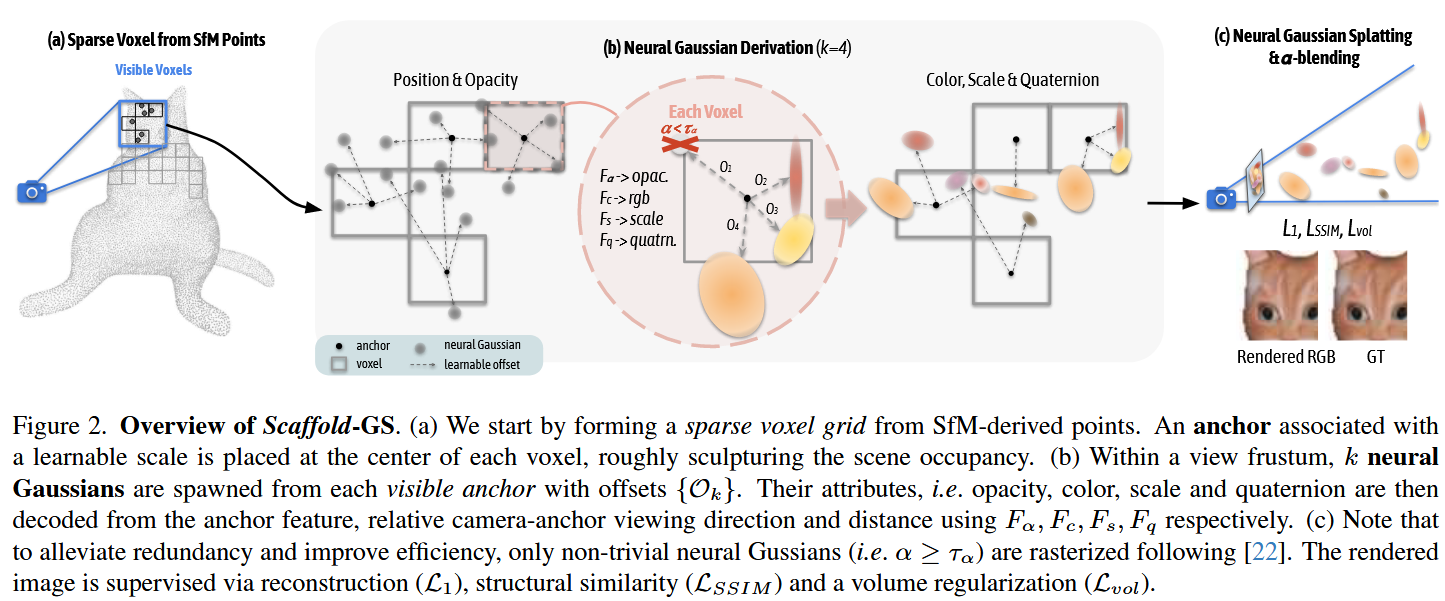
根据图二来看,进行拆解
📍第一步:建立稀疏锚点结构(anchor scaffold)
- 输入是SfM重建得到的点云,Scaffold-GS将其voxelize(体素化)为规则网格,每个体素中心生成一个anchor point,每一个anchor有一个可以学习的特征和位置(+方向、尺度等初始值)
📍第二步:从anchor动态派生出多个高斯。
- 每个可见anchor在当前视锥体内会派生出多个k个高斯核,每个高斯具有anchor的偏移位置,属性包括
F_a:透明度、F_c:颜色、F_s:尺度、F_q:方向(四元数) - 这些高斯属性不是直接学习的,而是从anchor feature经过网络推理得到的
📍第三步:α-blending渲染
- 同3DGS,还是采用高斯投影+α混合。投影之后变为2D高斯斑点,根据透明度之后进行排序blending
✅ Scaffold-GS 与 3DGS 的根本区别:
| 方面 | 3DGS | Scaffold-GS |
|---|---|---|
| 原语数量 | 固定,每个点对应一个高斯 | 动态生成,每帧按需生成 |
| 原语属性 | 每个高斯独立学习 | 从 anchor 中推理出 |
| 几何感知 | 弱,点→高斯直接转换 | 强,anchor 结构表达全局几何感 |
| 表示稀疏性 | 差(需要大量高斯堆) | 优(高效表达局部结构) |
| 渲染视角适应性 | 固定 | ✅ 可根据视角和距离动态调整 |
总结:
Scaffold-GS 用一个 结构化的 anchor 网格作为“框架”,通过动态推理生成高斯原语,在保持渲染效率的同时,大大提升了表示能力和稀疏性。
3.2. Scaffold-GS
3.2.1 Anchor Point Initialization
这里讲述如何初始化,从稀疏点云构建锚点,并生成高斯分布特征的
voxelization:
\mathbf{V}=\{\left \lfloor \frac{\mathbf{P}}{\epsilon} \cdot \epsilon\right \rfloor \}
这样从M个点得到了N个体素中心
每个锚点v都有一些属性
| 参数 | 类型 | 解释 |
|---|---|---|
f_v \in \mathbb{R}^{32} |
特征向量 | 表示 anchor 的局部上下文 |
l_v \in \mathbb{R}^3 |
缩放因子 | 控制 anchor 支配范围 |
\mathcal{O}_v \in \mathbb{R}^{k \times 3} |
learnable offsets | 用于生成该 anchor 下的多个高斯原语 |
多尺度特征bank:对于每一个锚点v都有原始特征f_v,f_{v↓1},f_{v↓2},这里的↓n表示下采样(down-sampled),通道数减半、再减半
视角自适应融合:通过摄像机和锚点的位置可以计算距离\delta_{vc}和方向\vec{d_{vc}},进入到小MLPF_w中得到三个softmax权重,
\{w,w_1,w_2\}=\mathrm{Softmax}(F_w(\delta_{vc},\vec{d_{vc}}))
用于加权三种分辨率的特征
\hat{f_v}=w\cdot f_v+w_1\cdot f_{v↓1}+w_2\cdot f_{v↓2}
最终获得一个与视角有关的anchor特征\hat{f_v}
📌 这样得到的 anchor 特征 \hat{f}_v 会随着视角自动变化,形成视角自适应分布结构
3.2.2 Neural Gaussian Derivation
这里揭示了一个anchor点是怎么实际生成多个neural Gaussian的?
还是与3DGS的高斯核一样包含以下属性:\mu,\alpha,q,s,c分别是位置、不透明度、四元数(控制旋转方向)、缩放因子、RGB颜色
对于每个可见的anchor x_v,生成k个neural Gaussians
\{\mu_0,...,\mu_{k-1}\}=\mathbf{x}_v+\{O_0,...,O_{k-1}\}\cdot l_v\tag{8}
O_i\in\mathbb{R}^3:是可学习的偏移向量,每个anchor自带k个l_v\in\mathbb{R}^3:是anchor的局部缩放比例(初始化学习到)
这样可以控制这些高斯在局部空间中生成
其他的视角相关的特征就在MLP中推理,以不透明度\alpha为例
\{\alpha_0,...,\alpha_{k-1}\}=F_\alpha(\hat{f_v},\delta_{vc},\vec{\mathbf{d}}_{cv})
这意味着每一帧都是动态生成的
Scaffold-GS 不像 3DGS 那样一开始就创建几十万个高斯,而是:当前相机看得见哪些 anchor,就只从它们生成高斯
“...only keep neural Gaussians whose opacity values are larger than a predefined threshold
\tau_\alpha.”某些生成的高斯很透明,就直接丢弃,设置了一个阈值
3.3 Anchor Points Refinement(锚点优化)
这里讲述了锚点的优化,原始的anchor是从SfM得来的,是稀疏不均匀的,这里要做两件事情:
- Growing(生长):往重要但缺失的地方加anchor
- Pruning(剪枝):把没用的anchor移除
因为方向的原因,我这里大致写点了
这里涉及到多分辨率,小网格看细节,大网格看粗糙区域。
统计每个体素中的neural Gaussians的梯度大小\nabla_g(越重要的区域梯度变化越大,对voxel计算平均梯度)如果平均梯度超过阈值那么就说明重要
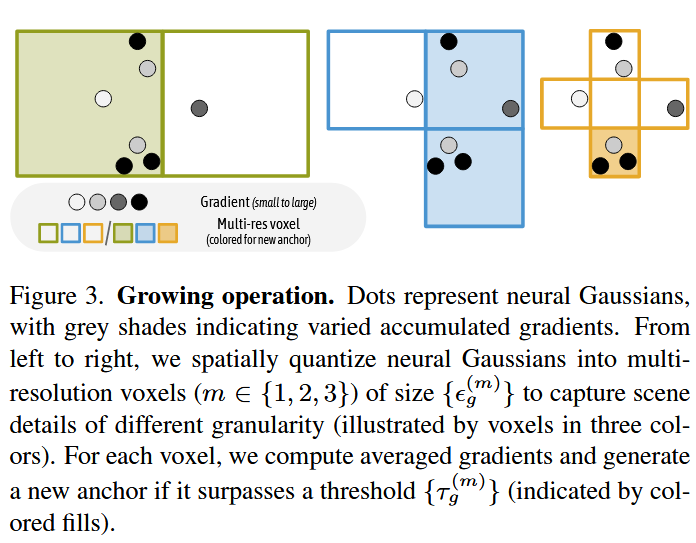
图三中的灰色点表示已有的高斯,灰度深浅表示梯度的强弱,彩色框表示anchor所在的位置(阈值超过)
Pruning Operation :删除无用的anchor
训练中不断生成neural Gaussians,记录它们的\alpha透明度累计值,如果某一个anchor总是很透明那么可以删
