卷绕数与广义卷绕数

这一篇谈谈我对卷绕数（Winding Number）以及广义卷绕数（Generalized Winding Number）的理解，以下或许会简称为WN和GWN。我现在主要是做点云方面的，所以我这是点云相关的，仅供参考

由于工作主要需要用到广义卷绕数，这里会写的比较详细

一、卷绕数

1.1 卷绕数介绍

第一次接触到卷绕数是在KNN Crane上的离散微分几何（DDG）课上，那时候介绍了许多公式，例如与亏格一起计算等。这里放一下维基百科的🔗卷绕数 - Wiki

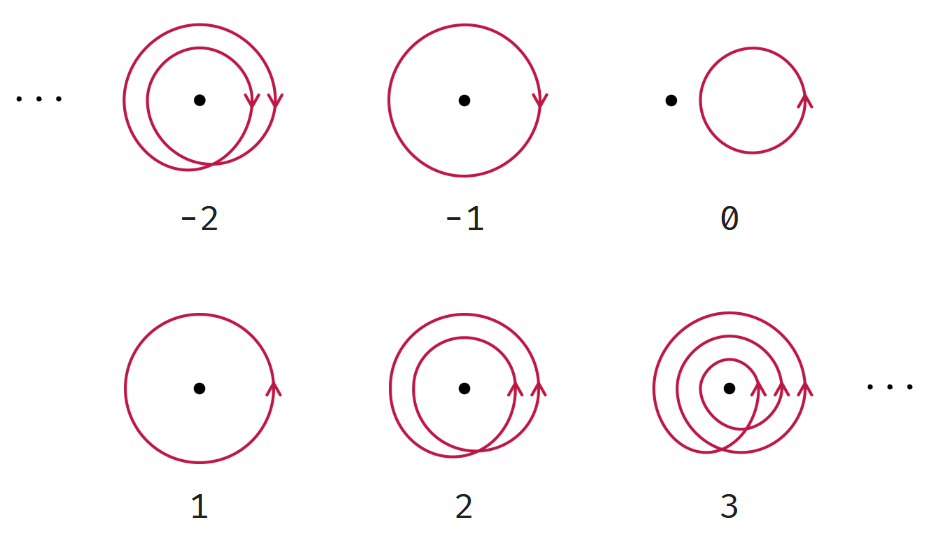
卷绕数表示在二维平面内一个曲线环绕一个点多少次，正式地说，曲线的卷绕数就是物体逆时针绕过原点的总次数。需要注意两点：

• 卷绕数可以使任何整数
• 逆时针方向为正

在点云中我们可以将上面的曲线用离散的点云来表示，在二维中我们就考虑某点被点云环绕了多少次（不考虑方向）；在三维中也是一样的，也就是曲线变曲面的一个过程。一般点云只会是空心的（不一定全包围，也可能是开表面）

【开表面】例如喝水的马克杯，没有杯盖可以让其封闭，那么此时我有两种思考：

1. 使用一种方法让其进行封闭，例如给它盖上盖子，这是一种挑战
2. 或者让卷绕数并不局限于整数，可以是0.75等数，BIM可以做到

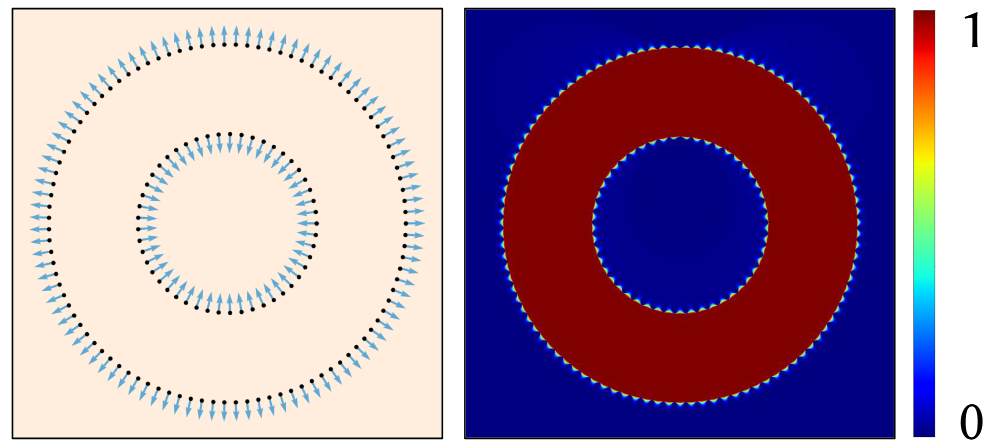
以上图二维点云中两个圆圈为例，圆环里面被两个大小圆圈进行包裹，那么里面的任何一个点都被环绕了一圈，所以值为1，其余为

1.2 卷绕数计算公式

W(p)=\dfrac{1}{4\pi}\iint _S\dfrac{\vec{r}\cdot \hat{n}}{r^3}\mathrm{ds}

• S=\part \Omega为曲面
• \vec{r}是从p指向曲面微元的向量
• \hat{n}是\mathrm{ds}的单位法向量

我们有以下几个步骤

1️⃣Step 1: 表面重建

可以看到这里需要用到曲面微元，所以我们需要一个表面才可以获得Winding Number。

可以用到：

• 泊松表面重建（PSR）
• Marching Cube（🔗Marching Cube算法 - CarryNotKarry）
• ...

2️⃣计算绕数（Winding Number）积分

1. for triangles计算点p的立体角贡献\Omega_i
2. 求和\sum \Omega_i
3. 归一化得到W(p)=\dfrac{1}{4\pi}\sum \Omega_i

3️⃣立体角计算公式

\tan\frac{\Omega}{2}
=
\frac{\vec a\cdot(\vec b\times\vec c)}
{\|\vec a\|\,\|\vec b\|\,\|\vec c\|
\;+\;(\vec a\cdot\vec b)\,\|\vec c\|
\;+\;(\vec b\cdot\vec c)\,\|\vec a\|
\;+\;(\vec c\cdot\vec a)\,\|\vec b\|}

• 注意这里的符号，\tan\frac{\Omega}{2}是三重标量积；还有点积和模长（长度）

\Omega
=
2\arctan\!\biggl(
\frac{\vec a\cdot(\vec b\times\vec c)}
{\|\vec a\|\,\|\vec b\|\,\|\vec c\|
\;+\;(\vec a\cdot\vec b)\,\|\vec c\|
\;+\;(\vec b\cdot\vec c)\,\|\vec a\|
\;+\;(\vec c\cdot\vec a)\,\|\vec b\|}
\biggr)

这样就可以求得\Omega了

💡直观感受：

卷绕数反映曲面对查询点q的“包裹程度”（后面会详细解释）

• 内部点：总立体角贡献为4\pi（完整球面），所以要归一化除以4\pi
• 外部点：贡献为

二、广义卷绕数

2.1 广义卷绕数计算公式

w(\mathbf{q})
\;=\;
\frac{1}{4\pi}\,\oint_{S}\mathrm{d}\Omega
\;=\;
\oint_{S}
\frac{\langle \mathbf{x}-\mathbf{q},\,\mathbf{n}_x\rangle}
{4\pi\,\|\mathbf{x}-\mathbf{q}\|^3}\,\mathrm{d}x

• \mathbf{n}_x表示在点x处的法线
• q是查询点，x是积分的单元

那么问题来了，与非广义的卷绕数有何不同？

重点就是在这法线上，这里进一步将法向量\mathbf{n}_x作为变量引入。

其实很容易思考，我们在做表面重建的任务的时候，我的目的就是为了通过卷绕数求得表面，那么按照之前所说的卷绕数求解方法还需要构建表面求解，岂不是倒反天罡了吗？

所以我们使用广义卷绕数来求解法线，通过求解法向一致的\mathbf{n}得到我们最后的结果。

那么我们可以通过广义卷绕数（GWN）来看，对于任意点q，GWN是曲面曲面S上所有x对q的贡献之和，贡献由

• 法向量\mathbf{n}_x
• 位置\mathbf{x}

决定。

2.2 理解卷绕数公式

我在这里通过广义卷绕数GWN来理解一下卷绕数公式，但是并不完全能解释，只有自己的略正确的理解，直觉上的推导过程。

1️⃣我们首先来看点云外部也就是卷绕数为的情况。

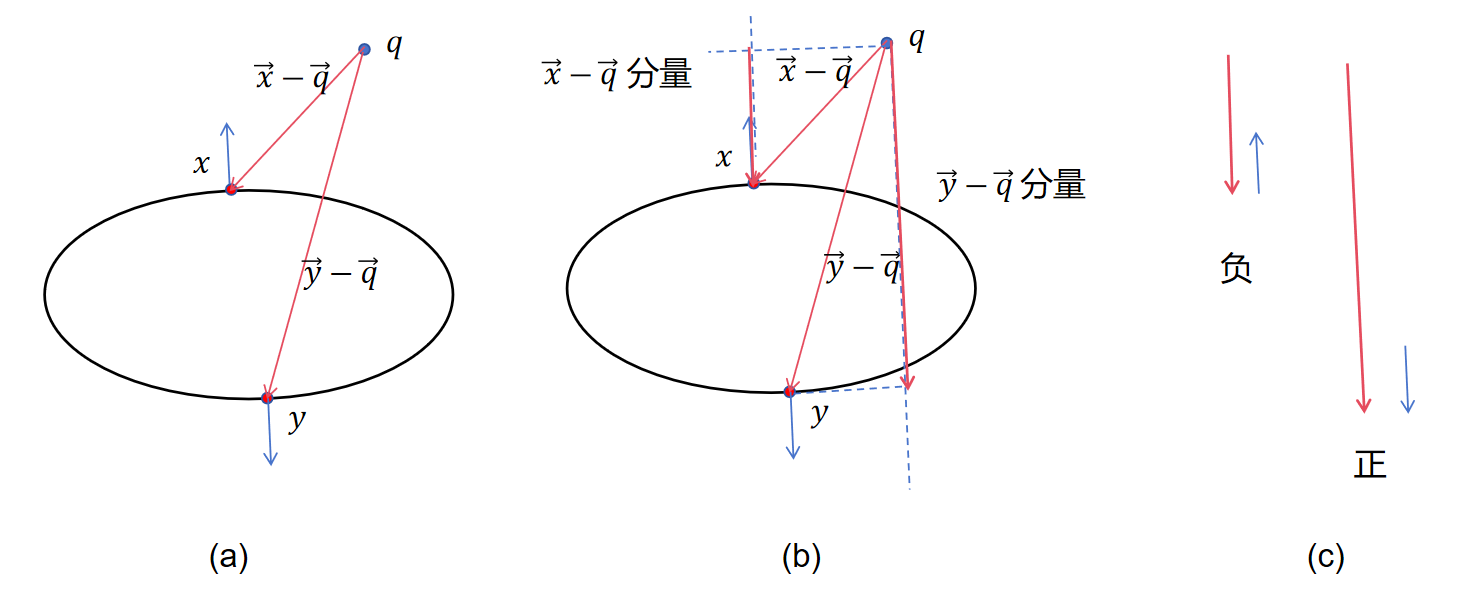
我们首先研究分子在干什么，分子为\langle \mathbf{x}-\mathbf{q},\,\mathbf{n}_x\rangle，一共分为三个部分

• 向量\mathbf{x}-\mathbf{q}
• 法线向量\mathbf{n}_x
• 点乘\langle \cdot ,\cdot \rangle

首先来看图(a)，把向量\vec{x}-\vec{q}画出来，注意是由q指向x，那么此时要与n_x进行点乘也就是要乘以一个角度\theta（未画出），我们可以对其做投影（分解）得到分量（图(b)），然后二者同方向直接相乘即可，我们可以从图(c)看出此时是一正一负。

直观来说，二者是不是可以抵消？但是长度不一样怎么办？

这就是说到分母，分母暂且不管4\pi，\|\mathbf{x}-\mathbf{q}\|^3可以使其进行一个归一化之后进行衰减

至于这里为什么是3，我并没有仔细研究数学推导，但我直觉认为的和GPT给我的相同，就是一个是由于归一化，另一个是由于积分，仅供参考

1. 投影关系给出一个 1/r^2 项

   从点 q 看向无穷远，曲面上一小块面积 dS 在视锥中投影到单位球面上的面积是

   d\Omega \;=\;\frac{\cos\theta\,dS}{r^2},\quad
   r=\|x-q\|,\quad
   \cos\theta=\frac{\langle x-q,\;n_x\rangle}{r}.

这里的 1/r^2 来自面积衰减（越远看越小）。

2. 点乘 \langle x-q,\,n_x\rangle 又带来一个 r 因子

   \cos\theta \;=\;\frac{\langle x-q,\;n_x\rangle}{\|x-q\|}
   \;=\;\frac{\langle x-q,\;n_x\rangle}{r}.

于是整体被积函数就变成

   d\Omega
   =\frac{\langle x-q,\;n_x\rangle}{r}\,\frac{dS}{r^2}
   =\frac{\langle x-q,\;n_x\rangle}{r^3}\,dS.

把这些合在一起，立体角积分就是

   w(q)
   =\frac{1}{4\pi}\!\smallint_{S}d\Omega
   =\frac{1}{4\pi}\!\smallint_{S}\frac{\langle x-q,\;n_x\rangle}{\|x-q\|^3}\,dS.

所以：

• 一个 r^2：来自面积投影到球面时的面积衰减；
• 另一个 r：来自点乘中把 \cos\theta 写成内积除以 r。

2️⃣那么我们再来看查询点在内部的时候，如图

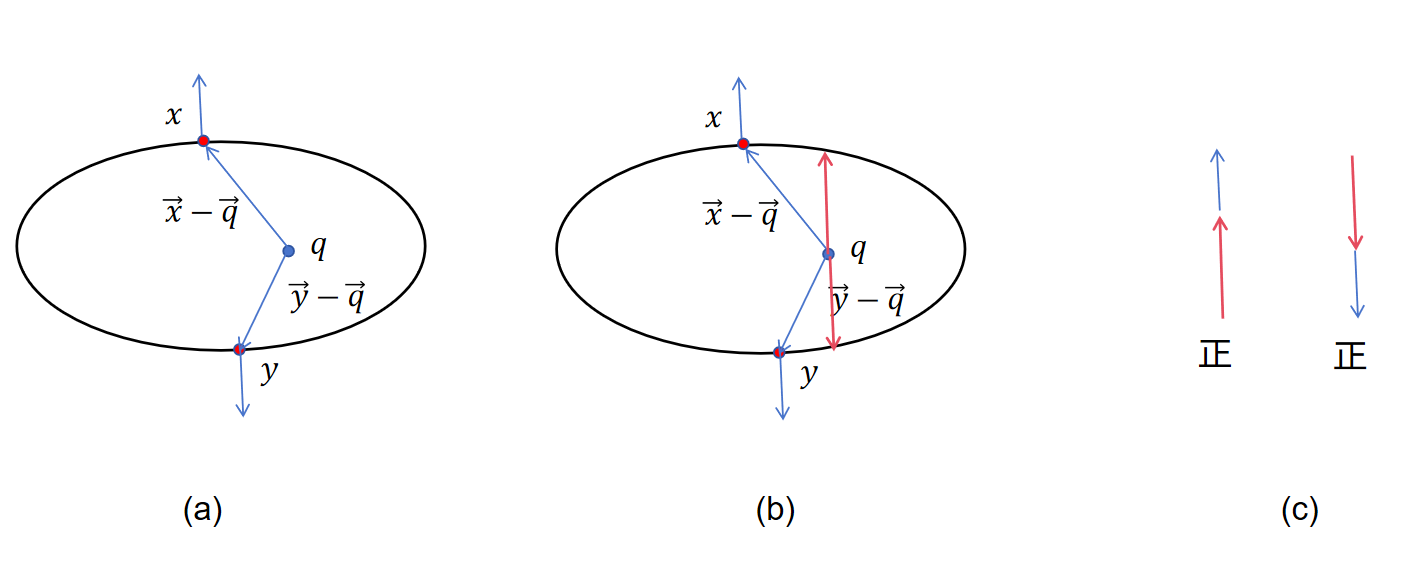
与之前类似，这样都是正的，也就是对于曲面上任意一个x进行积分都得到正数，最后积分结果应该是归一化球后表面积4\pi，所以要除以4\pi归一化成1

至此，公式所有都解释完毕

三、用途

接下来请转到DWG这篇文章🔗