样条

来源于B站视频：为什么要使用样条曲线？ - 奇点迫近

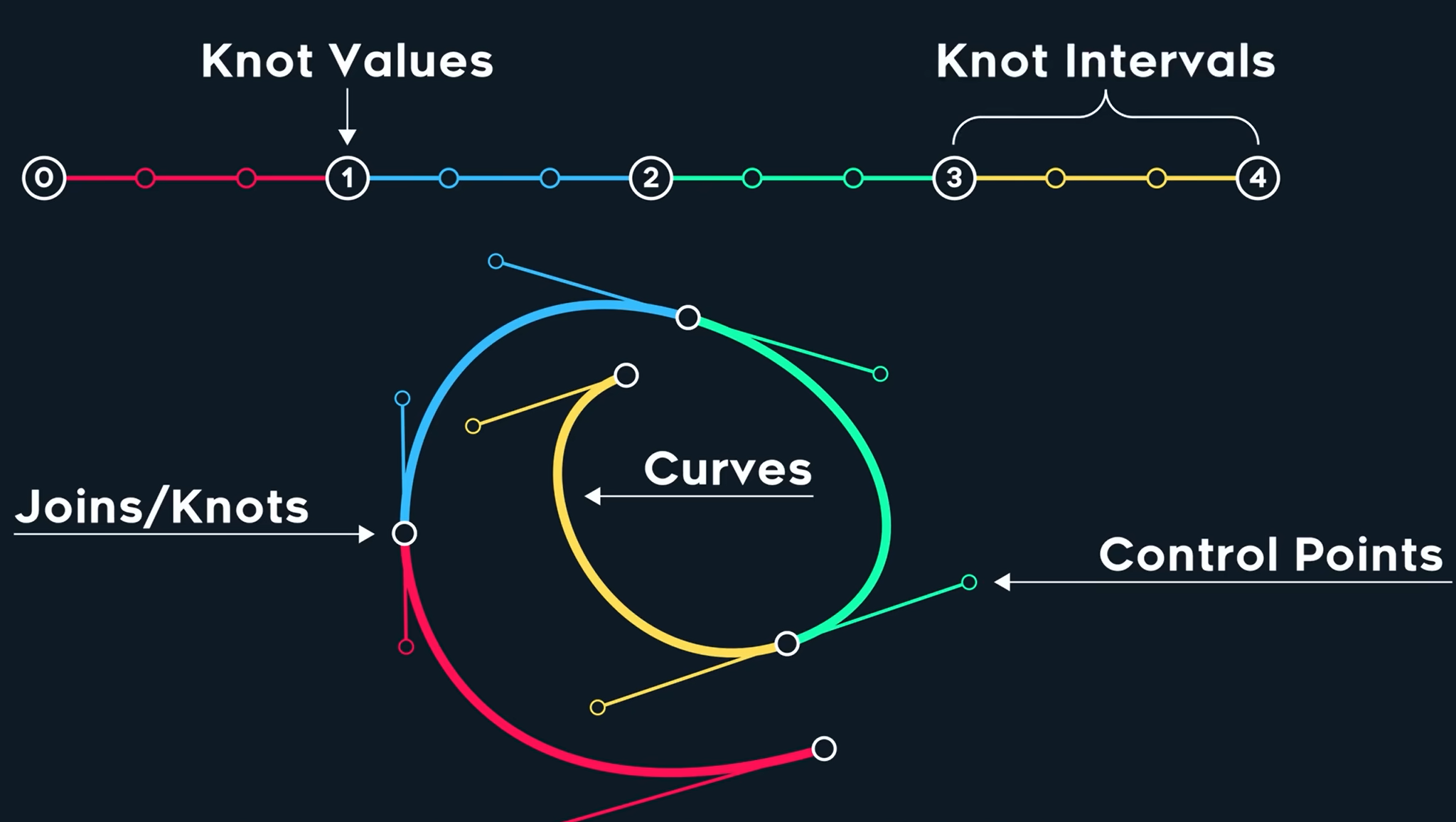
分段之后可以进行局部控制，三次贝塞尔曲线。四个点就可以控制任意曲线，首尾相连的多个三阶贝塞尔曲线就可以获得任意想要的连续曲线，只需要每过三个点的末尾设置为曲线的接触点。

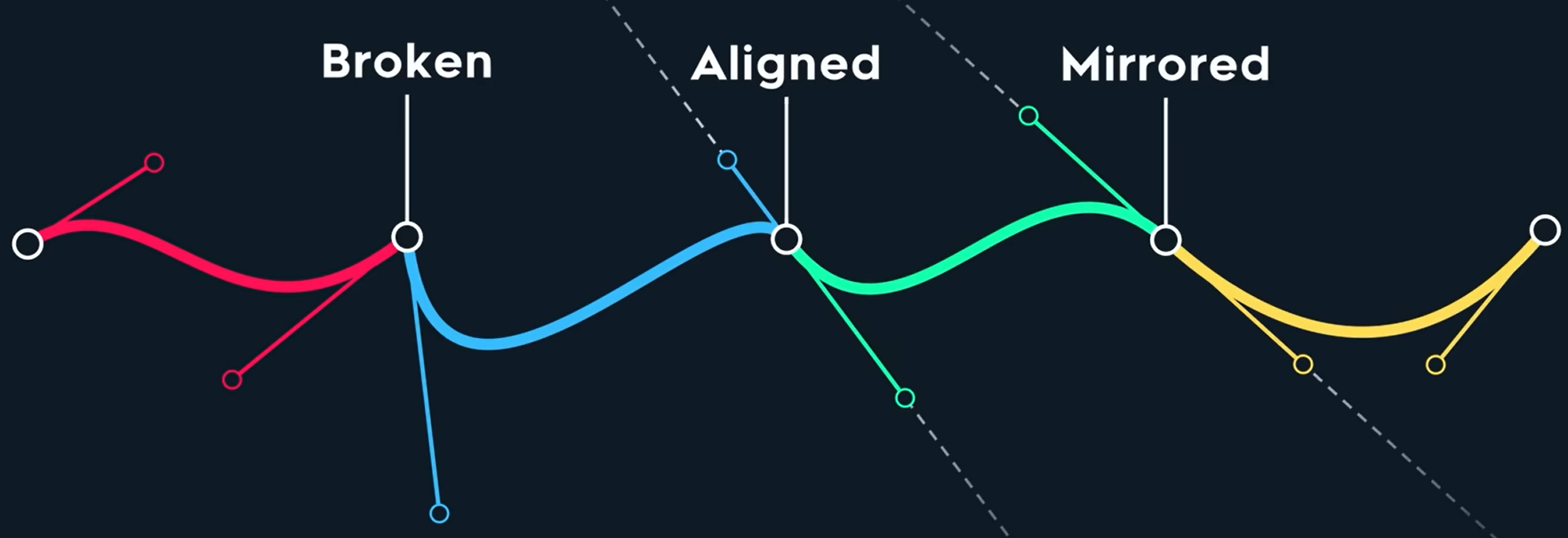
分如上三类，Broken、Aligned、Mirrored（镜像）。knots点相切的时候，曲线会变得平滑。

连续

这是C^0连续的，但分开就不是

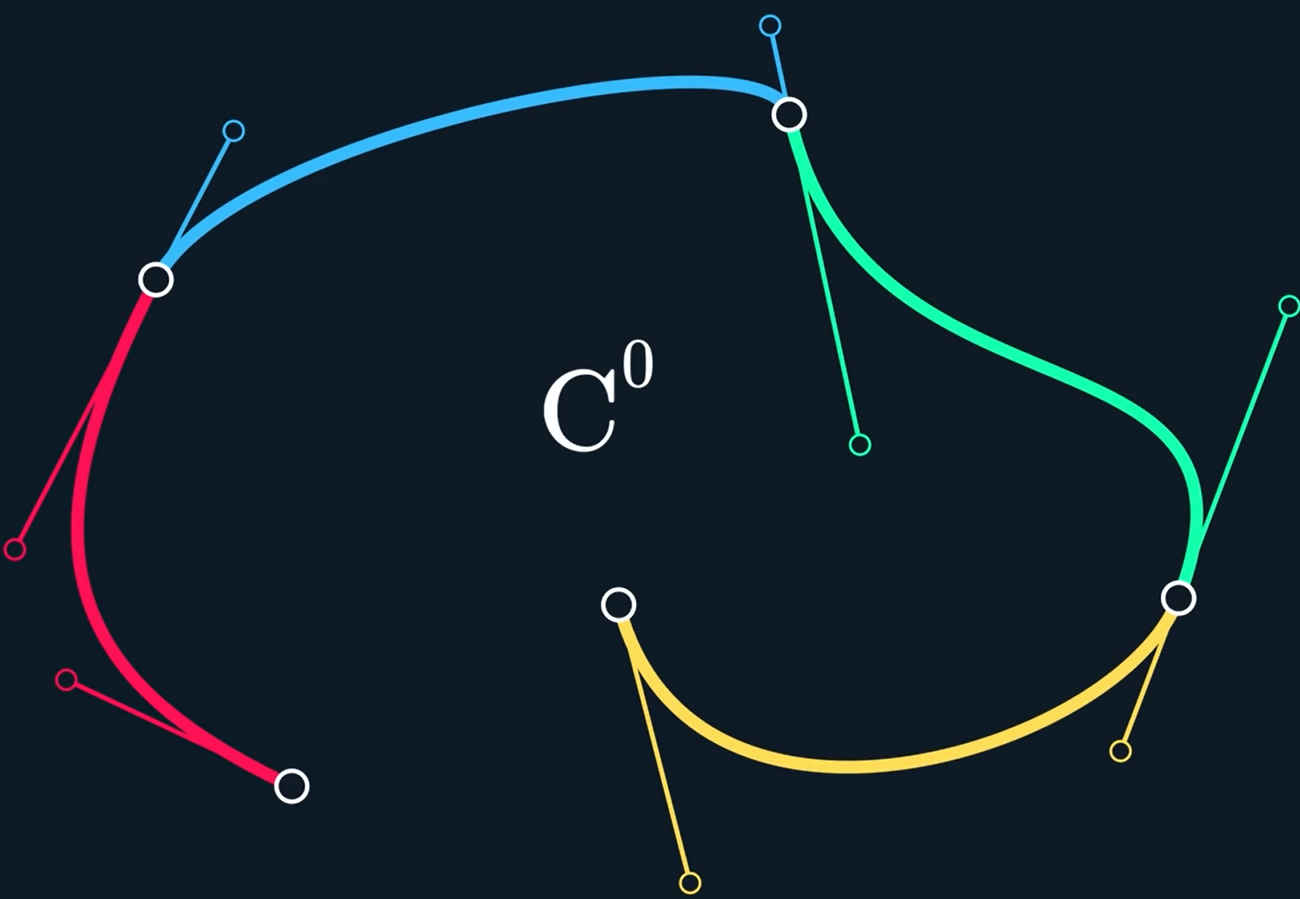
一阶导其实表示的是速度，我们可视化速度可以发现尽管像上图一样进行knots点是相切的（Aligned），但速度还是不一样

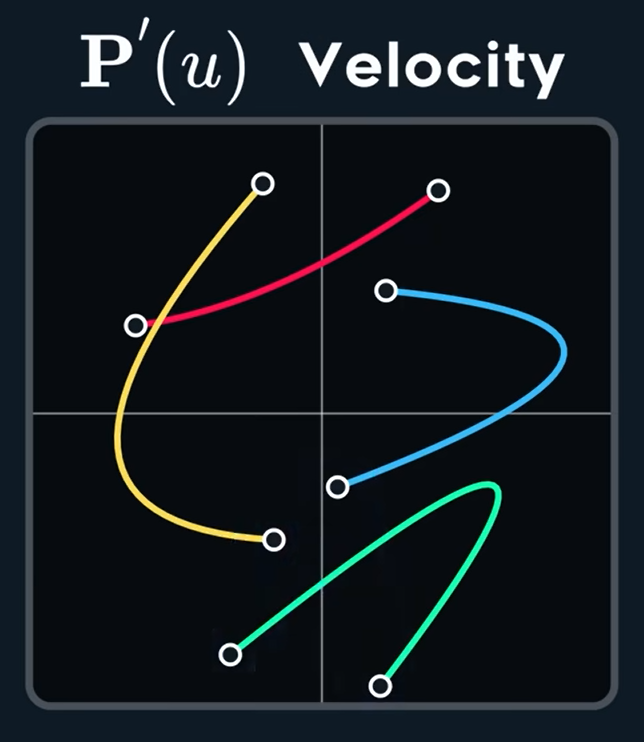
其实这也就表明了此时一阶导（速度）是不连续的，这也就是C^0连续，那么什么时候C^1连续呢？那就是Mirrored时候

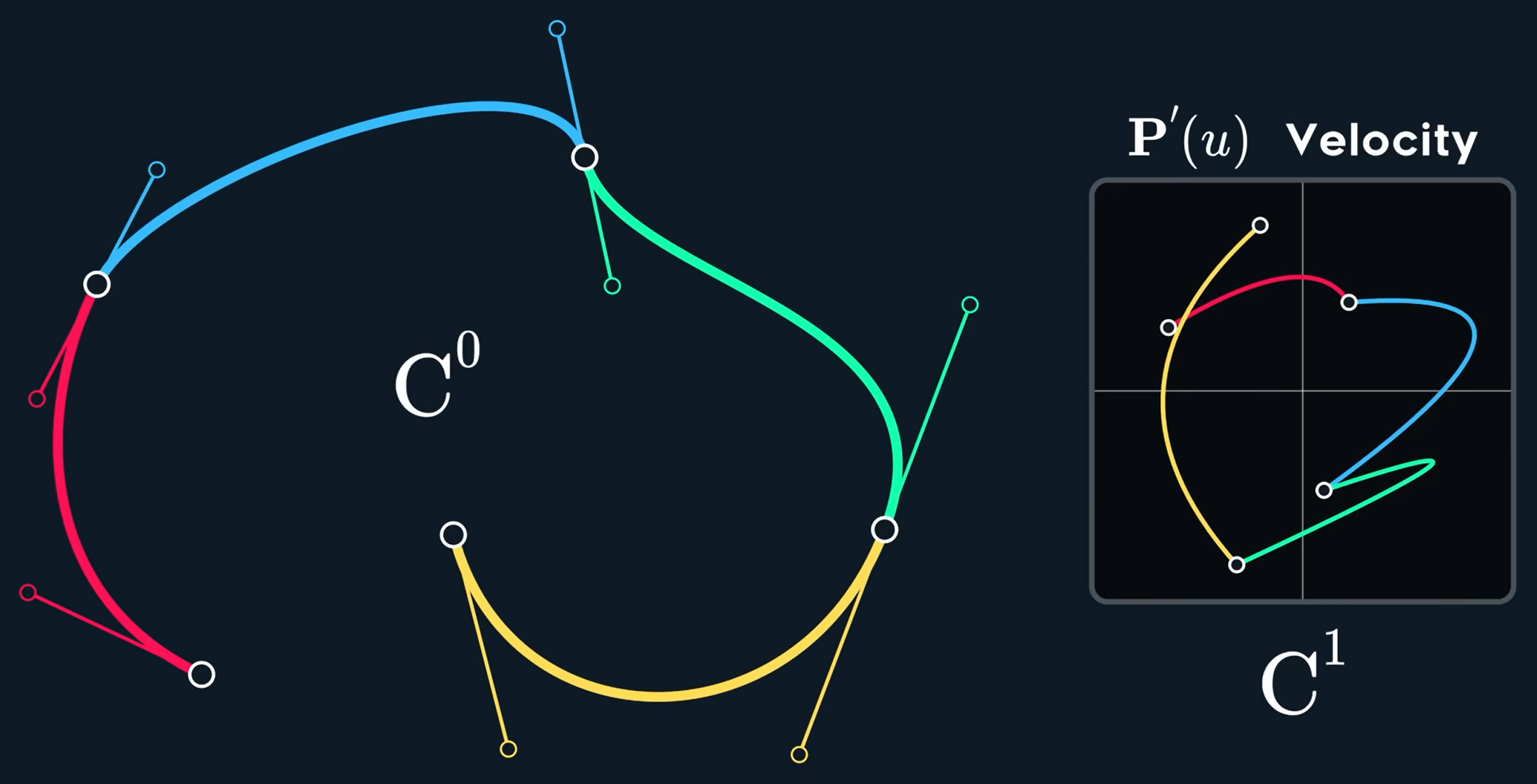
C^2连续要求加速度也要连续：

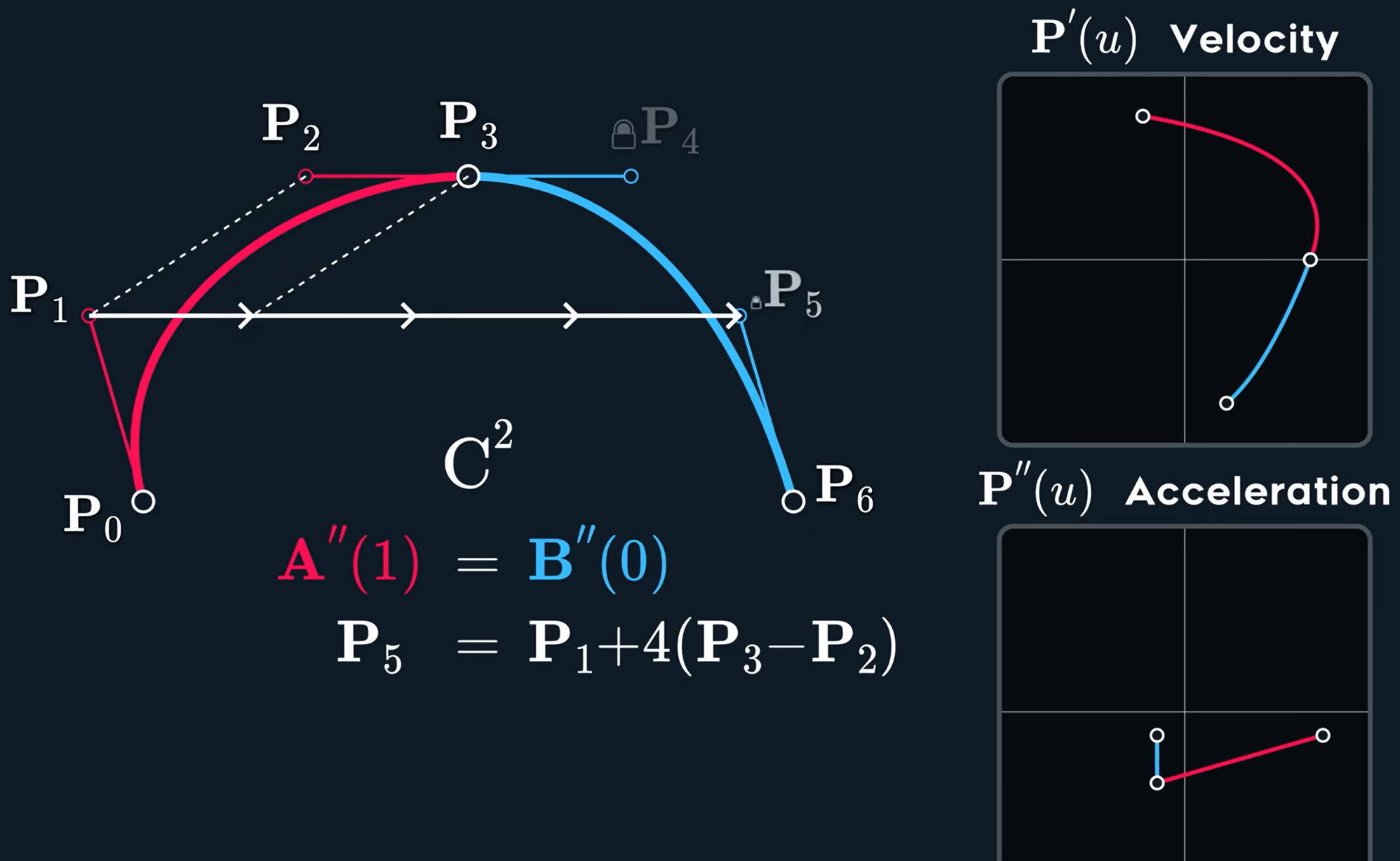
其实对于C^1连续的时候，我们要求P_3点要连续，也就是要求

\begin{aligned}
\mathrm{A}'(1)&=\mathrm{B}'(0)\\
\mathrm{P}_4&=2\mathrm{P}_3-\mathrm{P}_2
\end{aligned}

也就是说，\mathrm{P}_4是由\mathrm{P}_2,\mathrm{P}_3来决定的,这样才会得到\mathrm{A}'(1)=\mathrm{B}'(0). 那么如果是二阶导（加速度）连续呢，就是如图的式子，此时\mathrm{P}_5也被固定住，由\mathrm{P}_1,\mathrm{P}_2,\mathrm{P}_3决定。

那么为了使得整个曲线都有C^2连续，那么其他连接处也要有这些连续性约束

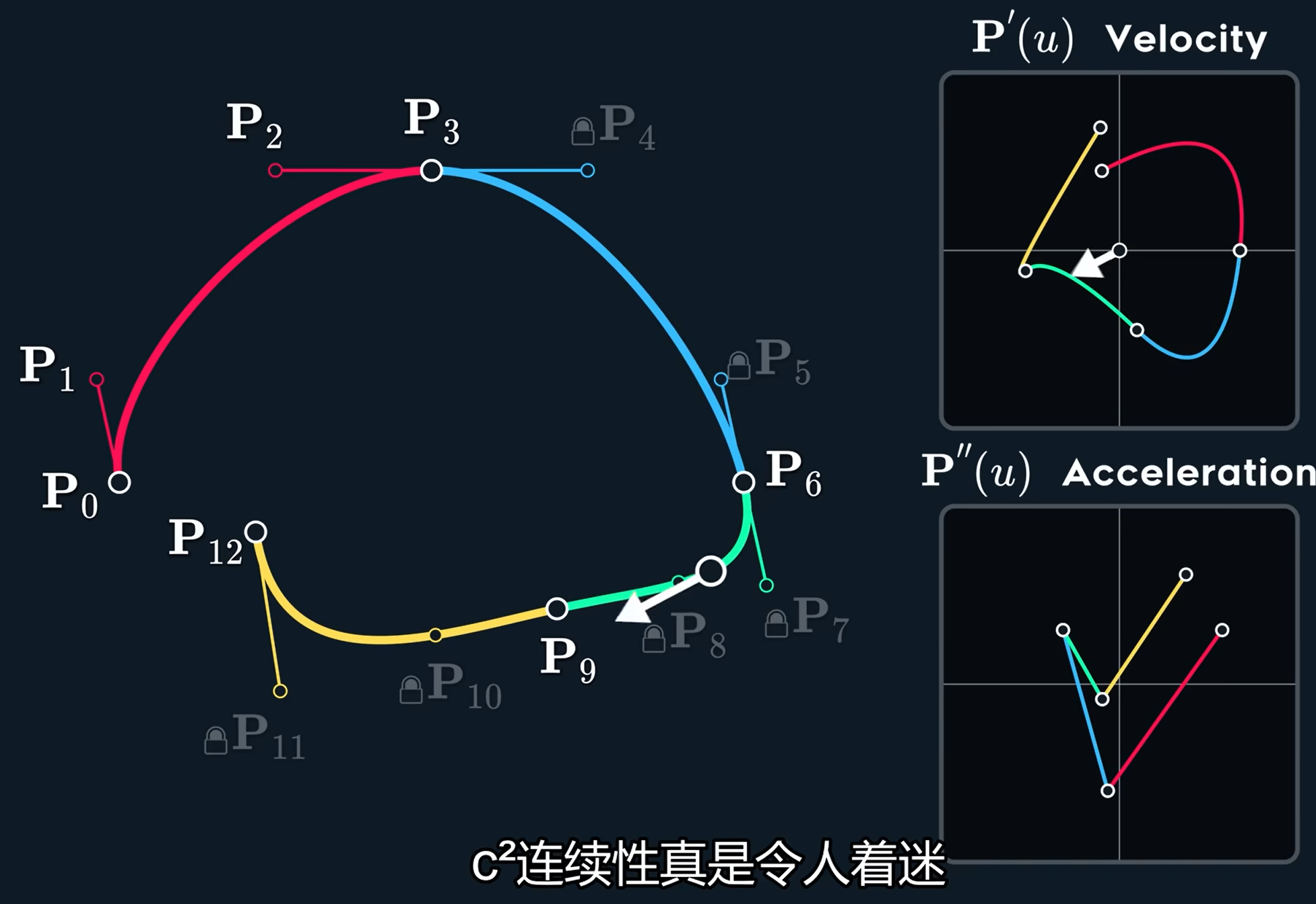
但无法做到C^3连续，长话短说——\mathrm{P}_6的位置被完全决定

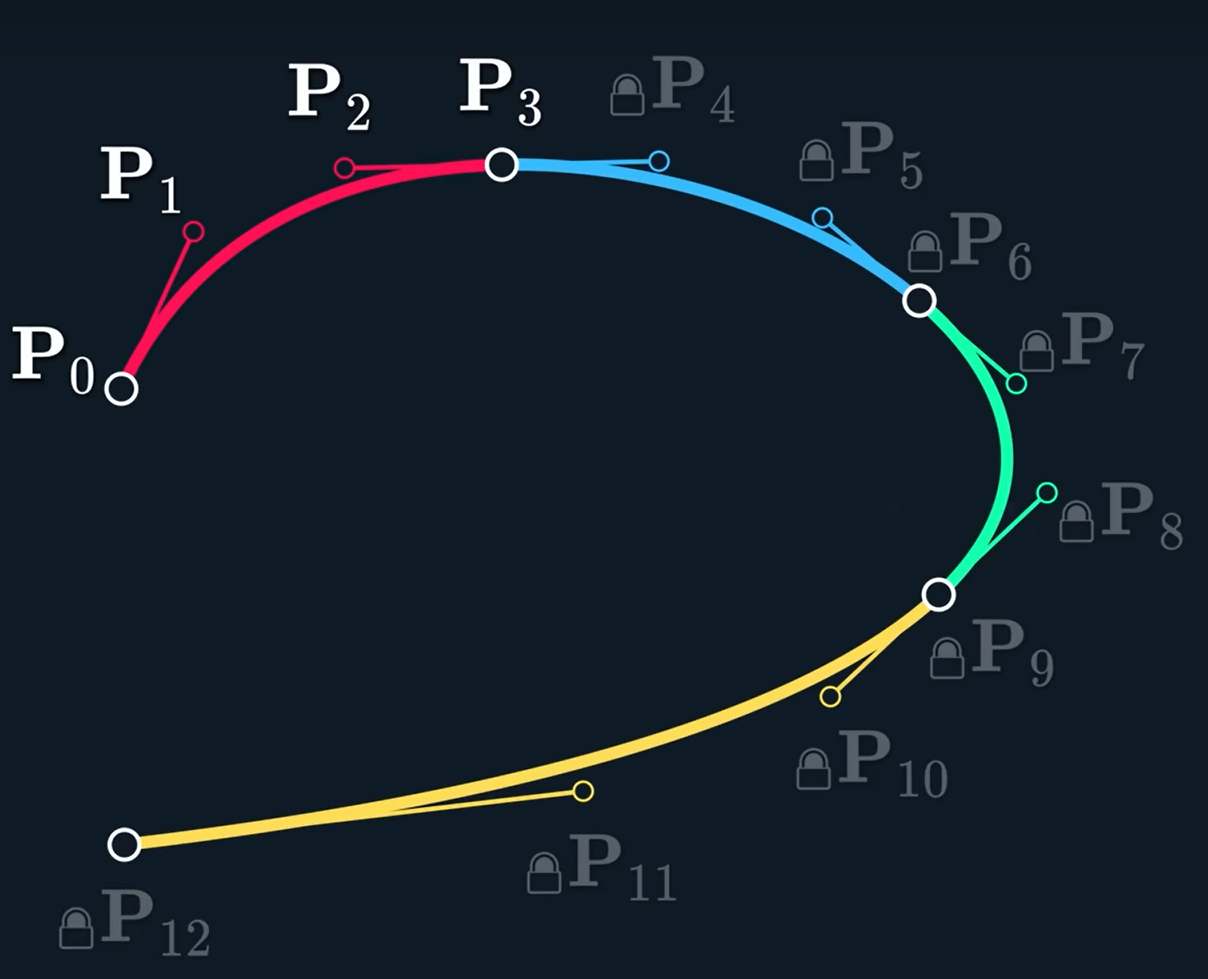
只能控制初始的一小段，例如移动\mathrm{P}_1的话，整个曲线会被影响得很大！

几何连续

如果不关注速度的大小突变呢？只关心切向，我们可以通过简单将速度向量归一化来得到切向量

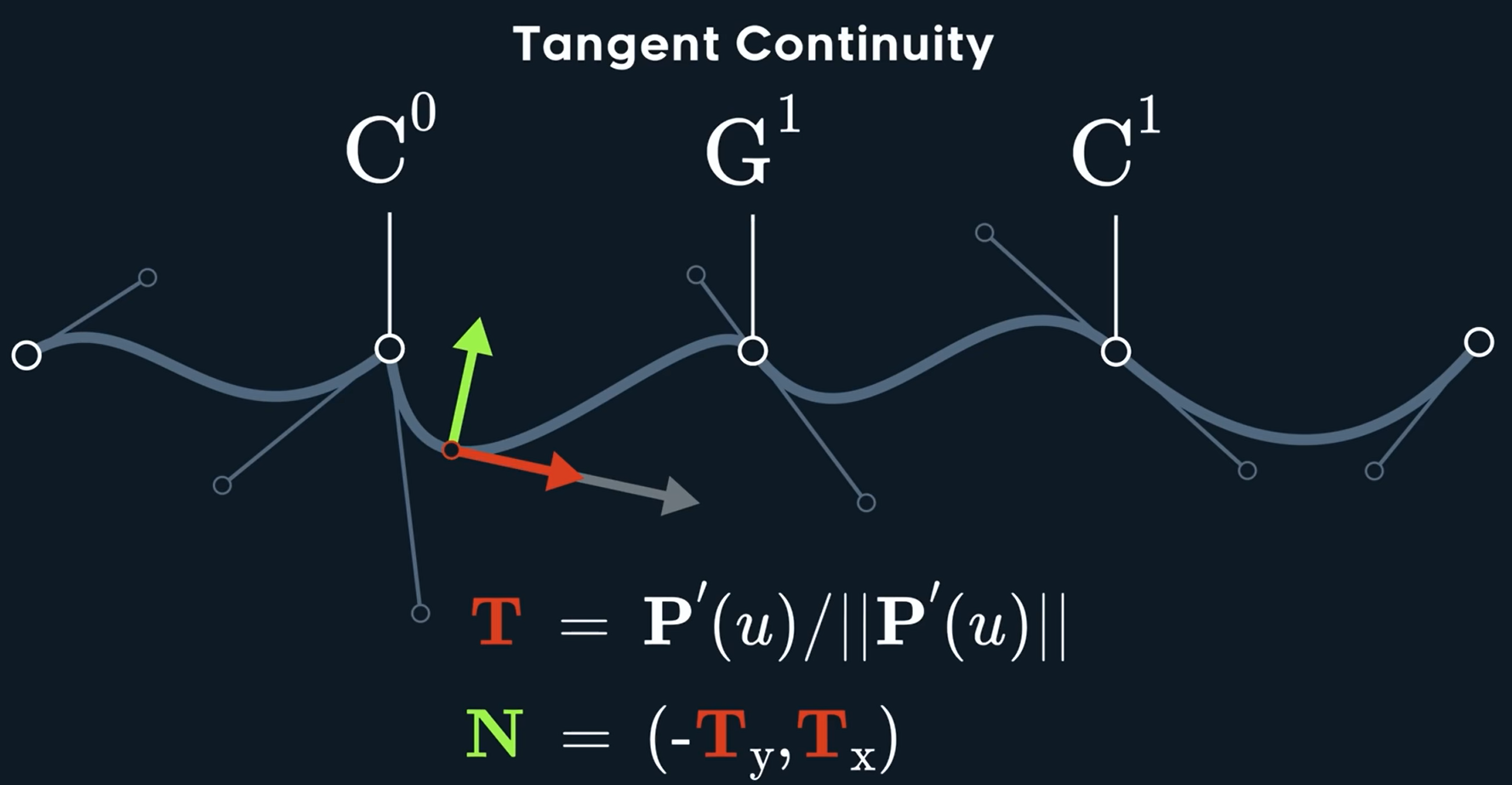
上面就是\mathrm{G}^1连续。如果仔细观察这些地方，发现尽管看起来对齐了但还是有很大的缝隙，可以从曲率的方面来看

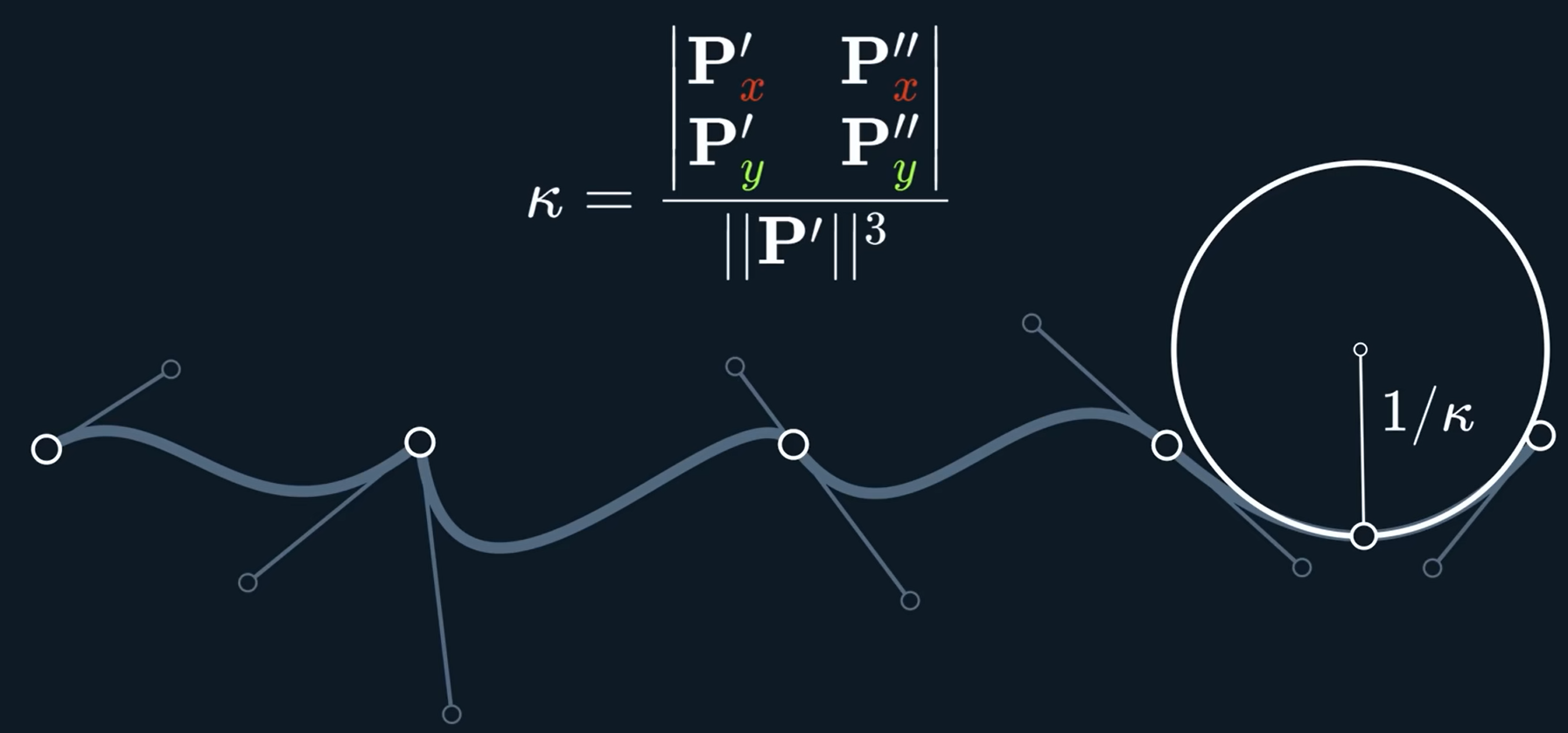
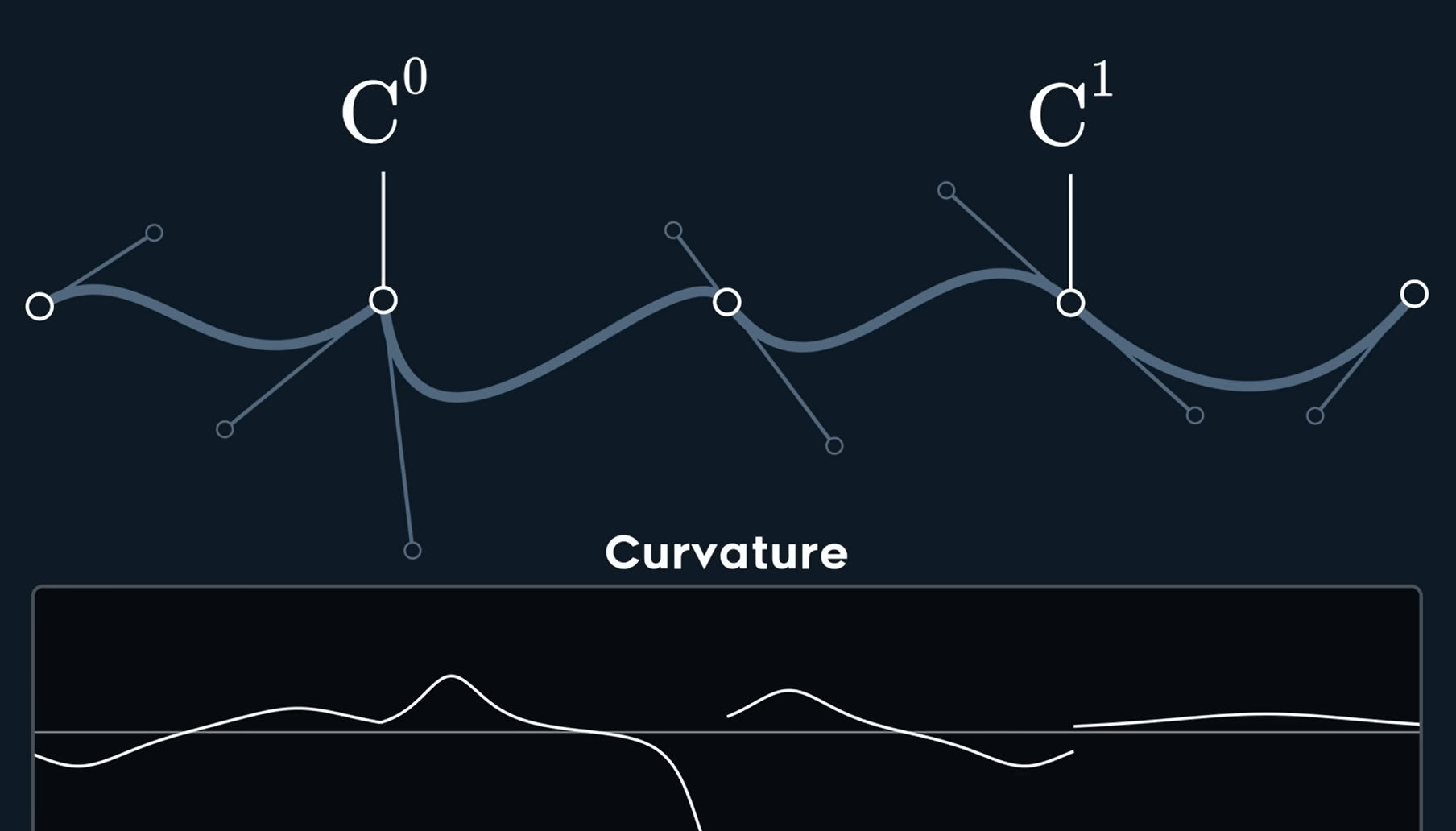
可以发现尽管是C^0,C^1连续，曲率差别还是很大

这叫曲率梳，如果我们限定\mathrm{P}_4和\mathrm{P}_2,\mathrm{P}_3一个方向，并且给一个自由度\beta，我们可以发现还并未连起来，但是如果我们再对\mathrm{P}_5进行限制（如图），此时无论怎么变化\beta_1,\beta_2的话，它们都接起来了，如图\mathrm{P}_3的上面。移动控制点也同样有效。

但仅在连接处拥有连续的切线方向还不够。

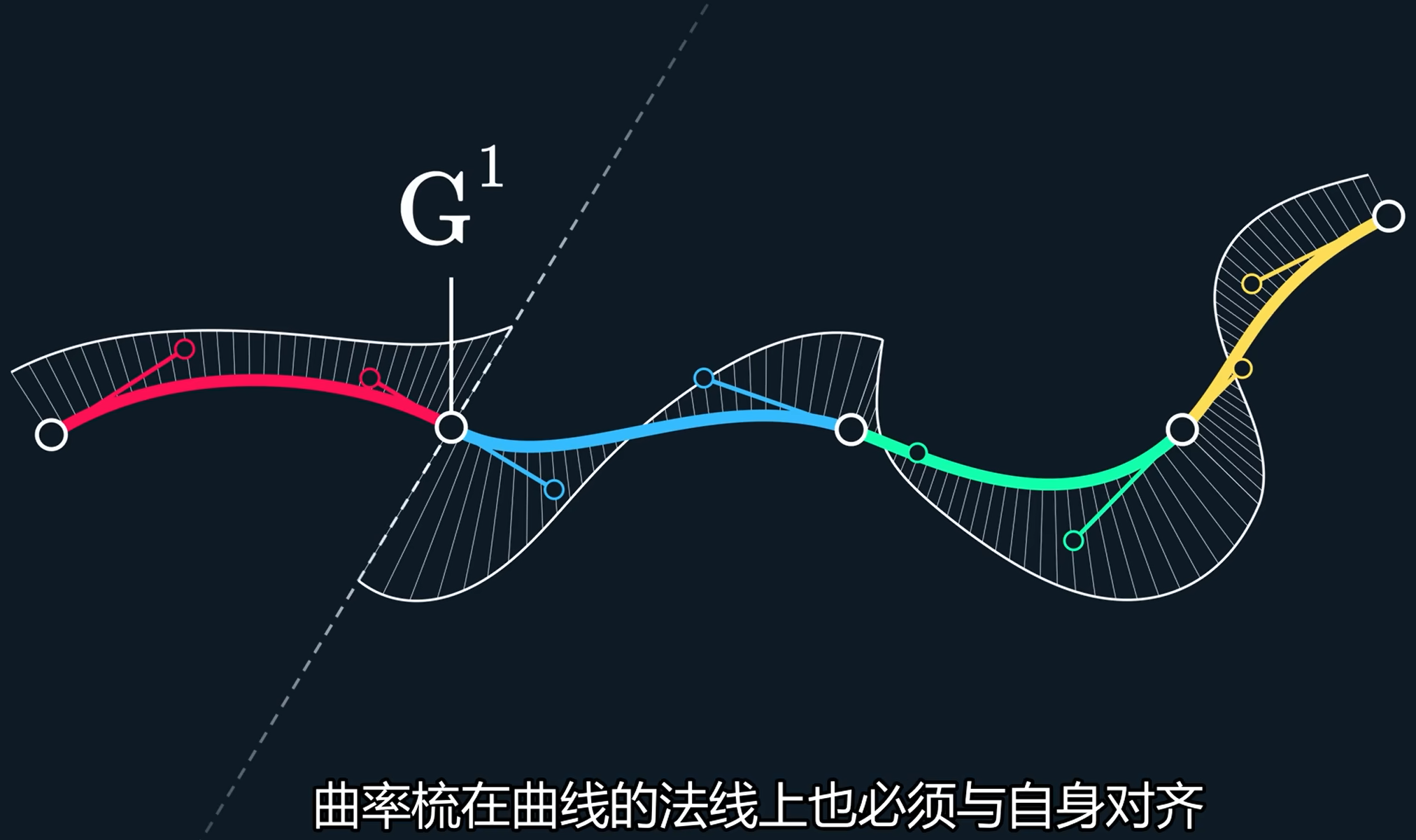
G^1表示切线是连续的，曲率梳在曲线的法线上也必须与自身对齐

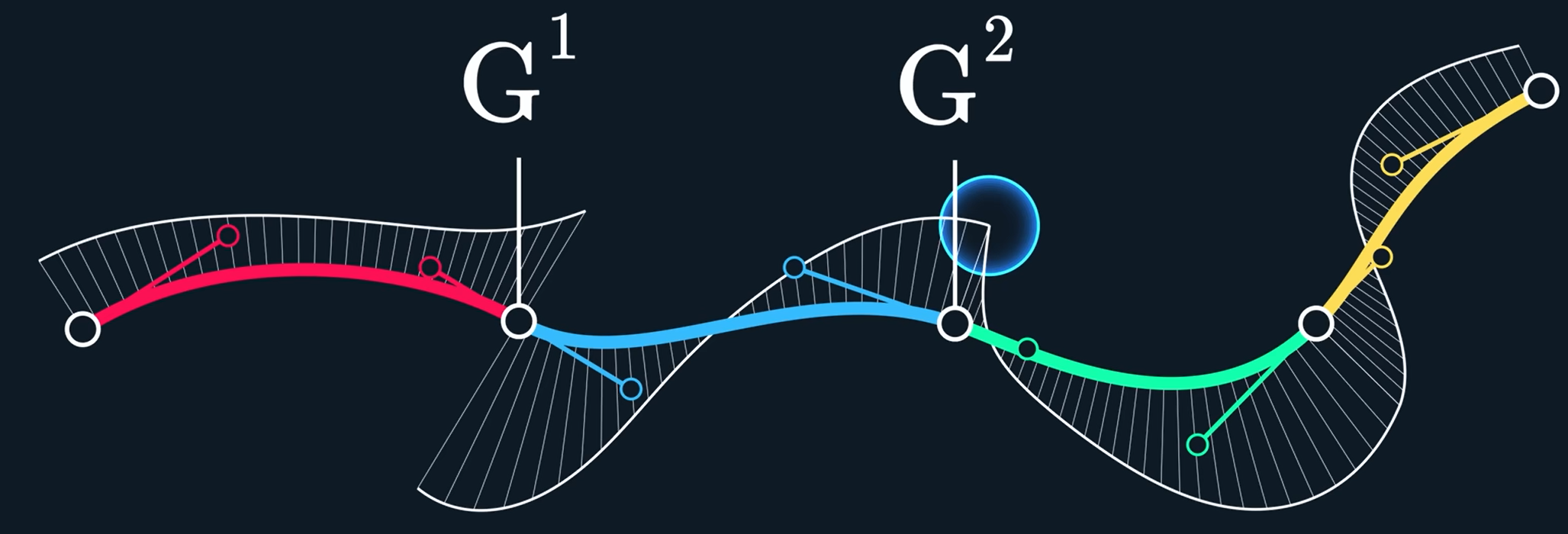
G^2表示曲率是连续的

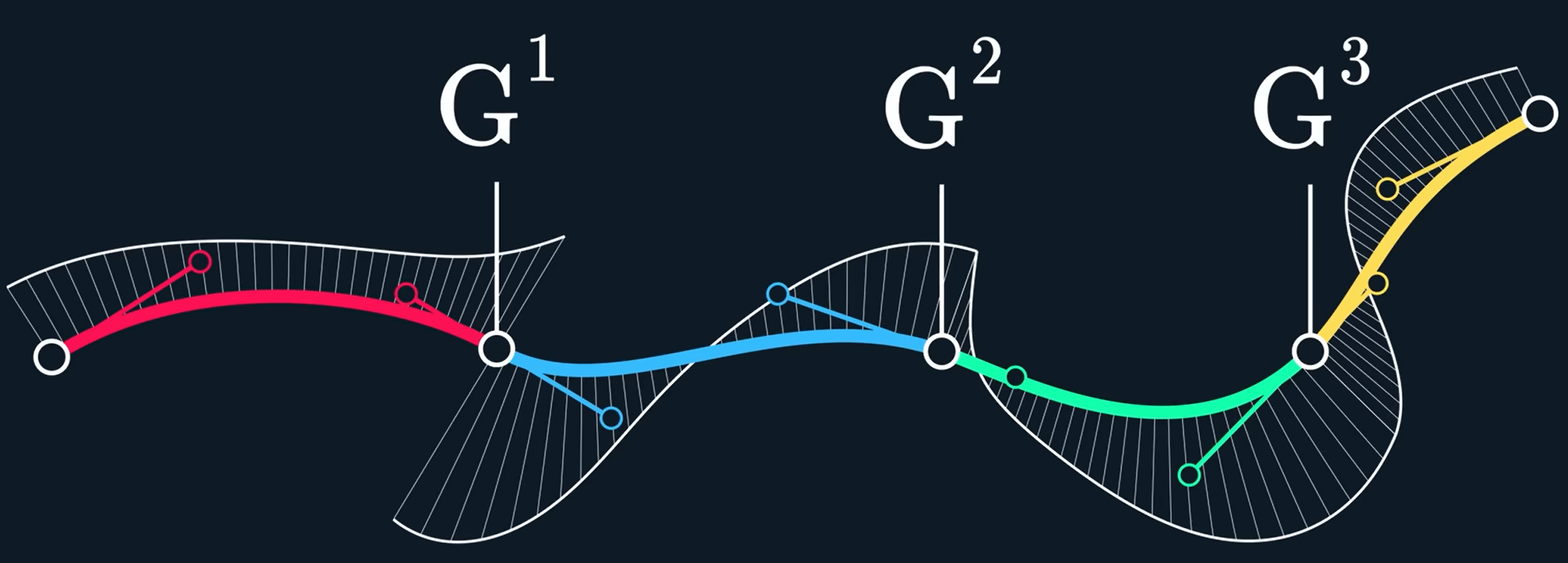
G^3表示曲率的变化率是连续的

如果存在一个函数g(t)，使得A(t)和B(g(t))是C^n连续的，那么它们就是G^n连续的

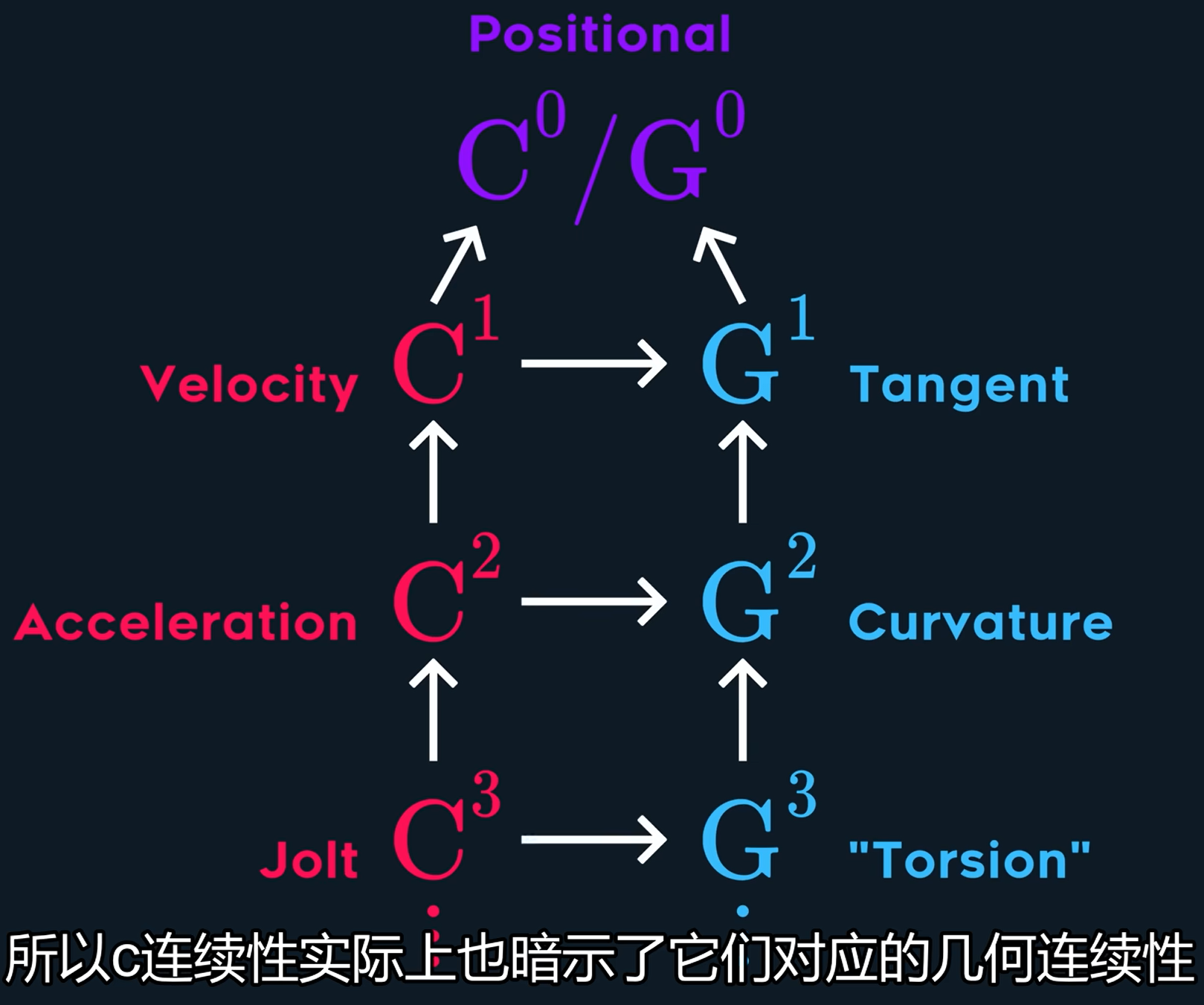
C^1连续也必然是G^1连续。

事实上，G连续要比C连续要宽松一些。

这些只在曲线是正则的时候，即\mathrm{P}'(t)\neq 0的时候

扩展宇宙其他样条

对于贝塞尔曲线而言，这些初始点有些不太好，如果给两个初始点都有速度会怎么样？

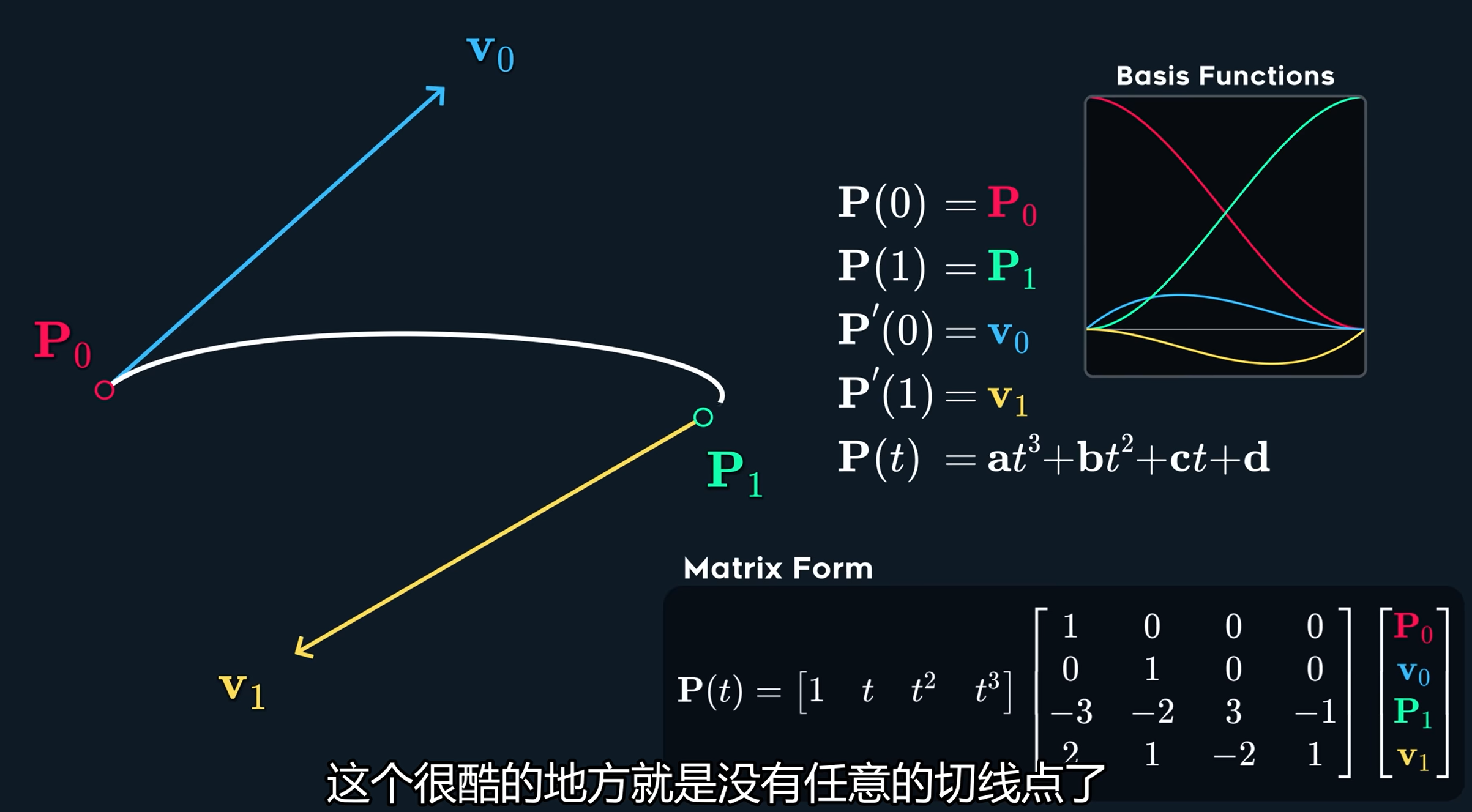
我们有如图的\mathrm{P}(0),\mathrm{P}(1),\mathrm{P}'(0),\mathrm{P}'(1)的四个初始条件，我们来求解

\mathrm{P}(t)=at^3+bt^2+ct+d

首先当t=0的时候，我们有\mathrm{P}(0)=d=\mathrm{P}_0，即

\mathrm{P}(t)=at^3+bt^2+ct+\mathrm{P}(0)

然后我们再利用\mathrm{P}'(0)，就可以解得c=v_0,其实也就可以求解出所有的，即上面的矩阵，这些也有叫基函数。

但是这样条曲线不符合C^2连续，只符合C^1连续，因为速度是匹配的，但是加速度\mathrm{P}''(t)是不匹配的。

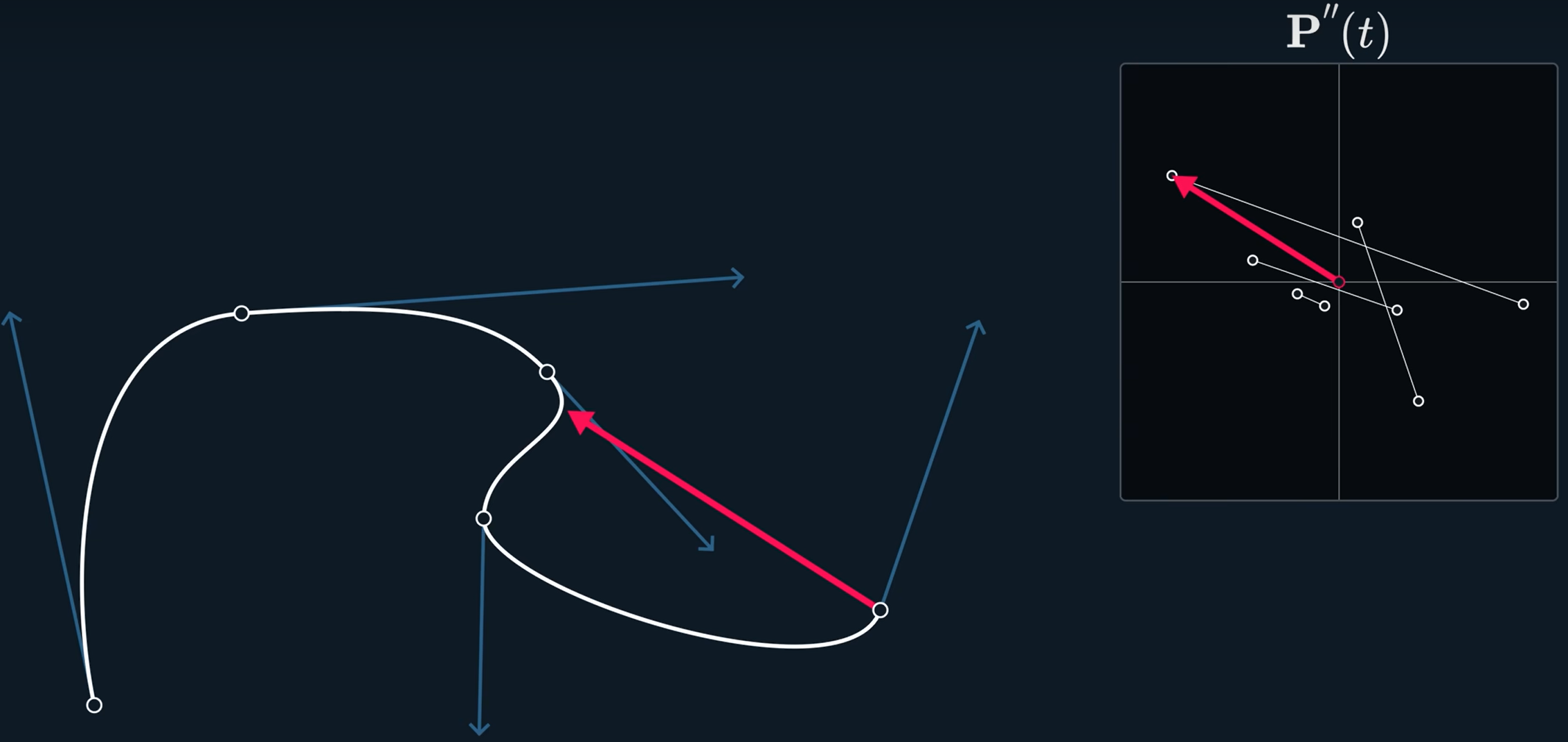
这个叫Hermite Spline。

Hermite样条允许在连接点有两个速度，一个用于进入一个用于离开。

事实上Hermite样条和贝塞尔曲线有很相似的地方，如果把每个速度除以三并加上源点，就可以得到贝塞尔切线点。

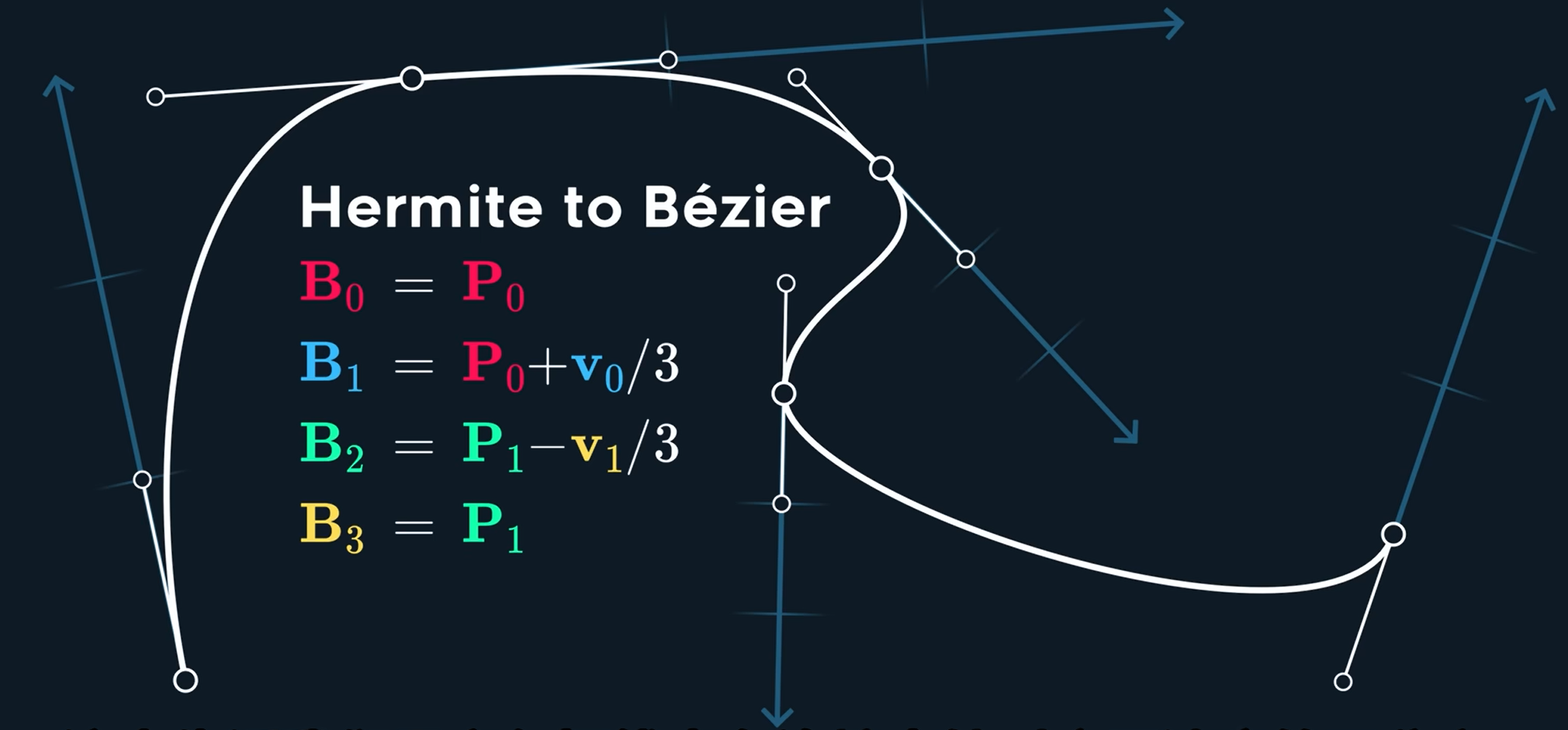
如果我们对于每个点不使用我们的初速度，而使用相邻的两个点的向量作为我们的初速度

重复操作，并且对于初始点做一个镜像（因为初始点还没有相邻的两个）

这样看起来形状很奇怪，有些地方很平坦，有些地方很急剧变化，可以看到这个曲率梳如下：

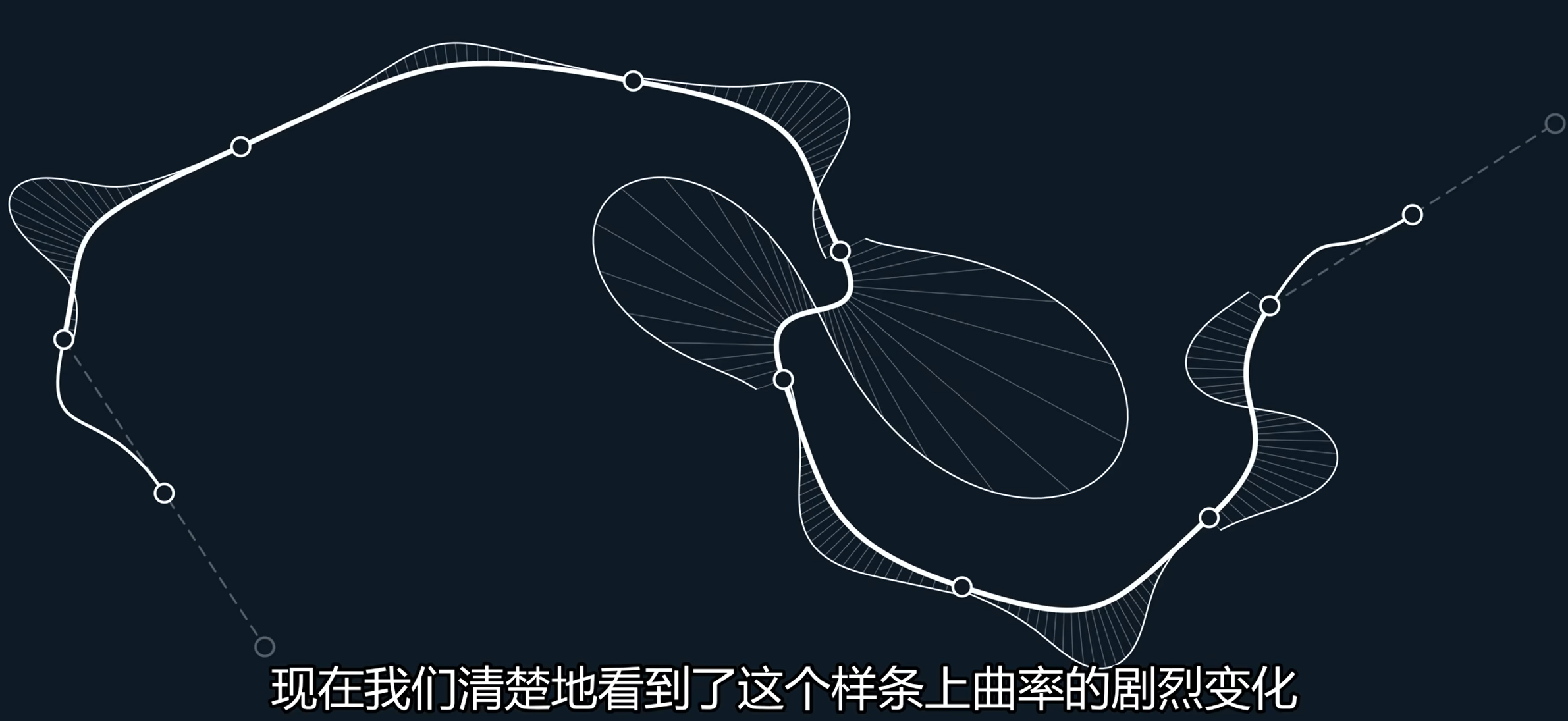
应该要找一种方法来减轻这些急转弯和平坦段的地方。如果对于每个速度都有一个缩放sacle，随着scale减小看起来平缓了但继续下去会接近于线性样条曲线。

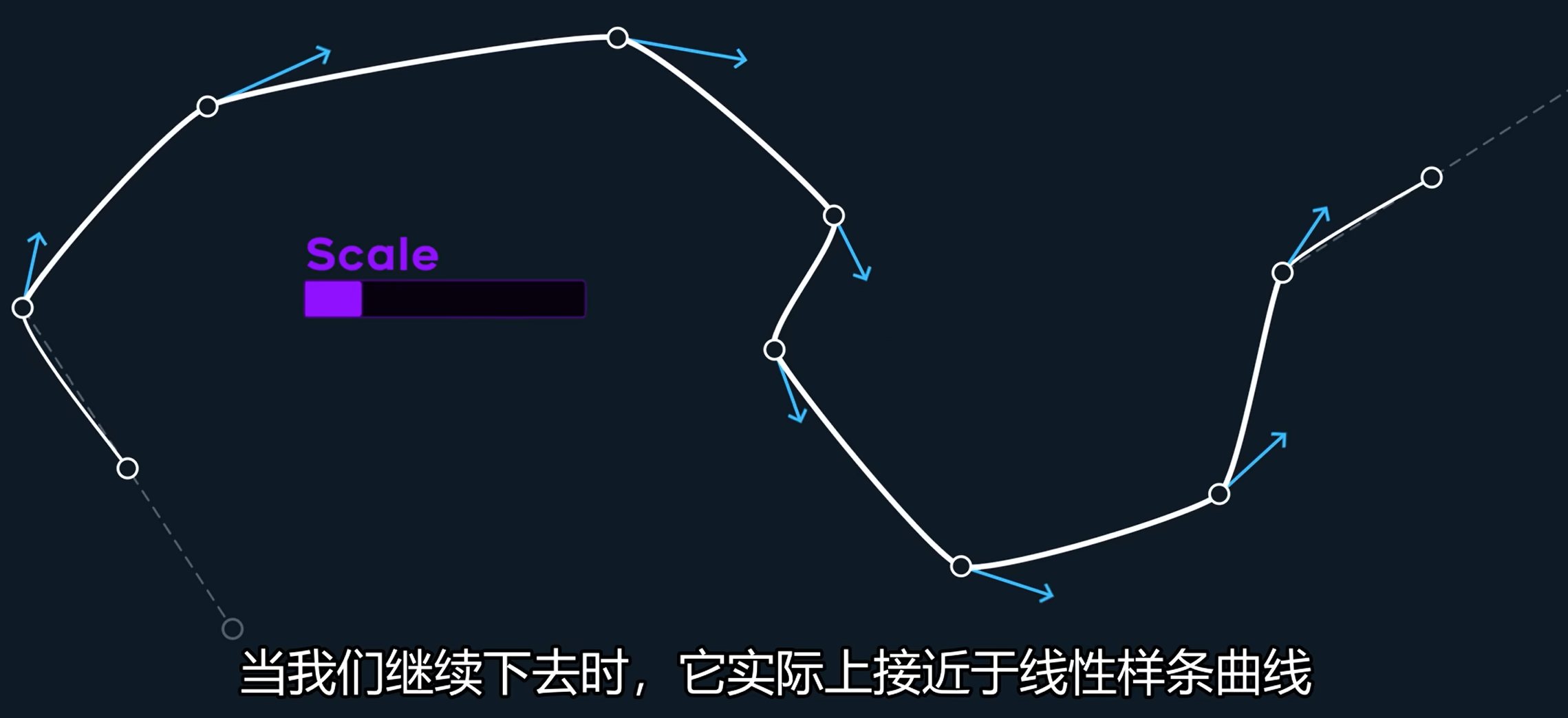
这个时候的曲率梳看不得，在端点处极大突出的变化

这个叫Cardinal Spline，基数样条。

其实放在1/2的时候还是挺好看的。此时叫Catmull-Rom Spline

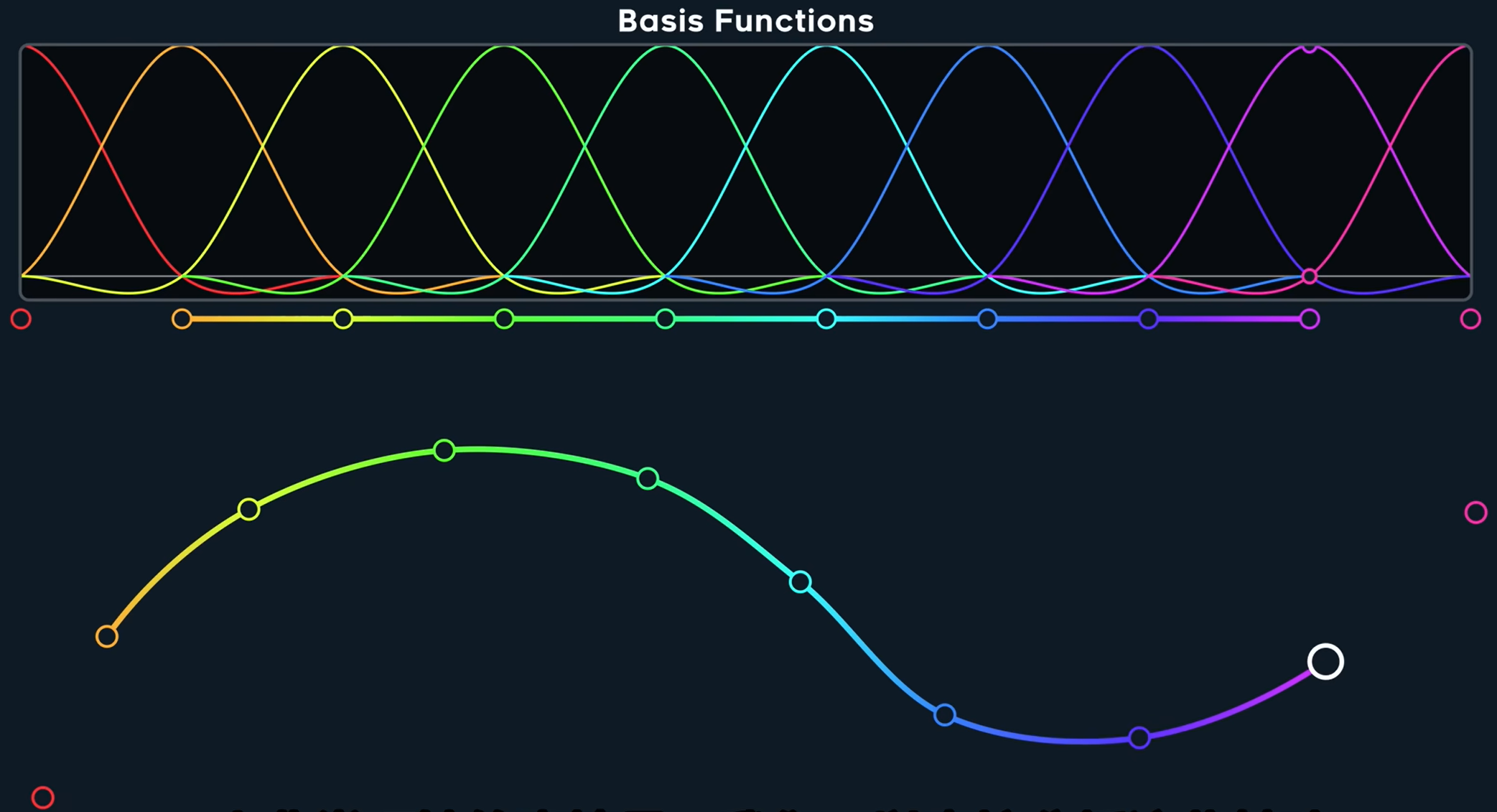
可以直接分析这些性质

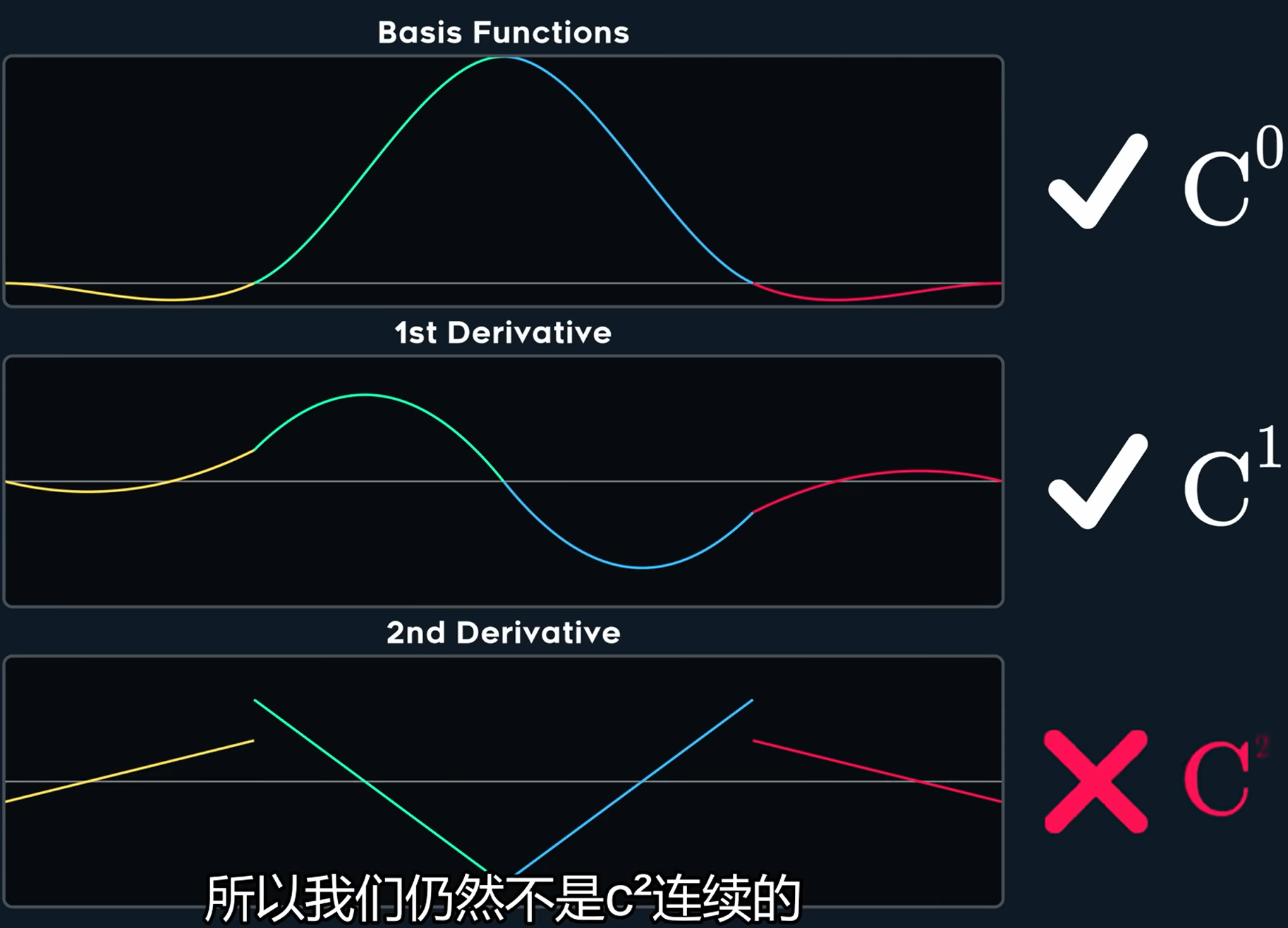
那么是否能做到一个C^2连续的样条呢？

那么16个未知数就需要16个方程！

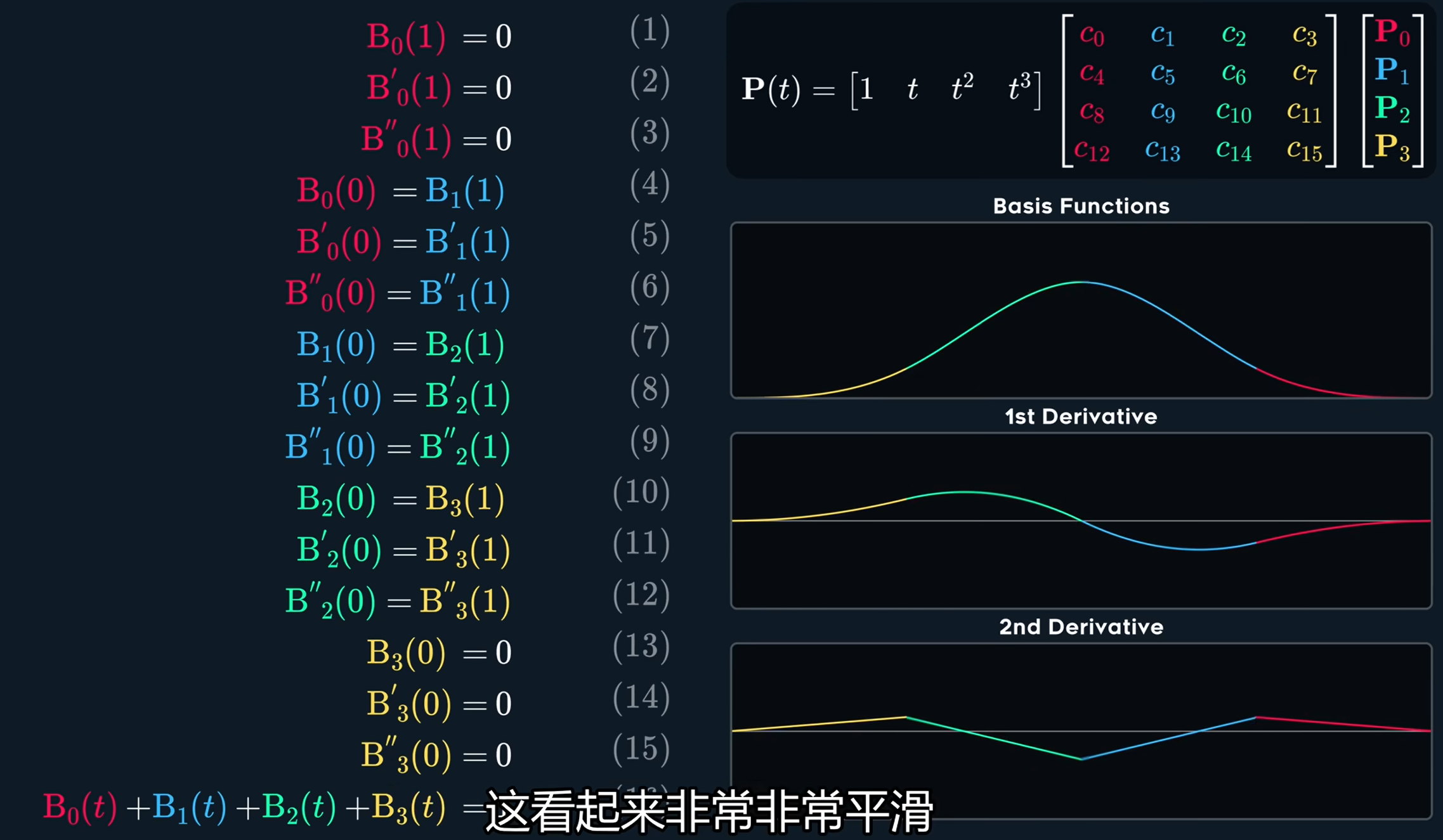
最后一个是凸组合，相加为1

我们来看一个，其实曲线和控制点并不重合

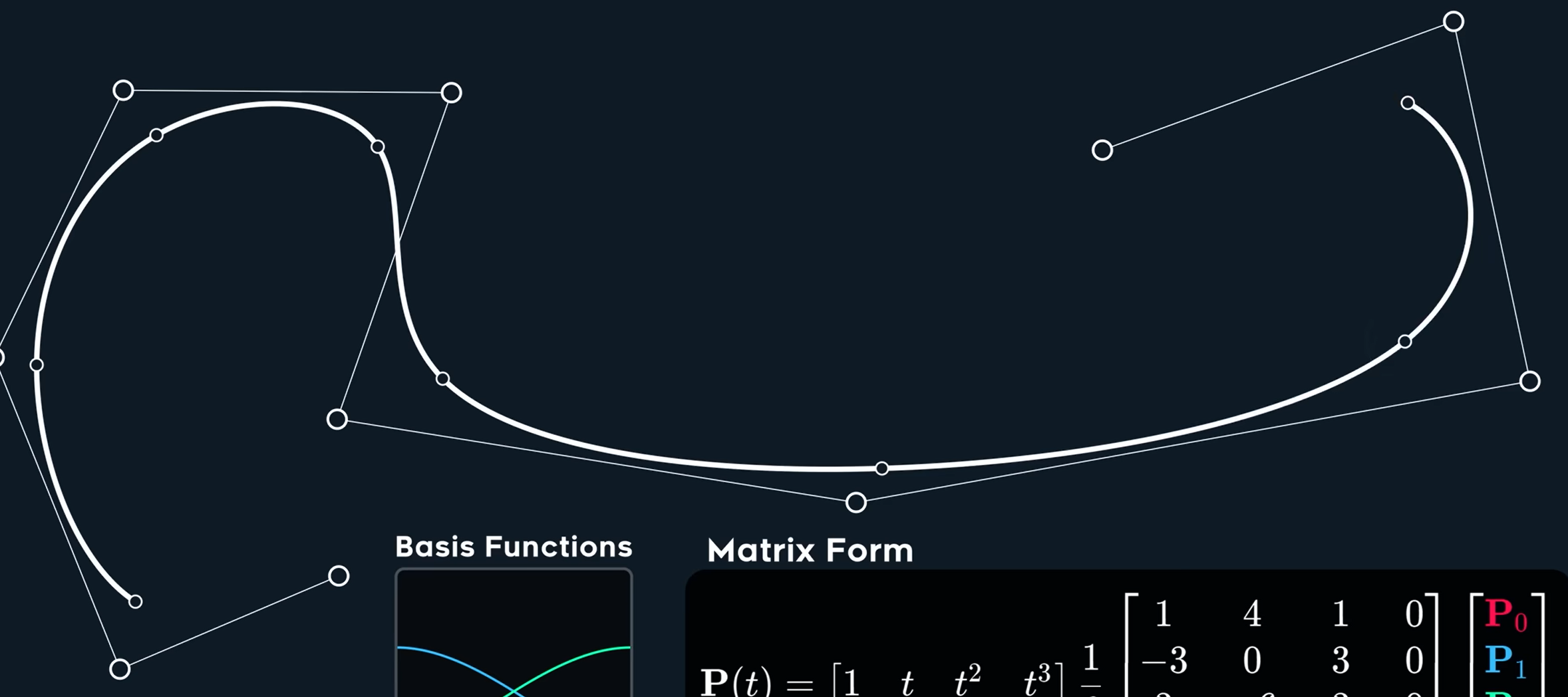
几何连续性看起来非常好，但也不是G^3连续的（因为曲率曲线本身并不是切线连续的）

这是G^2,C^2连续的，它有一个大名鼎鼎的名字——B-Spline！也就是我们的B-样条！

请记住一点——曲线本身并不是样条，它们是由样条生成的，重点在于多个曲线如何连接以及它们能够平滑地连接。

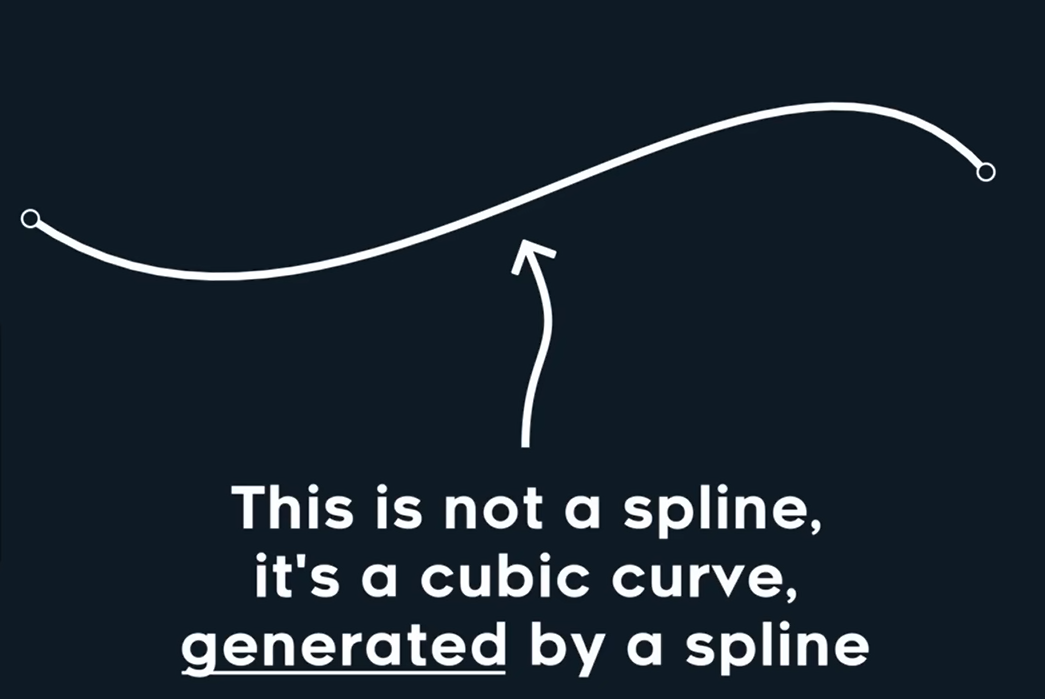
样条实际上描述的是控制点的变换。给定一些控制点你可以使用样条生成曲线。

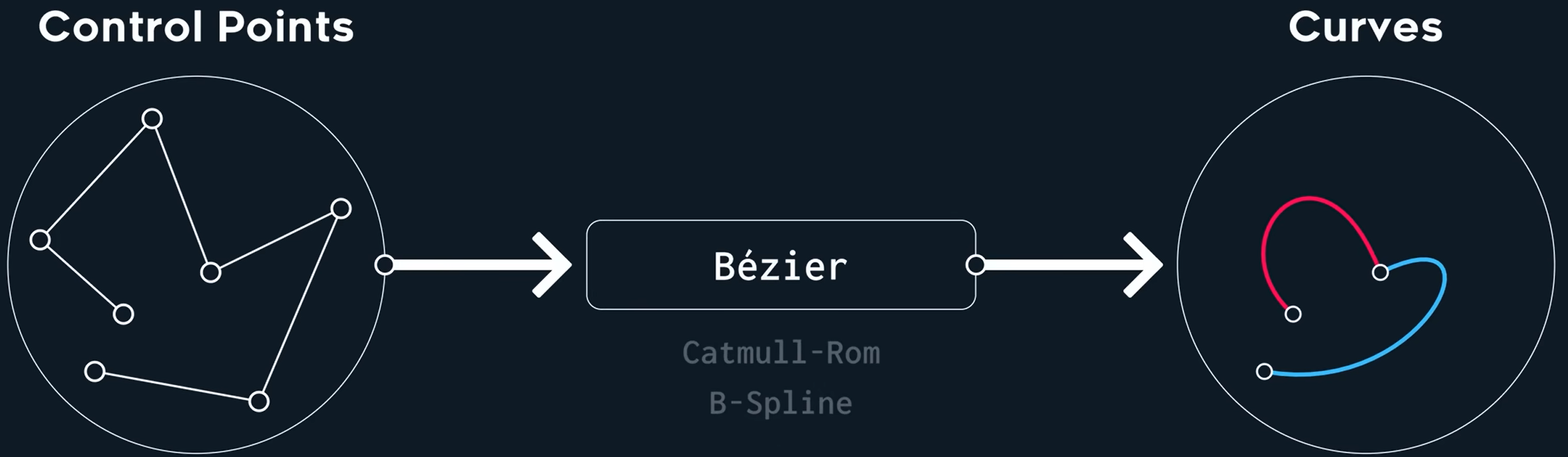
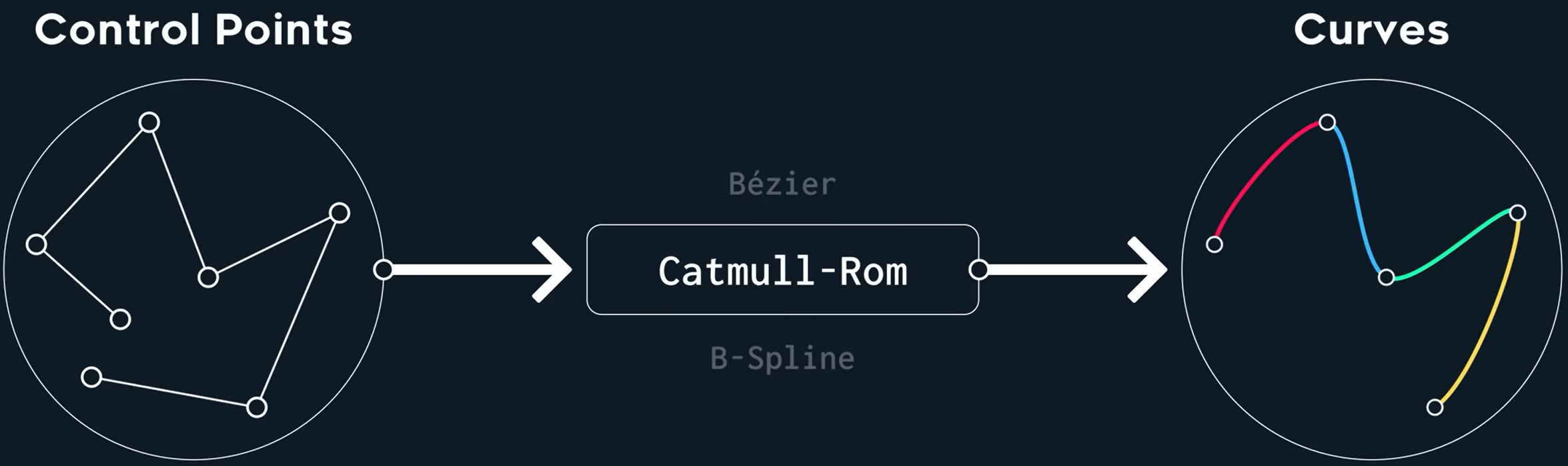
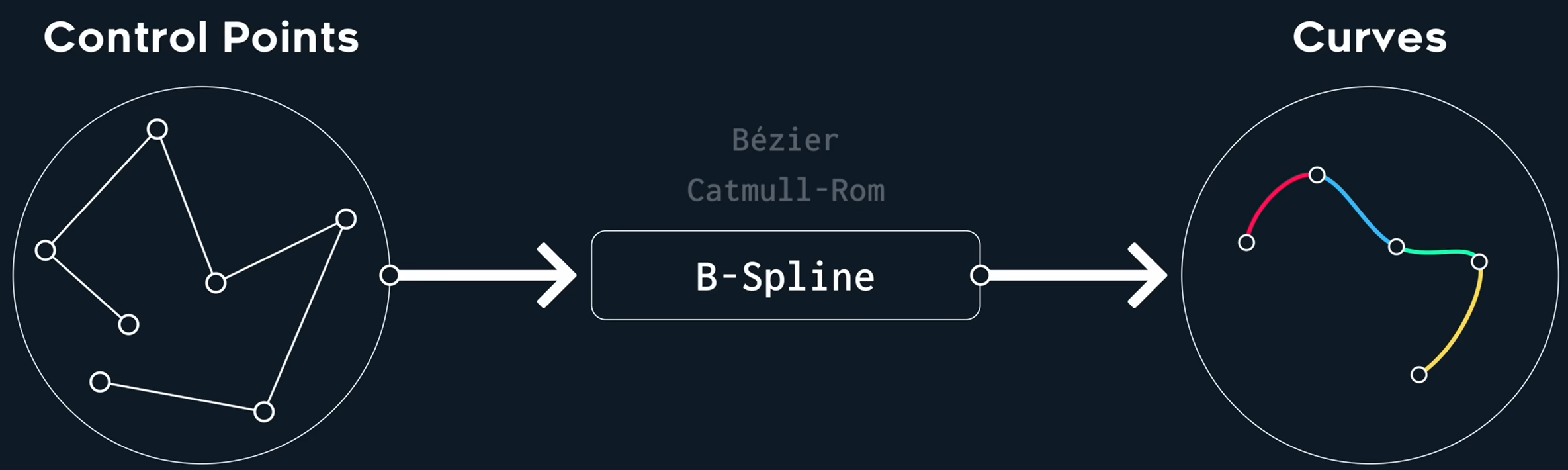
样条应该是产生曲线的生成器，它对曲线连接的连续性以及如何处理输入的控制点有一定的承诺。

在视频的59:14的时候总结了以下表格，并展示了各种动画，很建议去观看。

名称	阶数 (Deg.)	连续性 (Cont.)	切线 (Tangents)	插值 (Interpol.)	使用场景 (Use cases)
Bézier	3	C⁰/C¹	手动	部分	形状、字体和矢量图形
Hermite	3	C⁰/C¹	指定	全部	动画、物理模拟和插值
Catmull-Rom	3	C¹	自动	全部	动画和路径平滑
B-Spline	3	C²	自动	无	对曲率敏感的形状和动画，如相机路径
Linear	1	C⁰	自动	全部	平滑度不重要时的密集数据和插值

还有很多其他的，例如非均匀B样条，还有一个更高级的Non-Uniform B-Spline，即非均匀有理B样条

它允许控制每个控制点的优先级或权重，使曲线朝向或远离特定的控制点，这也就是大名鼎鼎的NURBS