基于顶点聚类的网格简化分析
摘要:本文实现了本课程的作业一——网格简化,使用的是顶点聚类的方法,使用了不同的合并新顶点的方法进行对比,并且尝试加入纹理贴图进行实验。
关键词:顶点聚类、网格简化、纹理贴图
一、实验内容
1.1 实验要求
实验要求为参考教材,实现一种网格简化的方法。在本实验中选择的是顶点聚类的方法。
1.2 实验目的
本实验目的如下:
1) 使用顶点聚类的方法完成网格简化
2) 对于生成新顶点选择不同的方法,有取平均值方法、取中值方法来选取的方法
3) 对于带有纹理图的mesh进行分析与讨论
1.3 实验环境
操作系统:Windows 11
编程语言:C++
开发工具:Visual Studio Code、Visual Studio 2022
其他相关库:glm库、OpenGL
二、实验程序
2.1 程序结构
本实验程序分为两个,一个是对于数据进行读入、处理最后输出成新的关于mesh的文件,另一个则是可以进行纹理贴图的渲染。前者为单文件,后者为项目类多文件。本报告主要对于前者进行讲述如何进行的网格简化处理。
值得注意的是本报告使用数据是OFF文件。
2.2 文件读入
2.2.1 数据存储结构
| 类名 | 作用 |
|---|---|
| Vertex | 存储点的三维坐标 |
| Face | 存储面的顶点下标 |
| BoundaryBox | 存储数据的所有点的最大和最小的xyz值 |
| Mesh | 存储整个mesh数据 |
本程序一共有四个类,分别是Vertex、Face、Boundary、Mesh类,见表2-1.
其中Mesh类有包含Vertex、Face的列表以及一个BoundaryBox(包围盒),并有计算包围盒的函数。这里主要展示这个类的代码。
struct Mesh {
std::vector<Vertex> vertices; // 若干面的信息
std::vector<Face> faces; // 若干点的信息
BoundaryBox bbox;
void computeBoundaryBox() {
bbox.minX = bbox.minY = bbox.minZ = 1e9;
bbox.maxX = bbox.maxY = bbox.maxZ = -1e9;
for (const auto& [x, y, z]: vertices) {
chkmin(bbox.minX, x);
chkmin(bbox.minY, y);
chkmin(bbox.minZ, z);
chkmax(bbox.maxX, x);
chkmax(bbox.maxY, y);
chkmax(bbox.maxZ, z);
} // 计算包围盒
bbox.lenX = bbox.maxX - bbox.minX;
bbox.lenY = bbox.maxY - bbox.minY;
bbox.lenZ = bbox.maxZ - bbox.minZ; // 获取包围盒边长
}
};2.2.2 读取OFF文件
本报告使用的是OFF文件,实现起来比较简单,主要是读入字符串的时候需要判断当前是v还是vt还是vn等,还需要将注释#除去。由于篇幅原因,这里仅展示处理面数据时的代码,完整代码请见代码文件。
bool loadOFF(const std::string& filename, Mesh& mesh) {
std::ifstream infile(filename);
... // 省略未找到和处理点的代码
mesh.faces.reserve(num_faces);
for (size_t i = 0; i < num_faces; ++i) {
std::getline(infile, line);
if (line.empty() || line[0] '#') { // '#'开头则是注释 需要过滤
--i; // 调整计数器,确保读取正确数量的面
continue;
}
std::istringstream iss(line);
Face f;
int vertex_count;
iss >> vertex_count; // 读入点的个数
f.vertexIndices.resize(vertex_count);
for (int j = 0; j < vertex_count; ++j) {
iss >> f.vertexIndices[j]; // 读入点的下标
}
mesh.faces.push_back(f); // 这个面加入到mesh中
}
infile.close();
return true;
}2.3 顶点聚类
2.3.1 划分区域
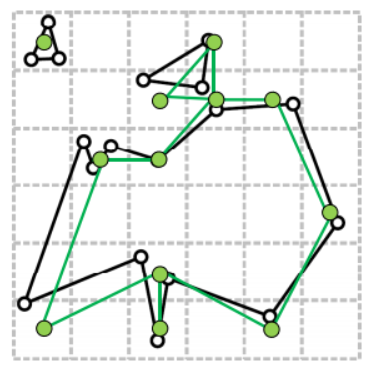
我们首先需要对整个空间划分若干个区域,如图2-1虚线区域所示,对于划分的每一个区域称其为一个cell。为了更加准确和有效的划分,这里给数据计算了一个包围盒(Boundary Box)通过mesh中的computeBoundaryBox进行。接着需要选取顶点聚类的程度,也就是需要调整cell的数量,通过和mesh点的关系构建。通过对于边界的微调可以得到每一个cell的长宽高,及包围盒的长宽高上cell的数量。
mesh.computeBoundaryBox();
int n = mesh.vertices.size(), f = mesh.faces.size();
int m = n * 0.8; // 构建一个关系
int cell_num = (sqrt3(m) + 1) / 2; // 构建关系
auto [nx, ny, nz] = modifyCellNum(mesh.bbox, cell_num);
float dx = mesh.bbox.lenX / nx;
float dy = mesh.bbox.lenY / ny;
float dz = mesh.bbox.lenZ / nz; // cell的长宽高
m = nx * ny * nz; // 新的点的最大数量此时的m就是理论上点的最大数量,因为并不是所有的cell都存在数据中的点,那么我们在处理之后还需要将无用的点进行删除,在后面会详细讲述。
现在我们拥有了在长宽高即XYZ方向上分别有nx,ny,nz个cell,我们对所有的cell进行编号,如图2-2所示。最下面一层则是首先按照x方向上进行递增,然后再对于y方向递增,当该层都编号完全之后换上方一层。这样我们很容易已知点的坐标(x,y,z),通过cell的长宽高可以得出此时的相对位置,即视以(dx,dy,dz)为新的基
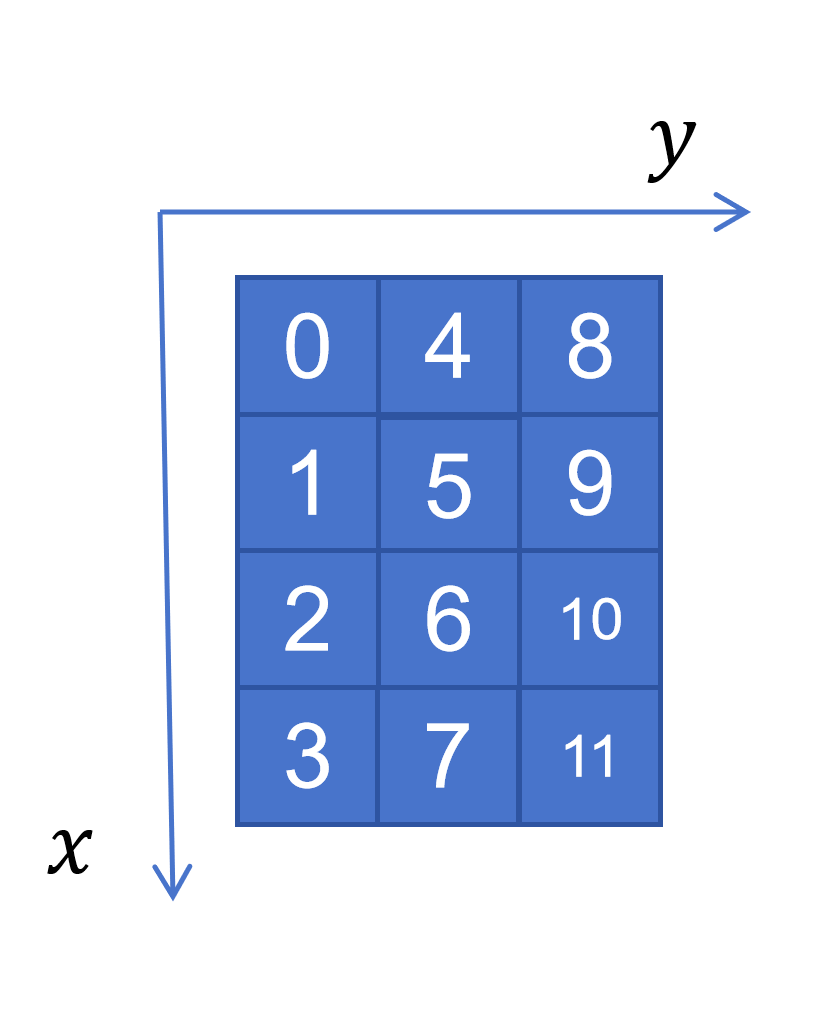
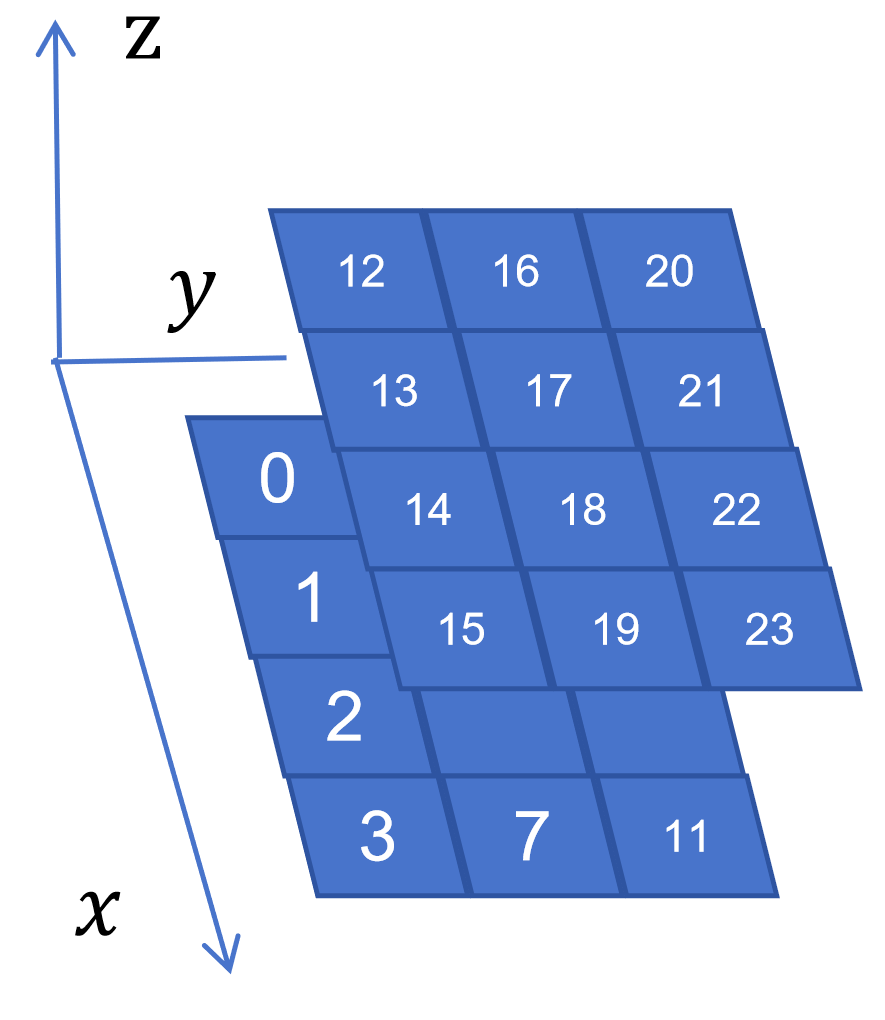
那么我们需要遍历mesh中的每一个点,找到对应的cell并且加入其中,以便我们对于每一个cell做生成新顶点的处理。至此,原数据中的mesh所有点的数据,都加入到了对应的cell中,接下来就是对于cell的处理。
int getCellIndex(const BoundaryBox& bbox, const Vertex& v, int nx, int ny, int nz) {
// 计算每个方向的单元格大小
double dx = bbox.lenX / nx;
double dy = bbox.lenY / ny;
double dz = bbox.lenZ / nz;
// 计算单元格索引,使用 std::floor 确保正确分配
int ix = static_cast<int>(std::floor((v.x - bbox.minX) / dx));
int iy = static_cast<int>(std::floor((v.y - bbox.minY) / dy));
int iz = static_cast<int>(std::floor((v.z - bbox.minZ) / dz));
// 处理边界情况,确保索引在 [0, n-1] 范围内
ix = std::min(std::max(ix, 0), nx - 1);
iy = std::min(std::max(iy, 0), ny - 1);
iz = std::min(std::max(iz, 0), nz - 1);
// 计算最终的单元格编号
int index = iz * nx * ny + iy * nx + ix;
// if (v.z bbox.maxZ) {debug3(ix, iy, iz); debug(index); }
return index;
}
int main() {
// ...
std::vector<std::vector<int>> cells(m);
for (int i = 0; i < n; i++) {
int idx = getCellIndex(mesh.bbox, mesh.vertices[i], nx, ny, nz);
// 找到对于点i的cell编号
assert(idx >= 0 && idx < m); // 检测是否有越界情况
cells[idx].push_back(i); // 第idx个编号的cell加入第i点
}
// ...
}2.3.2 生成新顶点
顶点聚类需要我们对于每一个cell进行生成新顶点的处理,常见的方法有平均值方法和中值方法,也有二次误差度量(QEM),这个并未在此展示。
方法一:顶点位置的平均值
在本方法中,新顶点的位置是通过计算顶点集群中所有顶点坐标的平均值来确定的。具体步骤如下:
- 对每个顶点集群中的所有顶点坐标求和。
- 将求和结果除以顶点数量,得到平均值。
- 将平均值作为新顶点的位置。
Vertex getNewVertexAve(const std::vector<int>& vec, const Mesh& mesh) {
float newX = 0, newY = 0, newZ = 0;
Vertex newVertex;
for (auto &v: vec) {
newX = mesh.vertices[v].x;
newY = mesh.vertices[v].y;
newZ = mesh.vertices[v].z;
} // 加和
newVertex.x = newX / vec.size();
newVertex.y = newY / vec.size();
newVertex.z = newZ / vec.size(); // 求平均
return newVertex;
}方法二:顶点位置的中值
在本方法中,新顶点的位置是通过计算顶点集群中所有顶点坐标的中位数来确定的,可以避免边缘极端情况。具体步骤如下:
- 对每个顶点集群中的所有顶点坐标的
x,y,z分别加入至对应列表中。 - 对每一个列表进行排序取中值。
- 将三个列表的中值作为新顶点的位置。
Vertex getNewVertexMid(const std::vector<int>& vec, const Mesh& mesh) {
std::vector<float> xVals, yVals, zVals;
Vertex newVertex;
for (auto &v : vec) {
xVals.push_back(mesh.vertices[v].x);
yVals.push_back(mesh.vertices[v].y);
zVals.push_back(mesh.vertices[v].z);
} // 分别加入三个列表中
// 排序并计算中位数
std::nth_element(xVals.begin(), xVals.begin() + xVals.size() / 2, xVals.end());
std::nth_element(yVals.begin(), yVals.begin() + yVals.size() / 2, yVals.end());
std::nth_element(zVals.begin(), zVals.begin() + zVals.size() / 2, zVals.end());
newVertex.x = xVals[xVals.size() / 2];
newVertex.y = yVals[yVals.size() / 2];
newVertex.z = zVals[zVals.size() / 2];
return newVertex;
}值得注意的是,对于每一个cell遍历的时候,需要忽略不含有任何一个点的cell,当然并不是每一个划分都一定有点在其中的,不需要调用上述函数。并且在最后需要“清除”,以便我们生成完整的数据,在映射的时候也同样需要注意。
2.3.3 生成新拓扑关系
如图2-1所示,我们需要在生成新顶点之后,需要按照原来的拓扑关系(面)生成新的面。首先需要遍历原数据的每一个面,然后判断是否有任意两个点在同一个cell中,如果是则无需考虑,因为三个点其中有两个点是同一个新顶点的话,那么此时二维的面将变成了一维的线。
此时的新顶点的编号就是对应的cell编号,那么此时在不同的面中的点就可以生成新的面,而面的点信息就是cell的编号。只需要将这些cell的编号加入至一个新的面(Face newFace)中即可,最后将所有的面信息统计起来就是新的数据信息了。
在这里我使用的是集合std::set来统计cell的编号,如果集合的数量不小于原来面中点的数量,那么就是符合都在不同cell的情况,需要统计起来处理。
for (int i = 0; i < f; i++) {
auto &face = mesh.faces[i];
std::set<int> s;
for (auto &v: face.vertexIndices) {
int idx = getCellIndex(mesh.bbox, mesh.vertices[v], nx, ny, nz);
assert(idx >= 0 && idx < m);
s.insert(idx); // 将点的下标存储至s中
}
if (s.size() >= face.vertexIndices.size()) { // 都处于不同cell
Face newFace;
for (auto &idx: s) {
newFace.vertexIndices.push_back(idx);
}
newFaces.push_back(newFace);
}
}2.3.4 清洗数据
至此,我们已经完成了新数据的生成,让我们来看看现在拥有什么。我们有一个std::vector<Face> newFaces,这里保存了所有面,每一个面里面拥有的是对应cell的下标。但是这个的下标并不是连续的,需要做离散化的处理,如图2-3.
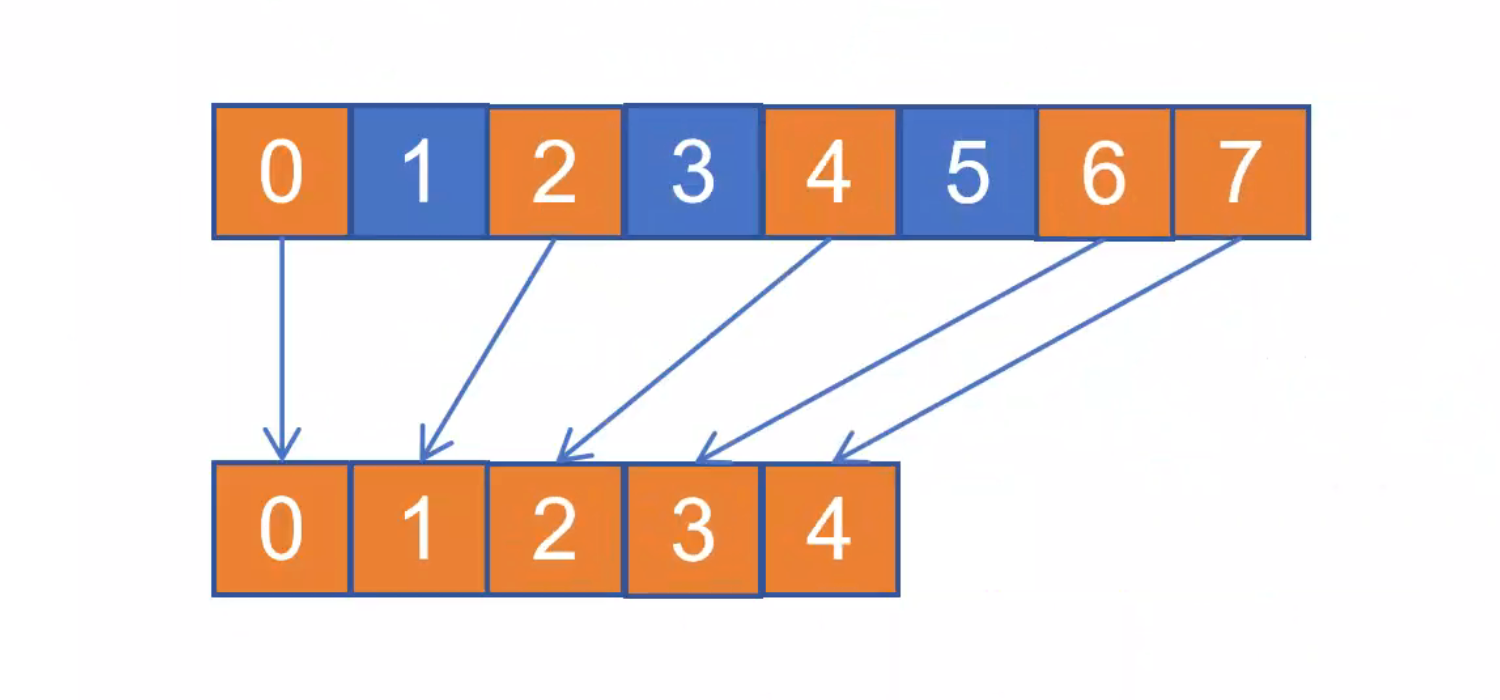
做离散化操作的方法有很多种,我在这里使用的是std::map作映射,遍历所有的cell如果为非空则计数加一,这样就可以达到离散化的效果。这样我们就得到了一个映射关系,而在newFaces中存放的是cell的编号,输出的时候只需要调用这个映射即可。
int cnt = 0;
std::map<int, int> mp;
for (int i = 0; i < m; i++) {
if (cells[i].size() 0) continue;
mp[i] = cnt++;
}2.4 文件输出
至此,只需要将在2.3.2和2.3.3中的newVertices和newFaces进行输出至对应文件位置即可,需要注意的是OFF文件的格式,然后再输newVertices每个点的三维坐标和newFaces经过映射后的点的编号。
std::ofstream outfile("output.off");
outfile << "OFF" << std::endl;
outfile << cnt << " " << newFaces.size() << " 0" << std::endl;
for (int i = 0; i < m; i++) {
if (cells[i].size() 0) continue;
auto &v = newVertices[i];
outfile << v.x << " " << v.y << " " << v.z << std::endl;
}
for (auto &face: newFaces) {
outfile << face.vertexIndices.size();
for (auto &v: face.vertexIndices) {
outfile << " " << mp[v];
}
outfile << std::endl;
}
outfile.close();2.5 豪斯多夫距离
豪斯多夫距离(Hausdorff Distance)是一种度量空间中两个集合相似度的方法,广泛应用于计算几何、模式识别、图像处理等领域。它通过考虑集合之间的最远距离来衡量两个集合的差异,尤其适用于点集或形状比较的情形。在本次实验中,我们也会用此距离进行定量的计算并且分析。
给定两个非空的点集 ( A ) 和 ( B )(通常为拓扑空间中的子集),豪斯多夫距离 ( d_H(A, B) ) 定义为:
d_H(A, B) = \max \left( \sup_{a \in A} \inf_{b \in B} \| a - b \|, \sup_{b \in B} \inf_{a \in A} \| b - a \| \right)
其中:
| a - b \|表示点a和点b之间的距离,通常采用欧几里得距离;\inf_{b \in B} \| a - b \|表示集合B中到点a最近的点的距离;\sup_{a \in A} \inf_{b \in B} \| a - b \|表示集合A中所有点到集合B最近点的距离的最大值;\sup_{b \in B} \inf_{a \in A} \| b - a \|表示集合B中所有点到集合A最近点的距离的最大值。
豪斯多夫距离考虑了两个集合之间的最远距离,即它不仅考虑集合内的每个点到另一集合中最接近点的距离,还考虑了反向的距离。因此,豪斯多夫距离可以有效衡量集合之间的差异,特别适合于形状匹配和点集比较的应用。代码如下,
// 计算豪斯多夫距离(近似,使用顶点到顶点的距离)
float computeHausdorffDistance(const Mesh& mesh1, const Mesh& mesh2) {
float hausdorff = 0.0f;
// 从mesh1到mesh2
for (const auto& v1 : mesh1.vertices) {
float minDist = std::numeric_limits<float>::max(); // 初始化最大值
for (const auto& v2 : mesh2.vertices) {
float dist = distance(v1, v2);
if (dist < minDist) {
minDist = dist;
if (minDist 0.0f) break; // 最小距离
}
}
if (minDist > hausdorff) {
hausdorff = minDist;
}
}
// 从mesh2到mesh1
for (const auto& v2 : mesh2.vertices) {
float minDist = std::numeric_limits<float>::max(); // 初始化最大值
for (const auto& v1 : mesh1.vertices) {
float dist = distance(v2, v1);
if (dist < minDist) {
minDist = dist;
if (minDist 0.0f) break; // 最小距离
}
}
if (minDist > hausdorff) {
hausdorff = minDist;
}
}
return hausdorff;
}三、实验结果
本次进行实验的数据来自于PUNet数据集。

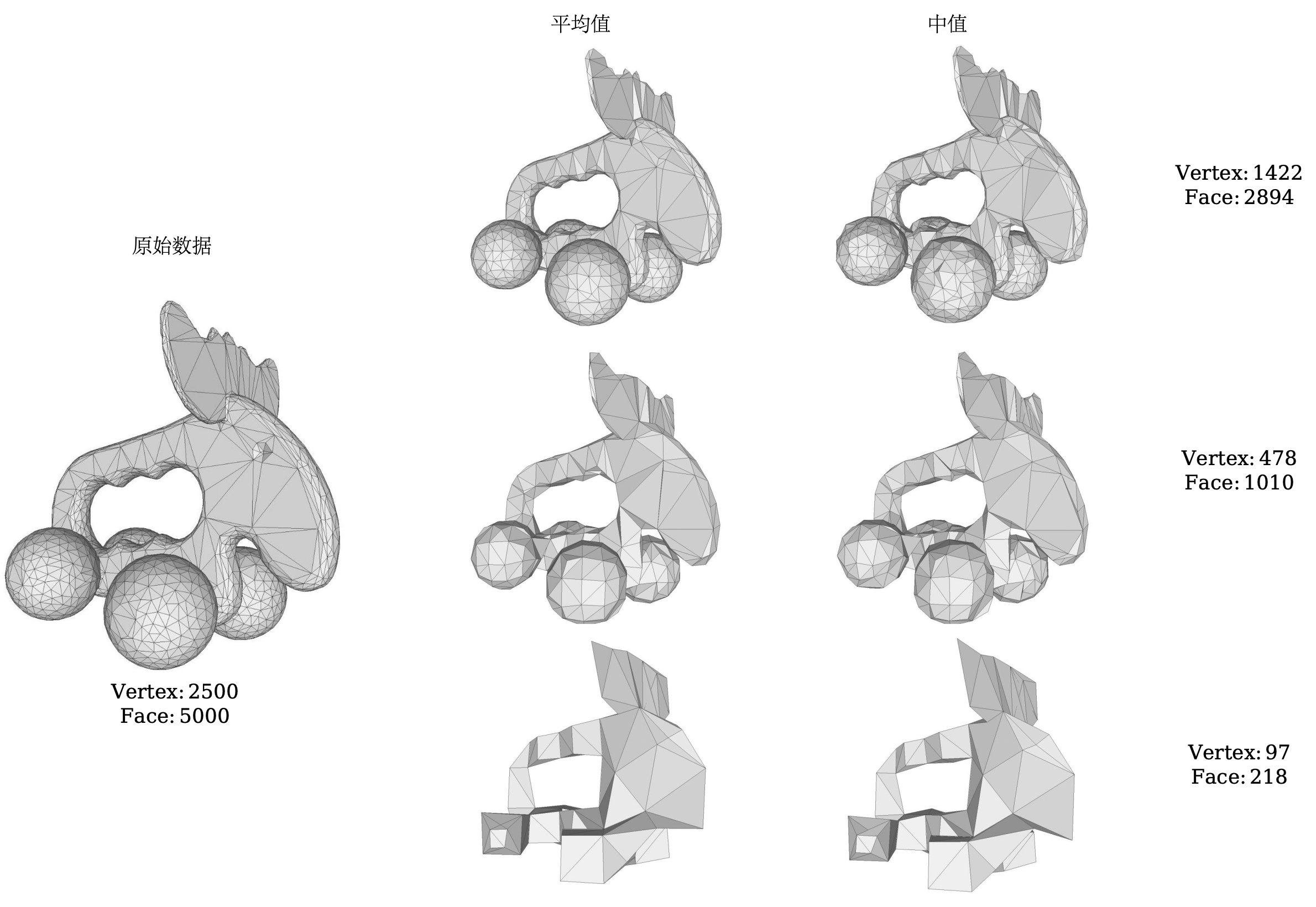
我选取数据集中单独展示的是训练集中的elk.off,我们对其进行两种方法的三种网格简化程度的形式进行简化,得到的结果如图3-1。原数据一共2500个点,5000个面,显示在图的左侧,通过构建关系可以得出三种网格简化程度,数据都是三角面片,结果分别为:
- 中等简化:
1422点,2894个面 - 高程度简化:
478点,1010个面 - 极简化:
97点,218个面
3.1 纵向分析:同种方法不同简化程度之间的关系
我们依次从上往下看,每次简化都能够得到完整图形,大体上还是保持类似的形状以及拓扑结构,中等简化表现出顶点聚类的网格分析的好处,而高程度简化也能够表达出一些特征,只不过极简化情况下由于点面信息太少导致过于锐利,不够平滑。
首先来看中等简化情况下,两种方法都保持了大致的特征,例如在麋鹿的角以及头部都能明显看出,而对于四个球也能够明显表达。 从背部等处几何形状细节仍然较好,边缘轮廓光滑且完整。
再来观察高程度简化情况下,大致上还是可以看出麋鹿角、头部、背部以及四个球的轮廓,但是仔细发现背部镂空的两个凸起已经逐渐平滑,而且头角处也成为了一条曲线。总而言之,球体还保持大致的形状,但细节之处已经不足以保留下来。
最后来看极简化下,我们以及无法能够得出它是一只麋鹿了,四个球也成为了类似于长方体的形状,毫无光滑之言,而头角处更是接近一个面。在这种程度之下并不能保留信息,因为其保存的信息过于稀少。
尽管这样,也足以说明本次实验的成功,因为顶点聚类就是在保留特征和代价之间进行平衡,当数据过于少的时候那么当然不能保存原来的种种信息,所以这是在追求一种平衡。
3.2 横向分析:不同种方法同简化程度之间的关系}
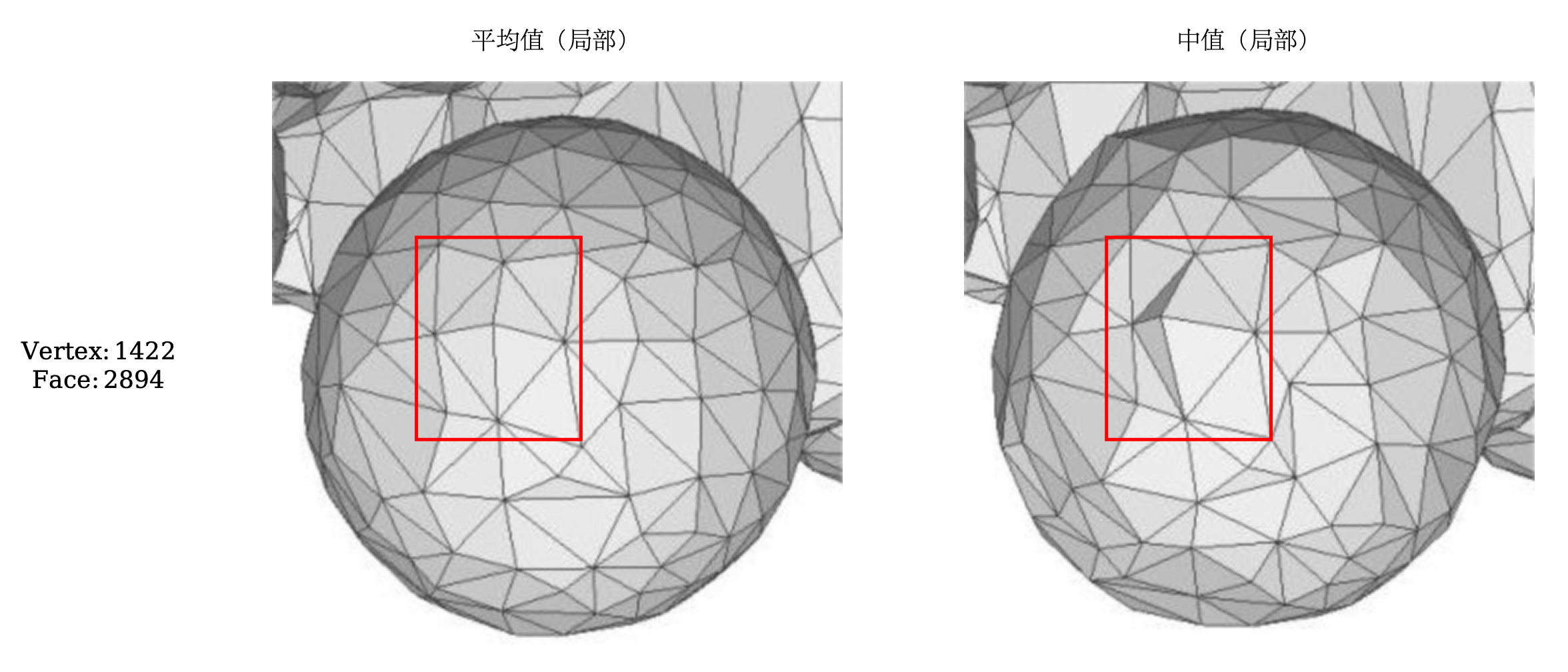
尽管二者在简化方面表现的优秀,但是在细节方面中值方法表现不佳。从图3-2的红色框选区域可以看出,平均值方法在处理光滑表面时,能够更好地保持整体的曲面形态,其表面更加平滑自然,几何结构呈现出一定的连续性。这种表现是由于平均值方法在光滑区域中对各顶点的位置进行了合理的平滑调整,有效地减少了可能存在的局部突兀情况。然而,与之对比的中值方法在相同区域中未能很好地体现曲面的连续性,部分网格显得生硬,甚至可能引入新的几何异常。这种现象主要归因于中值方法倾向于去除局部噪声,而忽略了在光滑区域保持几何连续性的重要性。
因此,如果是在光滑的表面,我们往往选择平均值方法会更加优秀,而在具有很大噪声的情况下,我们选择中值的方法会更加优秀。
3.3 整体分析:使用豪斯多夫距离进行分析
我们同样选取elk.off文件进行三种模式的网格简化,经过两种不同的方法得到的数据与原来数据进行测量豪斯多夫距离,结果如表3-1。其中原始数据并未做任何处理,豪斯多夫距离为0。
| 数据类型 | 平均值方法距离 | 中值方法距离 | 点比例 | 面比例 |
|---|---|---|---|---|
| 原始数据(2500点,5000面) | 0 | 0 | 100% | 100% |
| 中等简化(1422点,2894面) | 0.0383828 | 0.0477667 | 56.88% | 57.88% |
| 高简化(478点,1010面) | 0.0911515 | 0.0945222 | 19.12% | 20.20% |
| 极简化(97点,218面) | 0.184343 | 0.184377 | 3.88% | 4.36% |
我们可以发现,随着简化程度的增加,豪斯多夫距离越来越大,这也就表明我们在简化了网格的同时也损失了一定的特征,这就是所说的代价。可以看到中等简化保留了原来56.88\%的点以及57.88\%的面信息,两种方法的距离仅在0.4左右,而极简化的时候仅只有原来的3.88\%的点以及4.36\%的面的信息,距离则超过了0.18,通过图形也可以发现损失了很多的信息。
从横向两种方法对比来看,在中等简化的时候二者相差较大,而程度越高时距离相差较小,数值接近。所以从这个角度来看,我们对中等简化情况下进行分析,从图形的方面上看确实是中值方法表现不如平均值的方法,因为我们的数据比较规整,并没有多少的噪声,而平均值方法更能表现其优点。
3.4 其他数据分析
在这里,我们进行一些其他数据进行可视化,我挑选了鸭和牛进行可视化,即duck.off和cow.off数据。
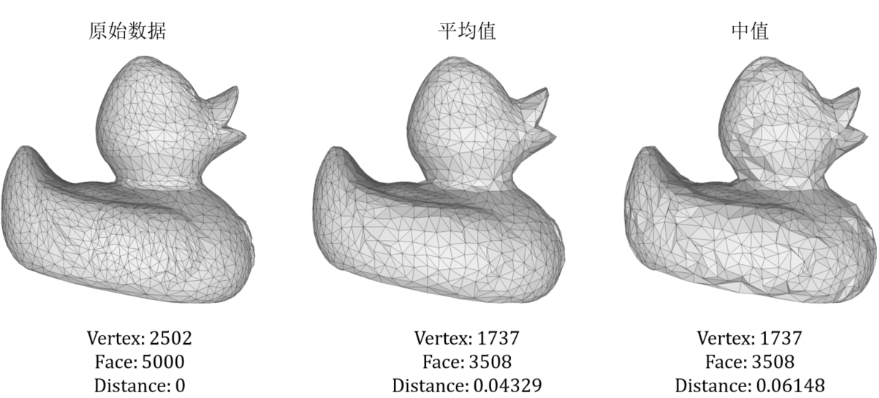
我们首先来对duck.off数据用中等程度的网格简化以及原始数据进行可视化,结果如图3-3所示。我们可以看到原始数据为2502个点和5000个面,而中等程度后数据为1737个点和3508个面。平均值方法和中值方法得到的结果总体上表现的还不错,可以正确识别尾部、身体以及包括鸭嘴在内的头部,但是豪斯多夫距离差别较大,分别为0.04329和0.06148,平均值方法表现更加,从尾部来看更加平滑,而中值方法则在尾部拥有了凸起的形变。不仅如此,在头部也有这样的效果,这也说明了确实在平滑的地方平均值更能表现局部的特征,表现更加。
我选取了拥有更多点面数据的cow.off进行同样的测试,并且选取了多角度进行分析,如图3-4所示。原始数据一共有4315个点和8626个面,而中等程度简化成2352个点和4974个面
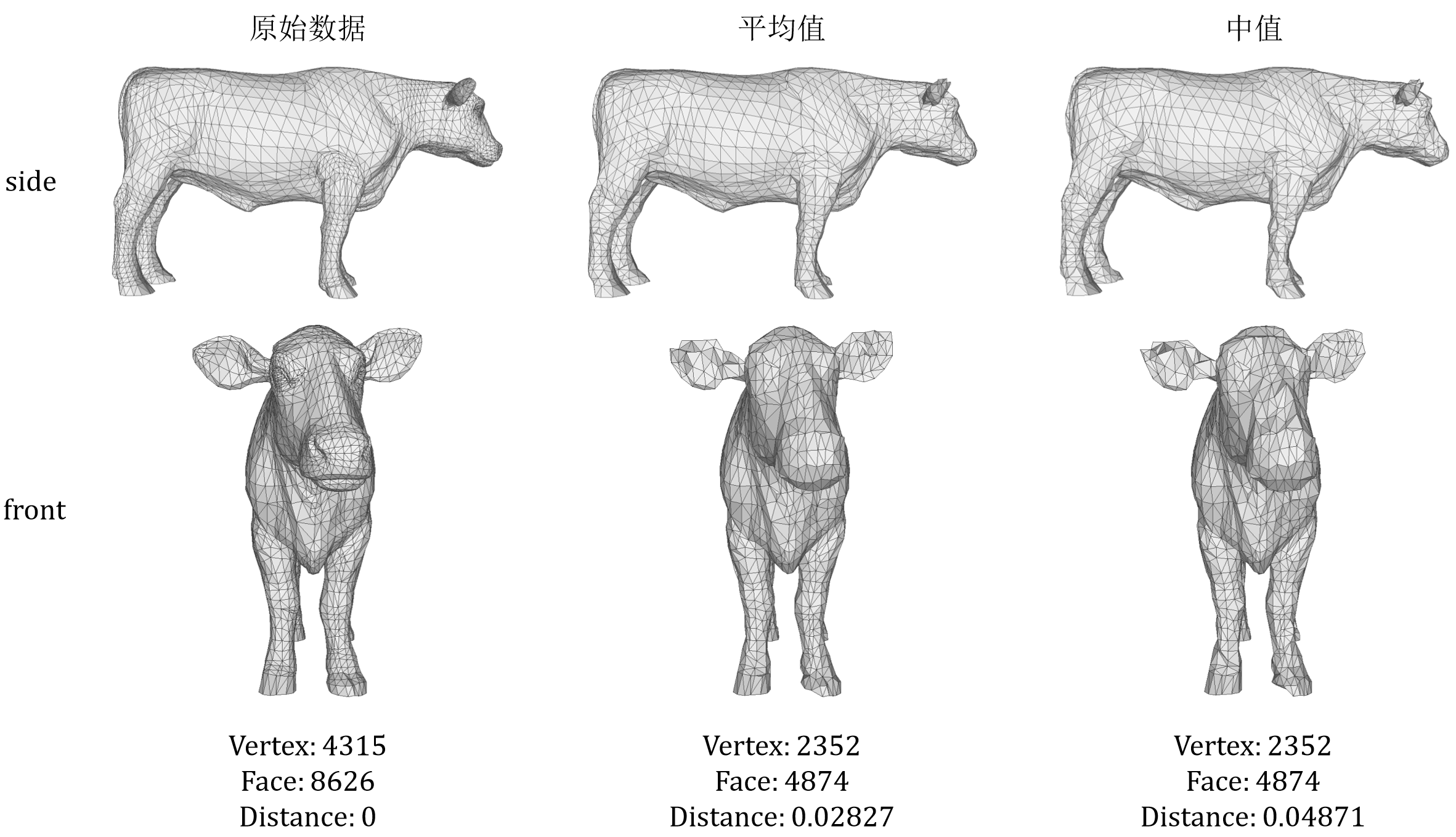
从整体上来看,侧边表现良好,可以正确识别四肢以及身体,而腹部的凸起也较好的表现出来,头部嘴和耳朵的特征也能够良好的保存。但从正面查看细节却表现不佳,从耳朵来看两种方法已经严重变形,最严重的当属眼睛之处,在两种方法上已经毫无眼睛信息可言。这是因为原数据中眼睛处拥有较密集的点面信息,但是经过顶点聚类的方法会导致均匀浓缩至一部分点,这不符合常理,所以导致了严重的变形。在左前方的脚处也能明显感觉到中值方法保留的锐利的特征,而平均值的方法稍微好一些。
二者方法比较而言,还是平均值方法的豪斯多夫距离远远小于中值方法的举例,分别是0.02827和0.04871。而从可视化图的角度而言也确实中值方法表现不佳。
四、总结与思考
4.1 总结
本次实验主要完成了基于顶点聚类的网格简化处理,并且使用了平均值方法和顶点方法来选取生成新顶点。在实验中,我们有定性的分析也有定量的计算,通过可视化图的细节特征和使用豪斯多夫距离相比较进而进行分析与探讨,得出了一些结论与总结如下:
- 总体而言实验表现良好,算法成功实现。
- 平均值方法在处理光滑之处更加良好,而中值方法在处理噪声的部分表现更好。
- 随着简化程度的增加,保留的信息也越来越少。
- 在定量计算的时候,我们可以采用豪斯多夫距离距离或者倒角距离和
P2M距离。
4.2 思考
思考一:结合二者方法
既然平均值方法和中值方法各有利弊,是否可以将二者进行结合?在光滑的地方多使用平均值方法,在噪声多的地方多使用中值方法。或者赋予二者一个权重进行加权平均值,这涉及到更多的步骤。
思考二:对于网格疏密的思考
从图3-4可以发现,在细节较多即网格较密的地方顶点聚类方法表现不佳,因为都处于同一个cell那么就会聚成一个点。因为每一个cell的大小形状都是一样的,那么哪怕再多的信息在其中都无济于事,我们是否可以调整cell的大小呢?从直觉上而言,当细节多的地方就应该保留更多的特征,那么此时不应该都汇聚成一个点,而细节少的地方则无须过多地调整。
思考三:使用基于二次度量误差的网格简化方法
可以采用二次度量误差的方法(QEM)进行处理网格简化,基本的思想就是不断地收缩边,直到达到我们所需要的三角形数量,我们收缩的边越多,网格越简单。
