MarchingCube
一、简介
MarchingCube是一种图形学算法,发表于SIGGRAPH198。用于从三维离散标量场(或体素)中提取等值面的多边形网格(Mesh)。
换句话说,我知道一个标量场和一个等值 iso-value 我就可以得到一个Mesh出来。注意这并不是从点云到Mesh的算法,还需要进行一定的操作,例如表面重建成Mesh。
二、算法
2.1 二维图形的栅格化
首先来看二维图像的栅格化是什么样的,首先要表示如下的图片

最简单的方式就是栅格化

我们对于顶点进行着色,在图形内的就是红色🔴,在图形外的就是🔵
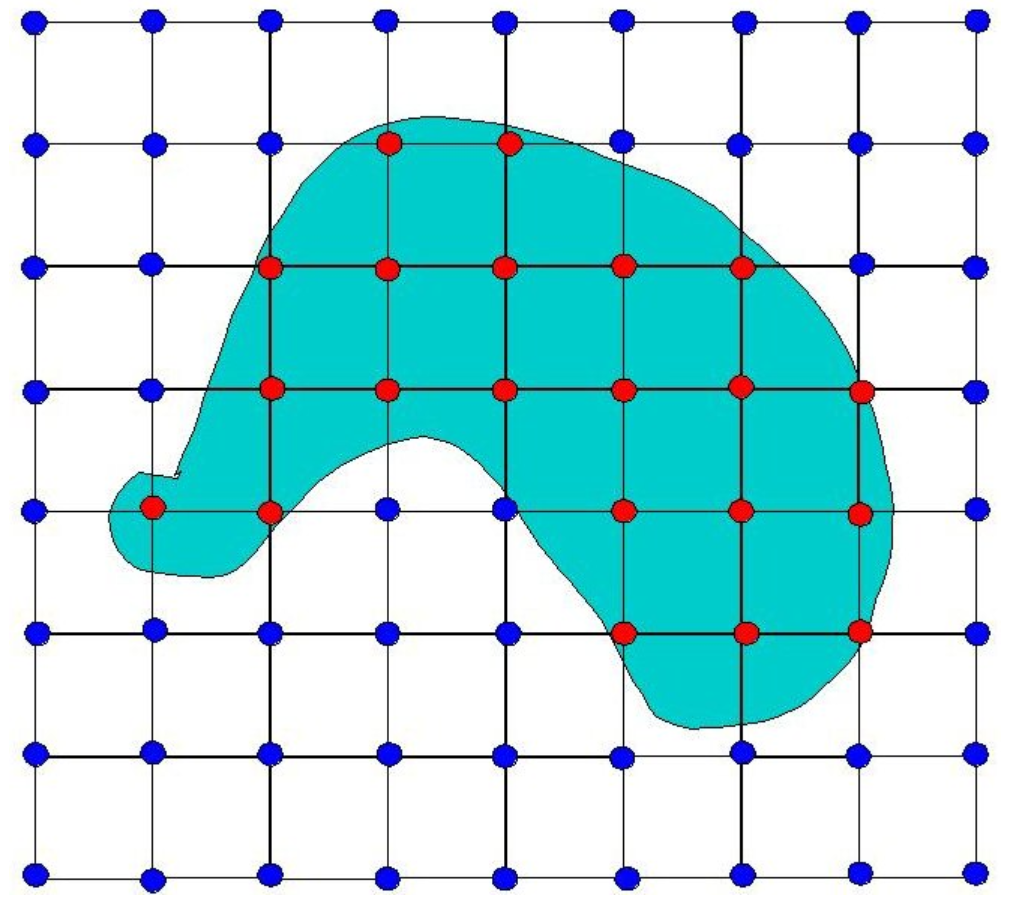
但是直接这样来表示十分丑陋(不准确),我们这里取红色🔴和蓝色🔵的中点为粉色
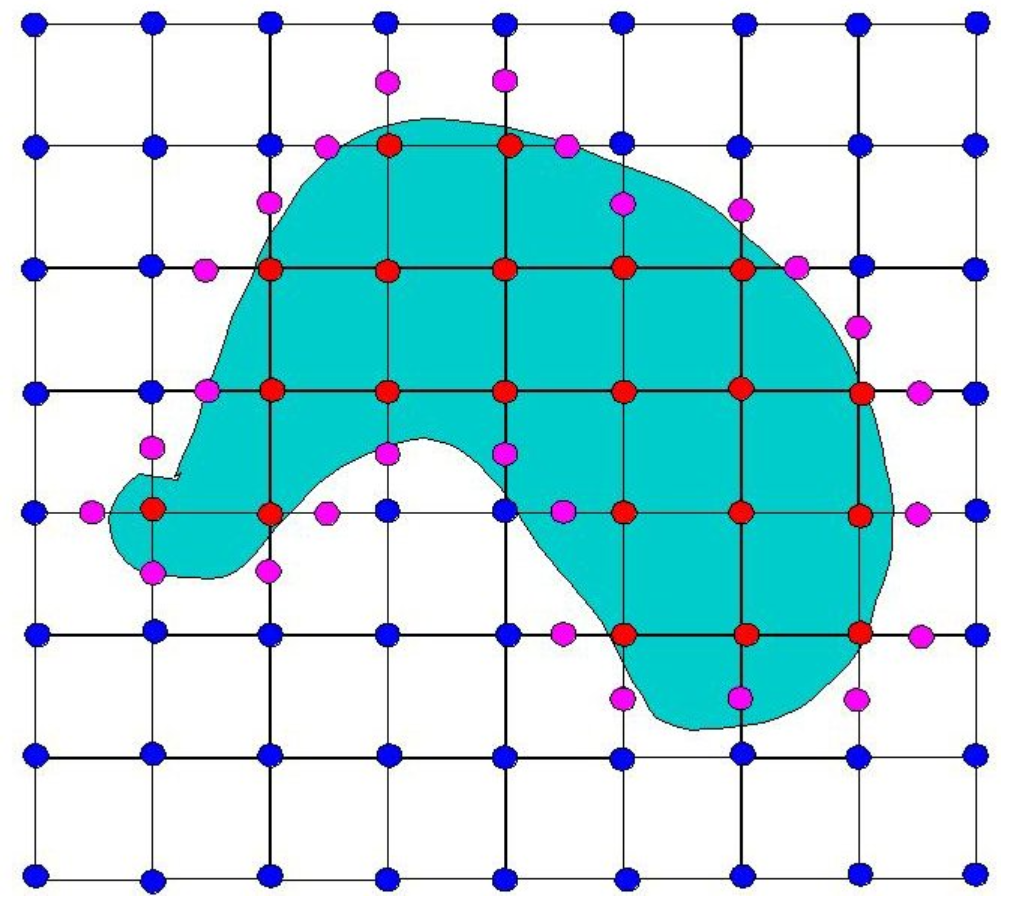
这个是时候就可以得到与原来相似的图形了(但还可以优化)
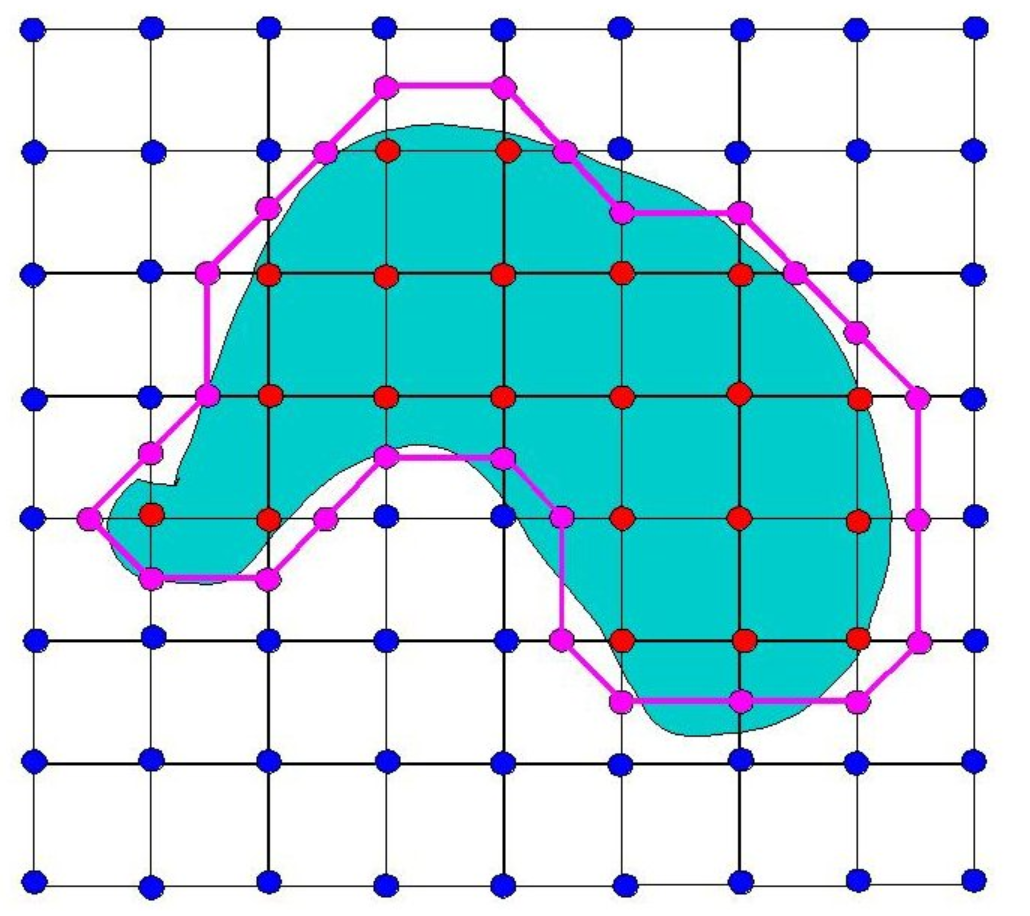
2.2 三维图形的栅格化
三维的物体也是一样的道理,二维里面是正方形,那么三维里面就是正方体(Cube),同样对于一个正方体来说,八个顶点也需要按照上面的方法进行染色,在图形内部的就是红色🔴,在图形外部的就是蓝色🔵,每一个红色🔴和蓝色🔵之间就要生成一个粉色
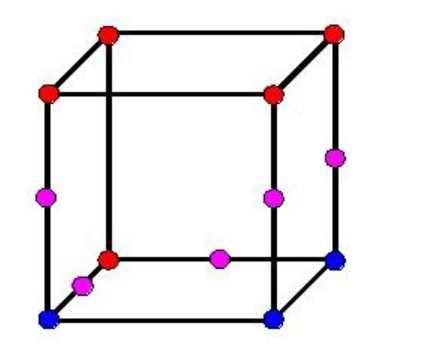
那么现在要把粉色的点连接起来,连接起来应该怎么连呢?我随手画了以下三种:
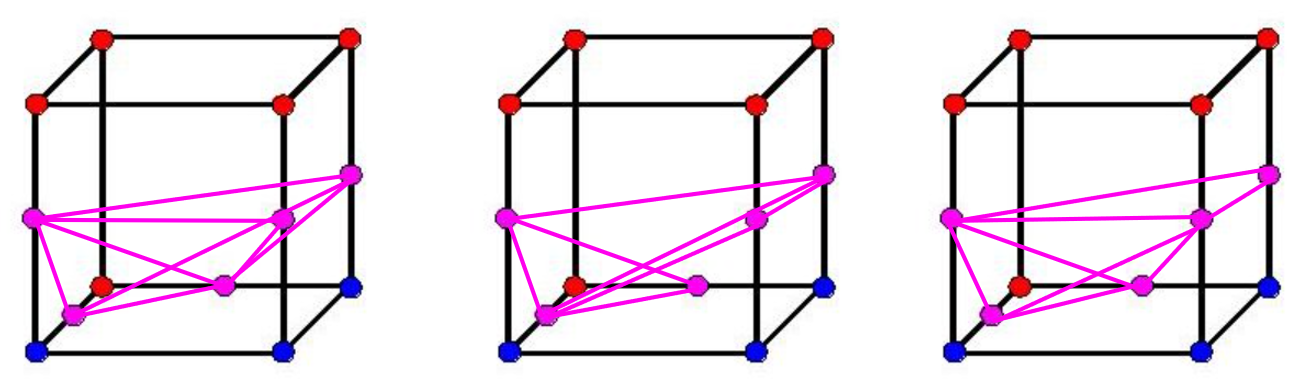
当然是不合理的(看起来就是),那么我们来具体分析一下。
一个cube有8个顶点,每个顶点有红🔴、蓝🔵两种选择,那么就一共有2^8=256中情况,考虑到旋转和镜像都是一种情况,只剩下了15种:
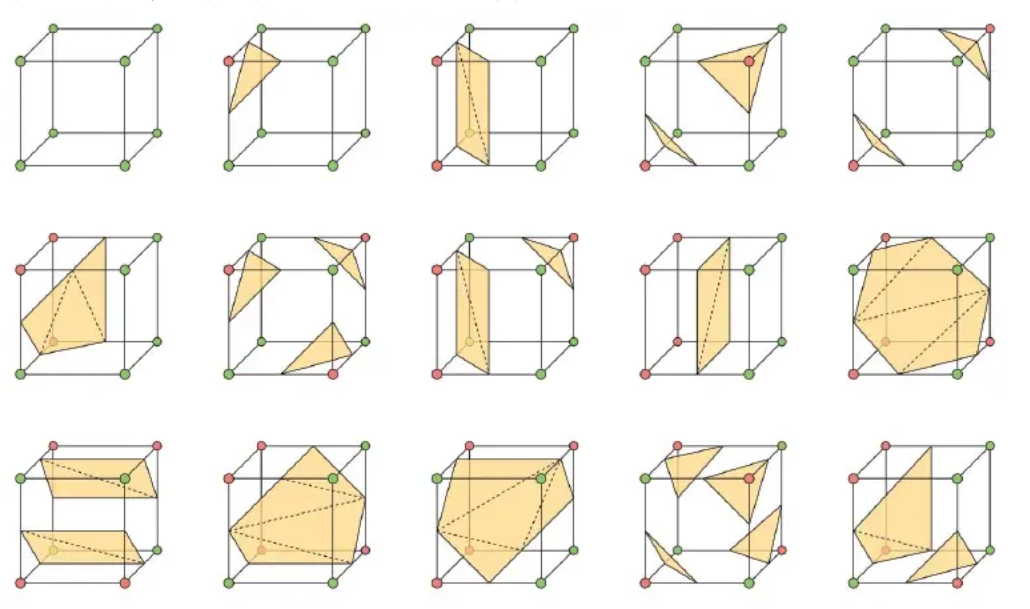
那么对于所有的256种情况我可以用一个8 \text{bit}的数来表示,那么此时可以用hash表来表示每一种情况对应哪样的组合,例如
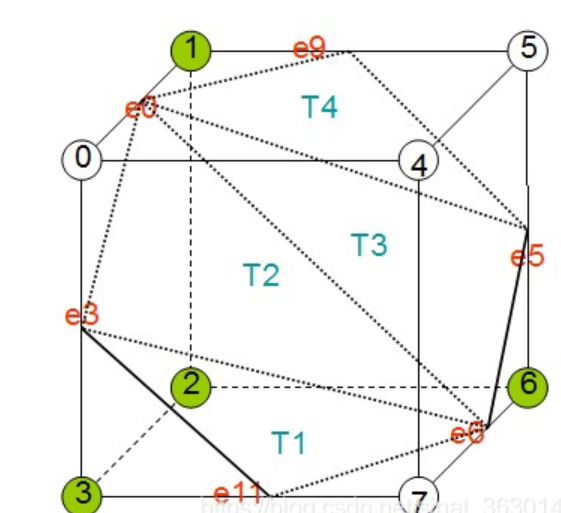
这张图表示1、2、3、6号点在图形的内部,其余点在外部,我们将不同颜色的中点选取出来也就是上面的e,有e0,e3,e5,e6,e9,e11,对应上面十五种那种情况呢?也就是第二排最右边那个。
其实不需要这么看,只需要看1,2,3,6就可以找出来正好是第二排最右边那个,那么此时我们直接构建三角形即可。
hash表中如下:
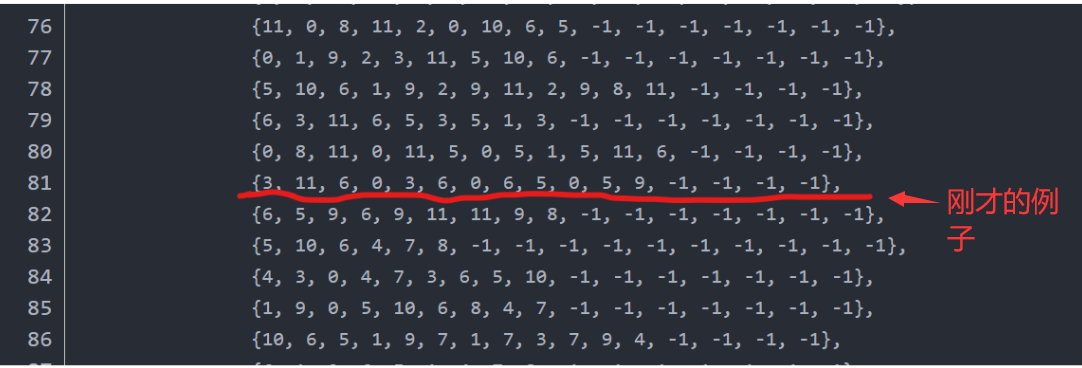
我们看到这个hash表一共有256行,16列。因为顶点的颜色组合有256种,所以有256行。而每一行中每3个数表示一个三角形,而一个cube中最多的情况有5个三角形,所以需要15个数, 再加一个-1表示结尾,所以一共有16列。
这一行
{3, 11, 6, 0, 3, 6, 0, 6, 5, 0, 5, 9, -1, -1, -1, -1}表示什么意思呢?
每三个数表示一个三角形面片,例如前面的3, 11, 6则表示的是e_3,e_{11},e_6,这种情况一共四个三角形,所以后面四个是-1
2.3 Smooth平滑
正如之前所说,直接取中点表现还不佳,那么我们可以使用插值算法,变化如下:
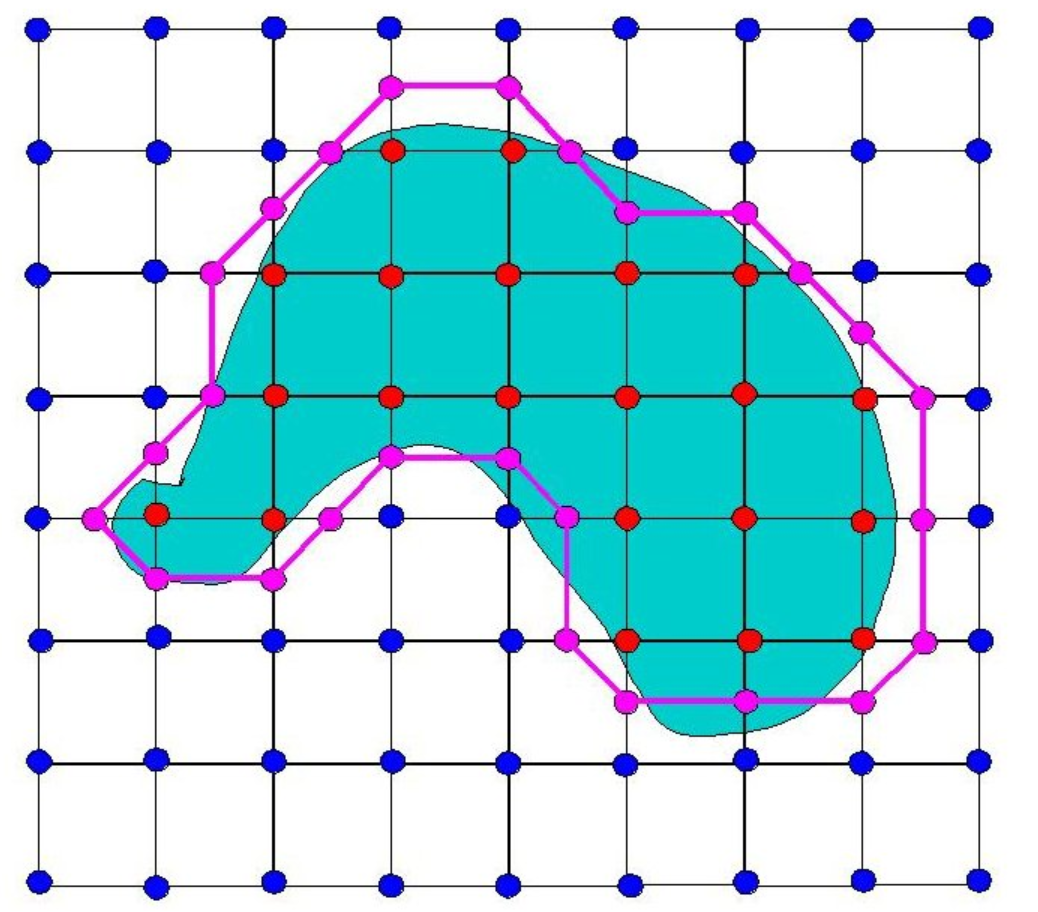
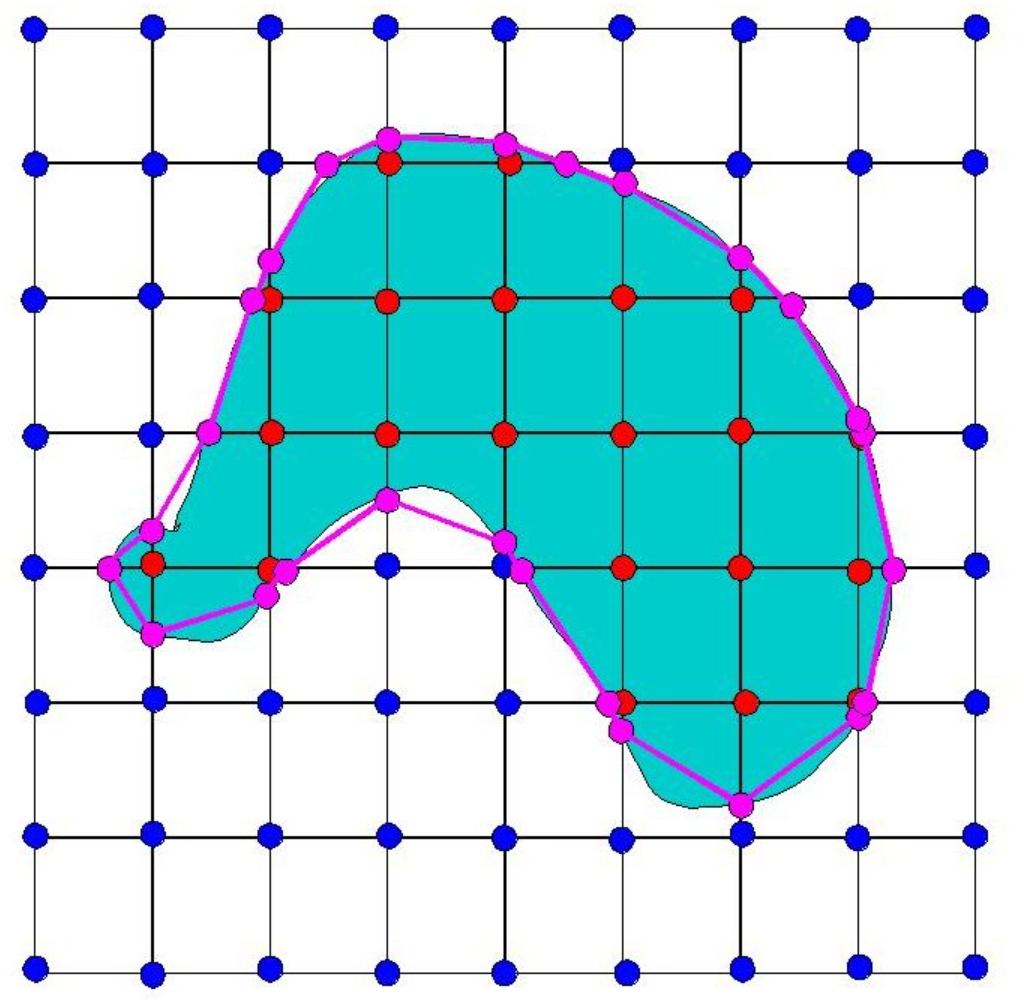
这样的操作之后可以表现得更好,得到较为平滑的结果。

Smooth之后:

三、展示
展示一下我现在的结果:


