Games101作业2

2024年12月5日 下午4:27 计算机图形学 ,

Games101作业2

image-20241205162402901

一、任务

需要自己填写rasterize_triangle(const Triangle& t)函数

该函数的内部工作流程如下：

  1. 创建三角形的2维bounding box。
  2. 遍历此 bounding box 内的所有像素（使用其整数索引）。然后，使用像素中心的屏幕空间坐标来检查中心点是否在三角形内。
  3. 如果在内部，则将其位置处的插值深度值 (interpolated depth value) 与深度缓冲区 (depth buffer) 中的相应值进行比较。
  4. 如果当前点更靠近相机，请设置像素颜色并更新深度缓冲区 (depth buffer)

你需要修改的函数如下：

  • rasterize_triangle(): 执行三角形栅格化算法
  • static bool insideTriangle(): 测试点是否在三角形内。你可以修改此函数的定义，这意味着，你可以按照自己的方式更新返回类型或函数参数。

已知的是三角形三个顶点处的深度值，每一个三角形的颜色都是一样的。那么需要用插值的方法获得深度值。

二、作业

2.0 完成其他函数的编写

首先需要完成main.cpp中的get_projection_matrix()函数的编写，直接复制前一个作业的函数

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
    // TODO: Copy-paste your implementation from the previous assignment.
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f Mperspective;
    Mperspective << zNear, 0, 0, 0,
        0, zNear, 0, 0,
        0, 0, zNear + zFar, -zNear * zFar,
        0, 0, 1, 0;

    float half_height = std::tan(eye_fov / 2) * -zNear;
    float half_width = half_height * aspect_ratio;

    Eigen::Matrix4f Morth;
    Morth << 1 / half_width, 0, 0, 0,
        0, 1 / half_height, 0, 0,
        0, 0, 2 / (zNear - zFar), (zFar - zNear) / (zNear - zFar),
        0, 0, 0, 1;

    projection =   Morth * Mperspective;
    return projection;
}

然后完成判断点(x,y)是否在三角形内的函数insideTriangle()，主要采用的是对于每一条边都进行叉乘，判断是否都是竖直向上的（右手定则）

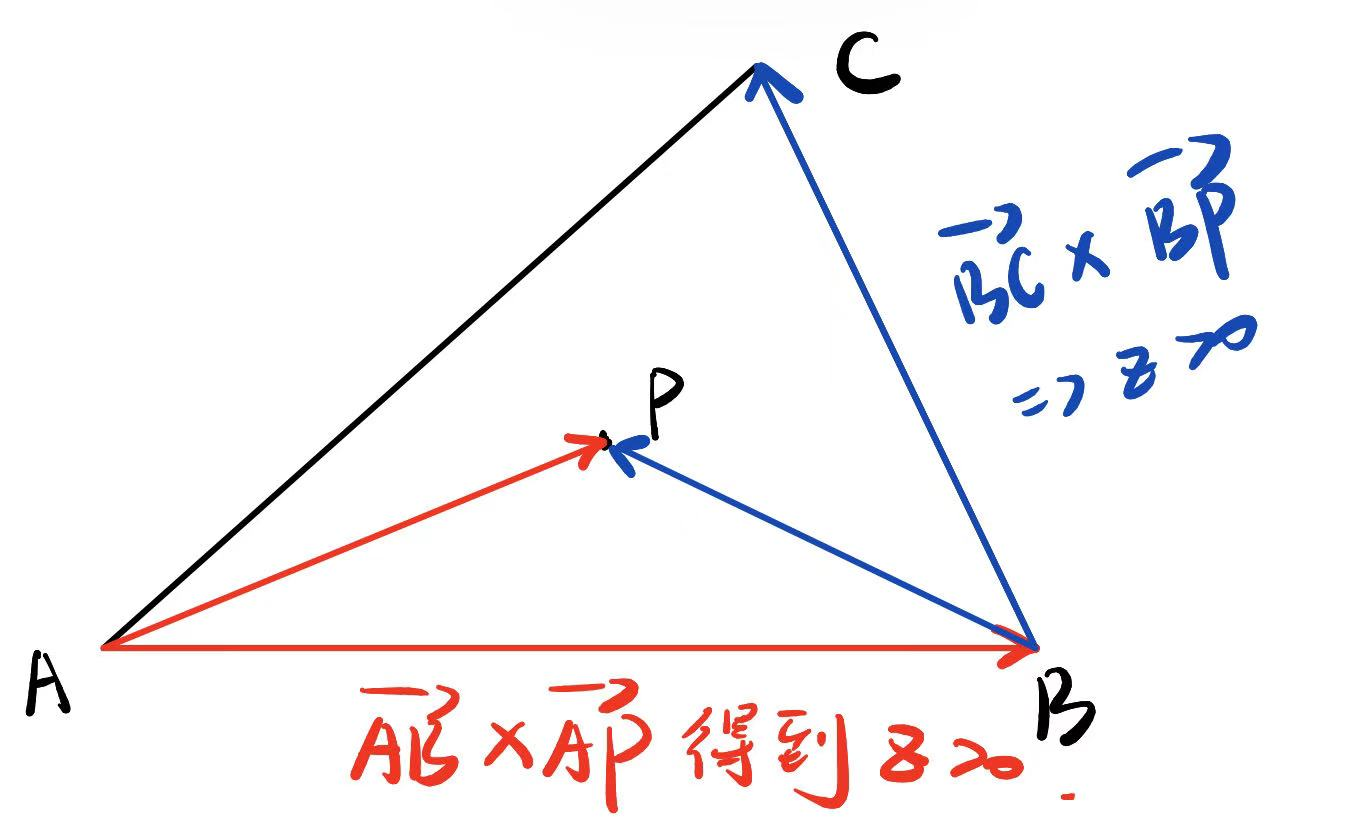
image-20241205154243026 
static bool insideTriangle(float x, float y, const Vector3f* _v) // float
{   
    // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
    Vector3f A = _v[0], B = _v[1], C = _v[2];
    Vector3f P(x, y, 0);
    Vector3f AB = B - A, BC = C - B, CA = A - C;
    Vector3f AP = P - A, BP = P - B, CP = P - C;
    return AB.cross(AP).z() > 0 && BC.cross(BP).z() > 0 && CA.cross(CP).z() > 0;
    // cross表示的是叉乘，z()表示的是z坐标
}

至此其他函数全部结束，主要完成rasterize_triangle()函数的编写

2.1 不带MSAA的光栅化

给出一个三角形的三个点的坐标信息，则需要对于光栅化中每一个像素进行判断，对于(x,y)像素应该是什么颜色的\mathbf{color}。首先为了节省不必要的浪费，需要求bounding box，在这里面进行判断即可，求出minx,maxx,miny,maxy四个变量。

接着对于每一个像素进行遍历，因为这个函数传入的是当前的三角形，而深度测试的变量则是一个类似于全局变量的东西，所以需要对于当前三角形bounding box中每一个像素进行判断：

  1. 像素(x,y)是否在三角形内？不在直接不进行任何考虑
  2. 在三角形内，则需要获取该像素的深度z（通过重心坐标插值，作业中已经提示）
  3. 如果“全局变量”depth_buf对于这个点(x,y)存的值要比z还要大，说明需要更新，此时的三角形更接近（需要覆盖原来的），所以保存现在的值，即这个三角形的颜色

那么代码就很容易写出来了：

void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4(); // v表示三角形的三个顶点
    int minx = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
    int maxx = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
    int miny = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
    int maxy = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    // Boundary Box

    for (int x = floor(minx); x <= ceil(maxx); x++) {
        for (int y = floor(miny); y <= ceil(maxy); y++) {
            if (insideTriangle(x, y, t.v)) {
                auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w()); // v[i].w表示顶点i的齐次坐标的w分量
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                int index = get_index(x, y);
                if (depth_buf[index] > z_interpolated) {
                    depth_buf[index] = z_interpolated;
                    Eigen::Vector3f color = t.getColor();
                    set_pixel(Eigen::Vector3f(x, y, 0), color);
                } // 需要进行覆盖，此时的三角形更近
            }
        }
    }
}

结果如下：

image-20241205155309189

我们放大来看走样的细节：

image-20241205155359540

可以看出边缘处有很严重的“锯齿状”，所以需要使用MSAA算法进行优化。

2.2 MSAA算法初始版（带有黑边）

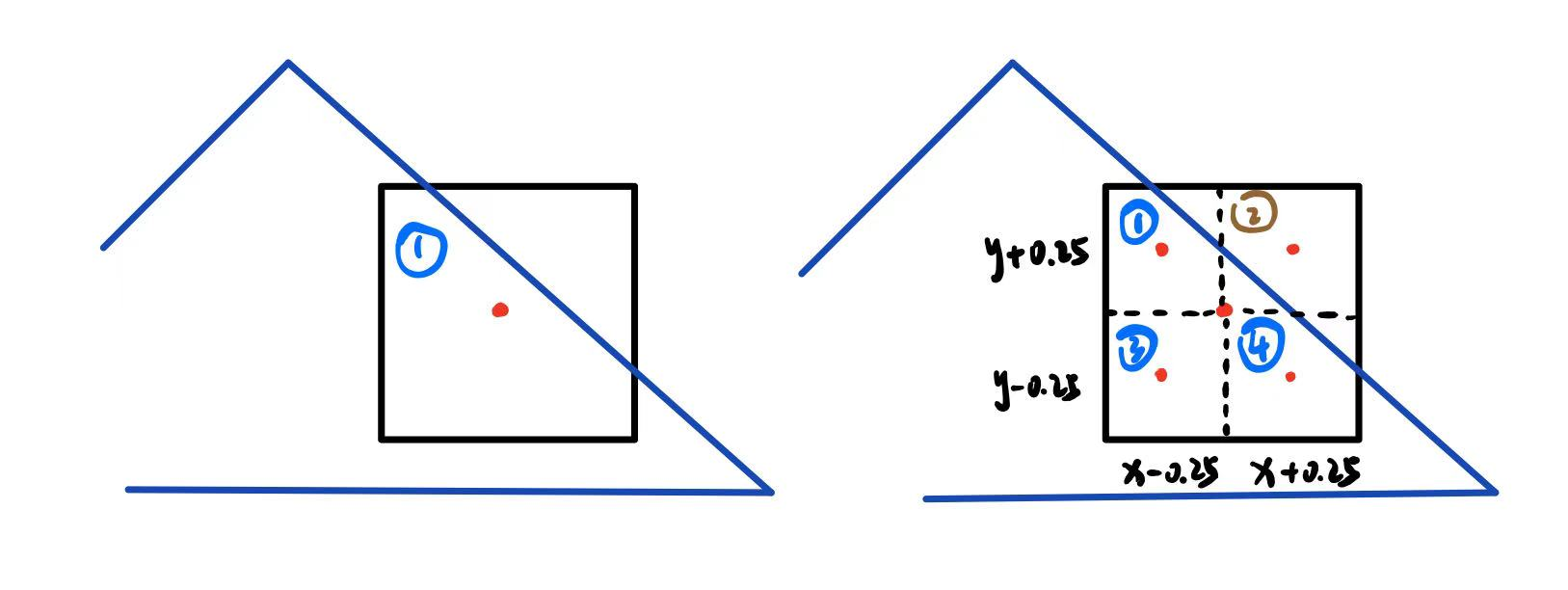
image-20241205160043310

MSAA算法主要是重新进行采样，对于一个像素点不仅仅只看其是否在三角形内（左图），而是对于它附近的四个进行查看并做贡献（右图）。

  • 我们先看左图，在之前的算法中，如果一个像素的中心在三角形内，那么这个像素就是该三角形的颜色，这显然是不对的。如图中在边缘的情况下，明明有很大一部分不在三角形内，却认为这一部分就是蓝色。当然，从贡献的角度上来看，它应该是\frac{\text{在三角形内面积}}{该像素总面积}，那么我们应该如何做呢？
  • 我们再来看右图，这里选择四倍的采样，对于一个点的附近四个点进行选择，判断这四个点是否在该三角形内并计数，按照计数做出贡献。所以图中的这个点应该做出\frac{3}{4}蓝色的贡献，也就是这个像素应该是该三角形颜色的\frac{1}{4}

那么就很好修改了，只需要考虑附近的四个点，写一层循环遍历一下附近的四个点，但是由于我们是0-index，所以我们对于当前像素(x,y)考虑的是(x+0.25,y+0.25)、(x+0.75,y+0.25)、(x+0.25,y+0.75)、(x+0.75,y+0.75)。

如果有cnt个点在三角形内，那么就贡献\frac{cnt}{4}的颜色，这个像素点的颜色就是如此。

void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4(); // v表示三角形的三个顶点
    int minx = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
    int maxx = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
    int miny = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
    int maxy = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    // Boundary Box
    float dx[4] = {0.25, 0.25, 0.75, 0.75}, dy[4] = {0.25, 0.75, 0.25, 0.75};
    for (int x = floor(minx); x <= ceil(maxx); x++) {
        for (int y = floor(miny); y <= ceil(maxy); y++) {
            int cnt = 0;
            float pixelR = 0, pixelG = 0, pixelB = 0;
            for (int i = 0; i < 4; i++) {
                float nx = x + dx[i], ny = y + dy[i];
                // debug2(nx, ny);
                if (insideTriangle(nx, ny, t.v)) {
                    cnt++;
                }
            }
            if (cnt > 0) { // 有点在三角形中
                auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w()); // v[i].w表示顶点i的齐次坐标的w分量
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                int index = get_index(x, y);
                if (depth_buf[index] > z_interpolated) {
                    depth_buf[index] = z_interpolated;
                    Eigen::Vector3f color = t.getColor() / 4.0 * cnt;
                    set_pixel(Eigen::Vector3f(x, y, 0), color);
                }
            }
        }
    }
}

那么这个时候来看效果

image-20241205160923493
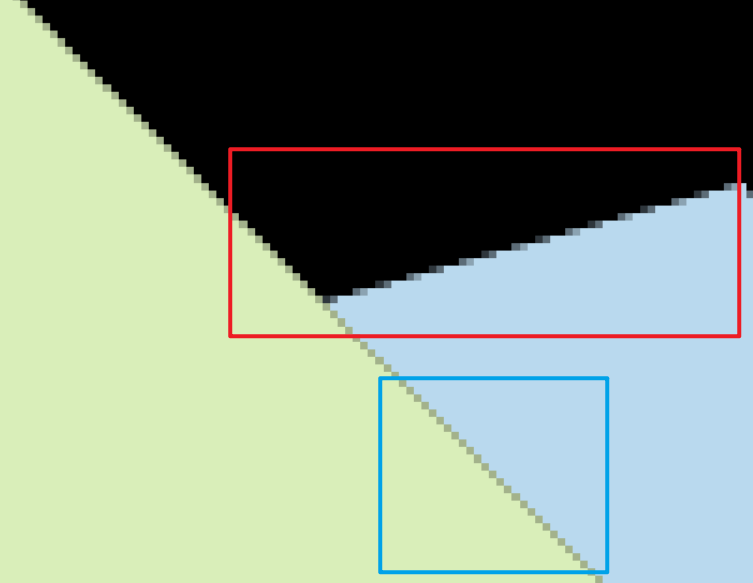
image-20241205161043240

从红色方框上来看可以看出我们在边缘地方已经拥有了“渐变”的功能，这让我们在总体上完成了MSAA算法，在边缘处不会有那么明显的走样。

2.3 黑边问题分析

在蓝色方框处可以看出，在这一部分拥有了黑边，这是因为我在考虑绿色的三角形的时候，对于点(x,y)只会考虑在它的三角形内对于depth_buf[(x,y)]做出的贡献，而如果此时另外不在它这个三角形的点，而在另外一个三角形呢？在这个算法就会进行抛弃。

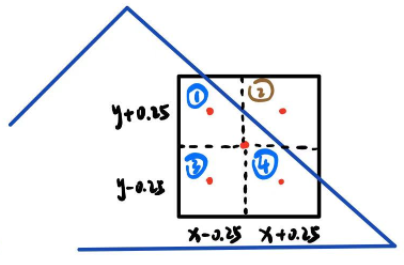
也就是说，我们再来看这个图，1、3、4都在蓝色三角形内，而2在棕色三角形内（假设），那么这个像素点(x,y)的颜色应该由它们两个共同做出贡献，而不是只看(x,y)在哪个三角形内而已。

2.4 MSAA算法（完整版）

那么我们需要一个更多的depth_buf来存储每个像素的四个采样点的深度，最后遍历完所有的三角形之后对于每一个像素统一进行填充颜色（但是在这里写在了每一个三角形后）

我设置了一个结构体：

struct Pixel4x {
    Eigen::Vector3f color[4];
    float depth[4];
};

保存每个像素有四个采样点的颜色以及对应深度，而对于每个点(x,y)的采样点(nx,ny)进行2.1中的算法，填充到pixels中（而不是depth_buf）中。最后对于每一个像素进行颜色的加和，当然，每一个点的颜色贡献是\frac{1}{4}.

void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4(); // v表示三角形的三个顶点
    int minx = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
    int maxx = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
    int miny = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
    int maxy = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    // Boundary Box
    float dx[4] = {0.25, 0.25, 0.75, 0.75}, dy[4] = {0.25, 0.75, 0.25, 0.75};
    for (int x = floor(minx); x <= ceil(maxx); x++) {
        for (int y = floor(miny); y <= ceil(maxy); y++) {
            for (int i = 0; i < 4; i++) {
                float nx = x + dx[i], ny = y + dy[i];
                // debug2(nx, ny);
                if (insideTriangle(nx, ny, t.v)) {
                    auto [alpha, beta, gamma] = computeBarycentric2D(nx, ny, t.v); // 计算插值系数
                    float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w()); // v[i].w表示顶点i的齐次坐标的w分量
                    float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                    z_interpolated *= w_reciprocal; // 当前深度
                    int index = get_index(x, y);
                    if (pixels[index].depth[i] > z_interpolated) {
                        pixels[index].depth[i] = z_interpolated;
                        Eigen::Vector3f color = t.getColor();
                        pixels[index].color[i] = color;
                    }
                }
            }
        }
    }
    for (int x = floor(minx); x <= ceil(maxx); x++) {
        for (int y = floor(miny); y <= ceil(maxy); y++) {
            int index = get_index(x, y);
            Eigen::Vector3f color = Eigen::Vector3f(0, 0, 0);
            for (int i = 0; i < 4; i++) {
                color += pixels[index].color[i];
            }
            color /= 4.0;
            set_pixel(Eigen::Vector3f(x, y, 0), color);
        }
    } // 写在了此处，应该是所有三角形遍历完之后进行，我认为都可以
}

结果如下：

image-20241205162402901

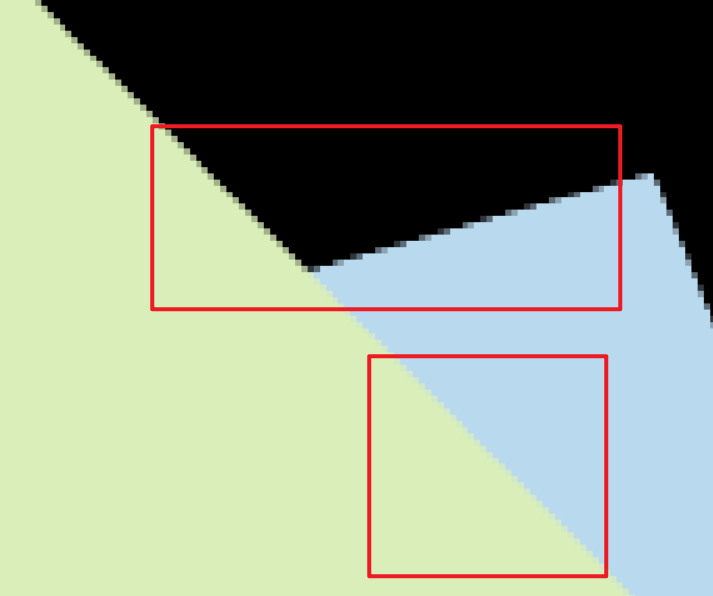
可以看出我们在边缘和黑边问题都进行了改善，减少了走样的问题以及两个三角形覆盖边缘处的黑边。缺点当然就是我多用了空间和时间，可以明显感觉到它变慢了。

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注