Consistent Point Orientation for Manifold Surfaces via Boundary Integration

项目代码：https://github.com/liuweizhou319/BIM

论文：https://dl.acm.org/doi/abs/10.1145/3641519.3657475

相关链接：
🔗PGR论文【法向一致】Surface Reconstruction from Point Clouds without Normals by Parametrizing the Gauss Formula（PGR）
🔗Voronoi图和Delaunay图介绍 - CarryNotKarry

Abstract 摘要

广义卷绕数（generalized winding number, GWN）场具有跳跃边界条件，并且偏微分方程的解具有调和性质。GWN场的狄利克雷能量可以定义边界曲面上的积分。我们构建了一个由GWN的狄利克雷能量导出的边界能量。

以具有随机方向法线的点云作为输入，优化能量来恢复GWN场的全局调和性，从而恢复全局一致法线。

1. Introduction

（说一些有用的）

现有方法及其局限

• 传统基于邻域的法向估计＋传播翻转。缺点是在噪声多、采样稀疏的小reach区域表现欠佳
• iPSR（一种基于 Poisson 重建迭代修正法向的方法）对稠密点云效果好，但在稀疏区域可能产生错误法向，导致重建断裂
• 深度学习方法

广义卷绕数（GWN）的优势

• GWN 能够将三维表面分割为“内外”区域，是区分点云或网格面片方向的有力工具。

• 先行工作中，Takayama 等用最小化 GWN 的 Dirichlet 能量来定向三角面片；Barill 等把 GWN 引入点云估计；PGR、GCNO 等近作则对点云中 GWN 值进行正则化，但计算开销大，对复杂拓扑和薄结构仍缺乏鲁棒性。

这里内外分割区域当然就是内部卷绕数为1,外部为0,这样可以区分是内还是外

本文思路与贡献

• 把 GWN 场的 Dirichlet 能量转换为对点云“边界”表面的积分，提出全新的边界能量。
• 将每个点的法向量作为可优化变量，通过最大化边界能量（并施加 GWN 值范围约束），使 GWN 场满足调和性与跳跃边界条件，从而恢复全局一致的法向方向。
• 采用高效的 L-BFGS 优化器进行迭代，实验证明在噪声、多拓扑结构及薄壳场景下均超越现有最优方法。

2. Related Work

（精读嘛，详细讲述一下）

全局点云法向定向（Global Point Orientation）

• 早期
  • Hoppe（1992）使用PCA进行估算，然后领域传播翻转，奠定了基础
  • 后续基于传播或能量最小化（但对噪声和离群点敏感）
• 隐式函数与距离场
  • 通过拟合符号/无符号距离场或将点云视作偶极子，构建 GWN 场（Mullen 等 2010、NGLO [Li et al. 2023a]、NeuralGF [Li et al. 2023b]、Dipole 方法 [Metzer et al. 2021] 等）
  • iPSR(Hou et al. 2022)，迭代地将前一轮估计的法向输入到 Poisson 重建（PSR）中，在稀疏处不佳
  • PGR进一步将GWN和指示函数参数化。【表面重建】Surface Reconstruction from Point Clouds without Normals by Parametrizing the Gauss Formula（PGR）- CarryNotKarry

PDE 与跳跃边界条件（PDEs with Jump Boundary Conditions）

跳跃边界条件用于描述跨界面的物理或几何属性不连续性。

表面重建：从一致法向推导隐式函数，PSR 求解时满足跳跃条件（Kazhdan & Hoppe 2006；Barill et al. 2018）

3. Preliminaries（预备知识）

\Omega\in\mathbb{R}^3是一个实心物体，表面边界记为\part \Omega。点云\mathcal{P}=\{p_i\mid p_i\in \part \Omega\}_{i=1}^n表示从流形表面上采样得到的n个点。对于每一个点p_i用\hat{n}_i表示其向外的一致法向量，内积用\langle \cdot,\cdot\rangle来表示

3.1 Poisson’s Equation with Jump Boundary Conditions

【Poisson 方程】（带源项的拉普拉斯方程）及其与跳跃（jump）边界条件一起，在物理、科学计算和几何处理中应用广泛。

方程如下：

\Delta u(x) = f(x), \quad x \in \mathbb{R}^3 \setminus \Omega\tag{1},

这表示在物体外部区域上，u满足带源项f的Poisson方程。

Poisson方程就是满足上面的式子，并且f(x)是源项(source term)，它表示在空间中每个点 x 处有多少“生成”或“消耗”量

【Dirichlet 跳跃条件】在物体表面 \partial\Omega 上，强制 u 从内部到外部发生常数 k 的值跳跃：

u^+(x) - u^-(x) = k, \quad x \in \partial \Omega\tag{2},

• u^+(x)表示沿外法向在点x处的极限值。u^+(x)=\lim _{\varepsilon\rightarrow 0} u(x+\varepsilon \mathrm{n_x})

• u^-(x)表示沿内法向在点x处的极限值

这样刻画了跳跃

【Neumann 连续条件】为了保证跨界面的通量连续，还要求法向导数在边界上相等

\frac{\partial u^+}{\partial n_x}(x) = \frac{\partial u^-}{\partial n_x}(x),
\quad x \in \partial \Omega,\tag{3}

\dfrac{\part}{\part n_x}表示统一外法向n_x的方向导数

【Dirichlet 能量最小化】在无源情况下（f=0），解 u 不仅满足上述边界条件，还最小化全域的能量

E[u] = \int_{\mathbb{R}^3 \setminus \Omega} \|\nabla u(x)\|^2 \,\mathrm{d}V.

能量最小化意味着 u 在域外尽可能“平滑”，这一性质为后续将广义绕数场视为谐解并用它的能量形式进行优化提供了理论依据。

3.2 Boundary Integral Equation（边界积分方程）

BEM 先将微分方程等价地写成边界积分方程，然后只对边界 \partial\Omega 进行离散化，得到一个关于边界未知量的线性方程组

使用满足\Delta G(x,y)=\delta_y(x)的Green函数G(x,y)和Poisson核P(x,z)，可以把公式(1)改写如下边界积分公式(4)

u(x)
  = \int_{\mathbb R^3\setminus\partial\Omega} G(x,y)\,f(y)\,\mathrm{d}y
  \\
    + \int_{\partial\Omega}\Bigl[
         P(x,z)\bigl(u^+(z)-u^-(z)\bigr)
         - G(x,z)\bigl(\frac{\partial u^+(z)}{\partial n_z}
                       - \frac{\partial u^-(z)}{\partial n_z}\bigr)
      \Bigr]\mathrm{d}z\\
  = \int_{\Omega} G(x,y)\,f(y)\,\mathrm{d}y
    + \int_{\partial\Omega} P(x,z)\bigl(u^+(z)-u^-(z)\bigr)\,\mathrm{d}z\tag{4}

符号说明：

• G(x,y)：Green函数满足\Delta G=\delta
• \delta_y(x)：Dirac函数。这表示以y为中心的Dirac函数，将单位源“集中”在点 y
• P(x,z)：Poisson核

G(x,y)的典型形式就是G(x,y)=-\frac{1}{4\pi \Vert x-y\Vert}

Poisson核P(x,y)定义是

P(x,z)=\frac{\part }{\part n_z}G(x,z)

即对第二个变量沿边界法向n_z求导，物理意义是描述边界处单位跳跃对x点的影响

3.3 Generalized Winding Number（广义卷绕数）

这里介绍了广义绕数w(x)并说明如何在离散点云里面近似计算

【广义卷绕数定义】

对于闭合曲面（或流形边界）\part \Omega，广义卷绕数w(x)表示任意点x被这个曲面“绕”了多少圈

w(x) = \int_{\partial\Omega} P(x,z)\,\mathrm{d}z.

Poisson内核P(x,y)是Green函数沿着v_y方向的导数，为

P(x,y) = \frac{\partial G(x,y)}{\partial v_y}
       = \frac{1}{4\pi}\;\frac{\langle n_y,\,x - y\rangle}{\|x - y\|^3}.

给定带一致外法向的点云\mathcal{P}，可以将积分替换为加权和，则有

w(q) := \sum_{i=1}^n a_i\,P(q,p_i)
       = \sum_{i=1}^n a_i\,\frac{1}{4\pi}\,\frac{\langle n_i,\,p_i - q\rangle}{\|p_i - q\|^3}.

• 其中，这里的a_i是p_i点的测地线Voronoi面积，表示它对整体表面积分的贡献
• 计算简化：在实际中，直接在表面计算 geodesic Voronoi 面积很耗时，Barill et al. 建议先将点投影到切平面上，再做二维 Voronoi 分析，以近似 a_i。

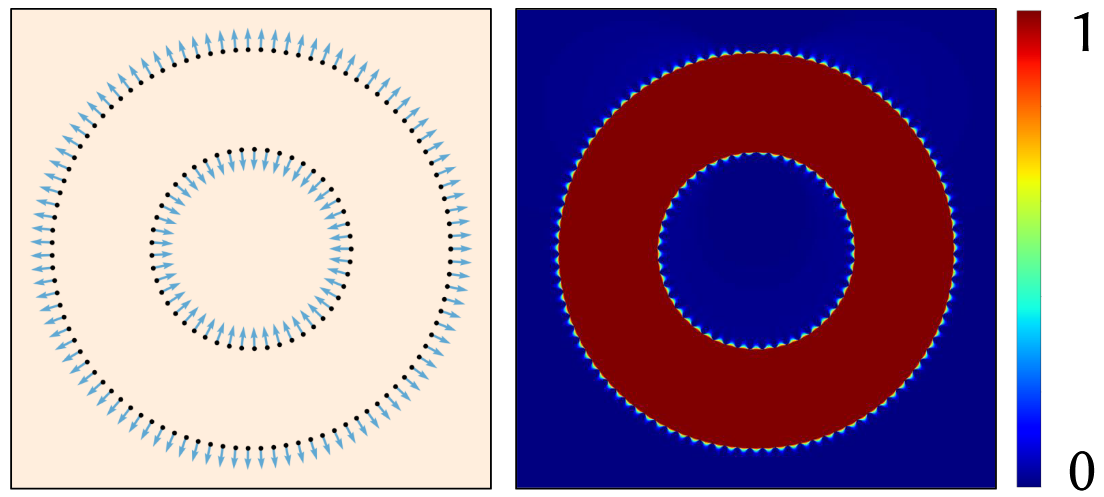
这里的左图表示了法向（蓝色射线），可以从右图看到内部一圈是红色的。

可以从两个地方进行理解：

1. 直观理解，被边界环绕k圈则卷绕数为k，可以看到被环绕了一圈，那么中间值就是1
2. 可以从定义进行推断，加入没有中间那一圈向内的法线，那么外圈里面的w(x)都是1（包括内圈），因为我们从沿法线的u^+(x)到u^-(x)就会变化k，这里(k=-1)。那么再给中间小圈加上去呢？那么内圈就会从原来的1+k=1+(-1)=0

【拉普拉斯方程】当泊松方程源项f(x)\equiv 0的时候，退化成拉普拉斯方程

\Delta u(x)=0

解被称为谐函数

性质

• 在任何小区域内，谐函数的值都等于其边界值的平均（均值性质）。
• 对应无源、无汇的场——例如真空中的电势、无内热源的稳态温度分布。

在无源区间，谐函数也会最小化狄利克雷能量（Dirichlet）

E[u]=\int \Vert \nabla u\Vert^2 \mathrm{d}V

表示它是“最平滑”的可能解

4. Method

输入是一组点云，然后为每个采样点随机指定一个初始单位法向n_i

符号：

• 真实一致法向：\hat{n}=\{\hat{n}_i\}_{i=1}^n，我们希望恢复的目标
• 当前法向场：n=\{n_i\}_{i=1}^n，用于迭代优化
• \Omega^+：外部区域
• \Omega^-：内部区域
• w^+(x),w^-(x)：卷绕场边界的极限，例如w^+(x)=\lim_{\epsilon\rightarrow 0}w(x+\varepsilon n(x))
• 对于边界\Omega^+,\Omega^-有\hat{n}^+=-\hat{n},\hat{n}^-=\hat{n}

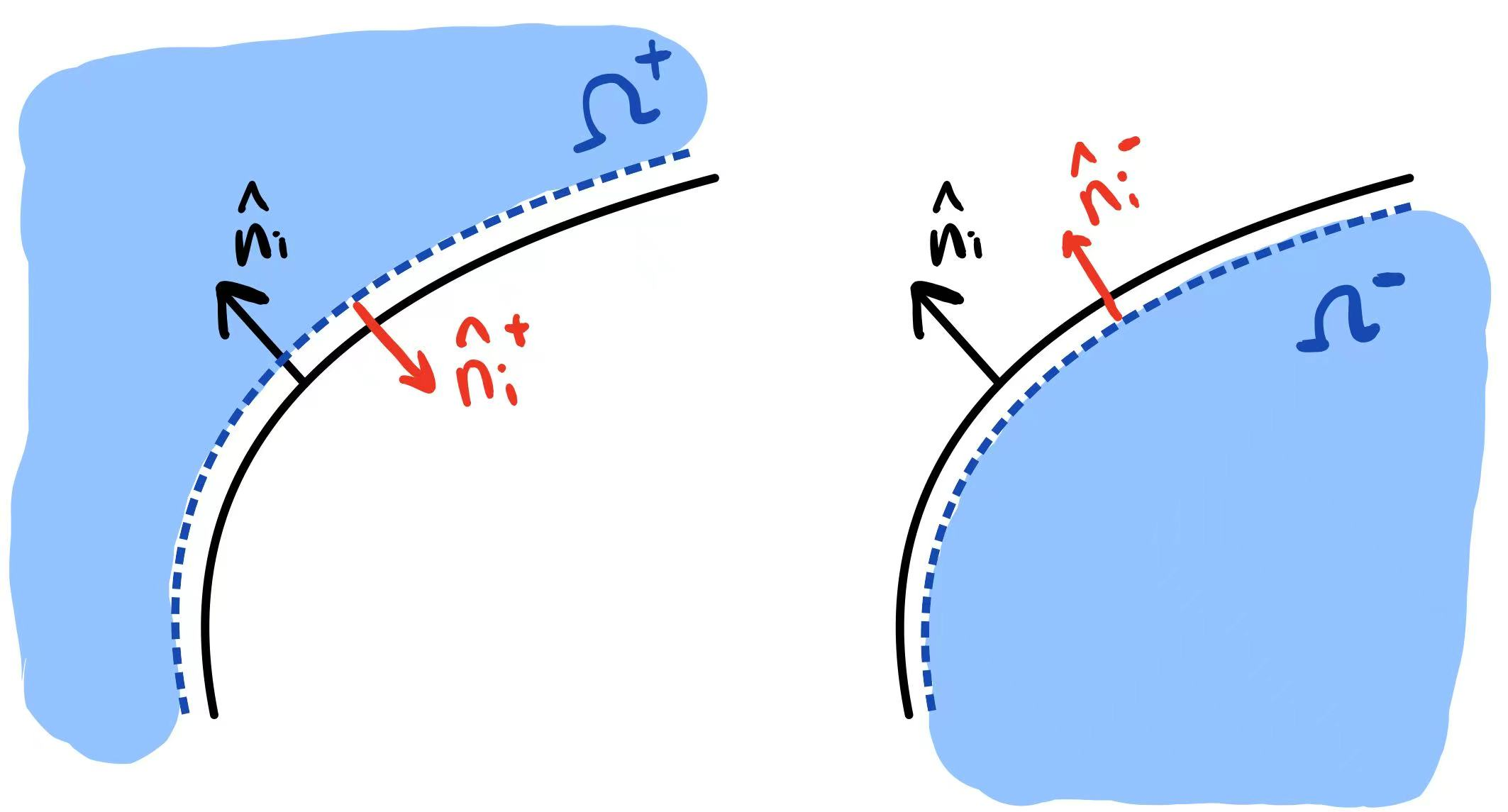
大概表示的就是这个意思

4.1 Boundary Energy（边界能量）

【Dirichlet能量定义】

狄利克雷能量定义在整个空间上，除去表面，定义为：

\min \int_{\mathbb{R}^3\setminus \part\Omega}\Vert\nabla w\Vert^2:=\int_{\Omega^+}\Vert \nabla_w\Vert^2+\int_{\Omega^-}\Vert \nabla_w\Vert^2.

直接在体域上细分并做数值积分需要高质量的四面体网格，计算量大且易出错。

这里\Vert \nabla w\Vert^2等于(\frac{\part w}{\part x})^2+(\frac{\part w}{\part y})^2+(\frac{\part w}{\part z})^2

【Green第一恒等式转为边界积分】

使用Green的第一恒等式格林恒等式-维基百科，可以将上述体积分转化为只在边界上的积分：

\int_{\mathbb{R}^3\setminus\partial\Omega} \|\nabla w\|^2
= 
\int_{\partial\Omega}\bigl(w^- - w^+\bigr)\,\nabla_{\hat n}w^-,\tag{7}

• 这里的\nabla_{\hat n}w^-=\dfrac{\part w^-}{\part n}表示沿全局一致外法向\hat{n}的方向导数，(w^--w^+)则是绕数场的Dirichlet跳跃。

推导：

对光滑区域 U 和标量函数 \phi,\psi，Green 第一恒等式为:

\int_U \bigl(\psi\,\Delta\phi + \nabla\psi\cdot\nabla\phi\bigr)\,dV
= 
\int_{\partial U} \psi\,\frac{\partial\phi}{\partial n}\,dS.

令\phi = w, \quad \psi = w \;\Longrightarrow\;\psi\,\Delta\phi = w\,\Delta w, \quad \nabla\psi\cdot\nabla\phi = \|\nabla w\|^2. 代入得到：

\int_U \bigl(w\,\Delta w + \|\nabla w\|^2\bigr)\,dV
= 
\int_{\partial U} w\,\frac{\partial w}{\partial n}\,dS.

又因为此时满足\nabla w=0（谐函数），则体积分消掉后为：

\int_U \|\nabla w\|^2\,dV
=
\int_{\partial U} w\,\frac{\partial w}{\partial n}\,dS.

接着就是对两侧区域进行合并了，对内部区域和对外部区域有：

\int_{\Omega^-} \|\nabla w\|^2\,dV
= 
\int_{\partial\Omega} w^-\,\frac{\partial w^-}{\partial n}\,dS,\\
 \int_{\Omega^+} \|\nabla w\|^2\,dV
= 
-\int_{\partial\Omega} w^+\,\frac{\partial w^+}{\partial n}\,dS,

合并并利用(\frac{\partial w^+}{\partial n} = \frac{\partial w^-}{\partial n})则：

\int_{\mathbb{R}^3\setminus\partial\Omega} \|\nabla w\|^2\,dV
=
\int_{\partial\Omega}\bigl(w^- - w^+\bigr)\,\frac{\partial w^-}{\partial n}\,dS.

【边界能量】

将法线\hat{n}的狄利克雷能量扩展到任意法线向量场n，定义边界能量f(n)为：

f(n) := \int_{\partial\Omega}\bigl(w^- - w^+\bigr)\,\nabla_{n}w^-\,\mathrm{d}z.\tag{8}

直观感受：

• (w^- - w^+)就是跳跃量，跳跃一个整数
• \nabla_{n}w^-则衡量沿当前法向，绕数场在“内”侧变化的强度

f(n)=\int (\text{跳跃量})\times (\text{沿法线梯度})dz

这个积分越大表示绕数场在界面处跳得足够大（区分内外），场在内侧变化剧烈。

对于任意法向n可以分解为两个部分：

• 切向分量n_t
• 法向分量n_n

n=n_t+n_n

由于导数算子的线性性质，边界能量相应分解为：

f(n)=f(n_t)+f(n_n)

为什么能分解？因为算子\nabla _n=\frac{\part}{\part n}实现性的，所以有\nabla_{n_1+n_2}w=\nabla_{n_1}w+\nabla_{n_2}w，其实就是可以分解成两个向量相加，然后f(x)也是可以线性拆分的，所以有了上式

【\nabla】

这里把标量函数u(x,y,z)变成一个向量场，即

\nabla u=(\dfrac{\part u}{\part x}, \dfrac{\part u}{\part y}, \dfrac{\part u}{\part z})

方向导数\nabla_nu就是把这个梯度向量和一个单位方向向量n做点积，

\nabla_n u=n\cdot\nabla u=n_x\dfrac{\part u}{\part x}+n_y\dfrac{\part u}{\part y}+n_z\dfrac{\part u}{\part z}

表示沿方向 n 上的瞬时变化率。

观察到两点：

【Observation 1】:

法向随机的时候，边界能量的切向分量f(n_t)和法向分量f(n_n)都趋近于0，但Dirichlet能量依然很高。

随机法向导致跳跃很小（正负抵消），但是这并不意味着平滑，因为Dirichlet能量衡量的是整体域外的梯度平方和，随机跳跃无法让场满足真正的谐性

【Observation 2】：

法向全局一致的时候，切向分量f(n_t)\approx 0（卷绕数在切向当然没有变化），而法向分量f(n_n)很大，接近整体边界能量f(n)

绕数场只在法向方向上发生跳跃，切向是平滑的

所有能量都集中在法向方向f(n_n)\approx f(n)，同时场在域外已趋近调和，Dirichlet 能量 也随之大幅降低，与边界能量“对齐”

目标就是最大化边界能量f(n)

\max_{n}\; f(n)\;:=\;\int_{\partial\Omega} \bigl(w^-(z)-w^+(z)\bigr)\,\nabla_{n}w^-(z)\,\mathrm{d}z\tag{9}

• 在所有可能的单位法向场 n 中，寻找能使上述边界积分 最大 的那个配置

我对\nabla算子还是不舒服，我这还是再写一下。

\nabla w(\mathbf{x})是梯度向量，告诉我绕数场w在空间中每个方向上的瞬时变化率：

\nabla w(p) = \left( \frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}, \frac{\partial w}{\partial z} \right) \bigg|_p .

• 如果里表面很远，那么w恒为1或0,那么偏导都接近于0,即\nabla w\approx 0
• 如果正好穿过表面，从0跳到1,梯度并未一个数字1,而是一个分布，梯度非常大，梯度趋近于一个\delta分布，体积分非常大（为什么不是1呢？因为梯度还要除以厚度，厚度无限非常薄，那么此时就很大）

直到现在，我们有两种能量：

• Dirichlet能量：体积分\int \Vert \nabla w\Vert^2
• Boundary能量：边界积分f(n)，没有平方

它和 Dirichlet 体积分相等（Green 恒等式）——但只在真正一致的法向场下二者才严格相等；

在任意法向场下，boundary 能量更专注于“跳跃强度”，而且只需在点云表面上离散积分，计算要轻便得多

在论文的Remark1里面也写到，表面上f(n)和Dirichlet能量\int \Vert \nabla w\Vert ^2都与梯度有关，但是本质是不同的

• 当法向真正垂直于表面的时候，二者才会相等
• 对于任意法向场n，二者通常会相互背离

进一步说明：

Dirichlet 能量 是一个体积分，衡量整个域外的梯度平方和，依赖于场在所有方向上的平滑度。

Boundary energy 只是沿边界的一个特定投影（跳跃方向的梯度），更聚焦于法向一致性。（一致的话最大，没有抵消）

重点来啦

所以，思路就是这样的

1. Green 恒等式（在满足跳跃和 Neumann 条件的解上）告诉我们

   \int_{\mathbb{R}^3\setminus\partial\Omega}\|\nabla w\|^2\,dV
   =
   \int_{\partial\Omega}(w^- - w^+)\,\frac{\partial w^-}{\partial \hat n}\,dS
   = f(\hat n),

其中 \hat n 是“正确”的外法向场。

2. 优化目标
   我们把法向当成变量 n，构造

   f(n)
   = \int_{\partial\Omega}(w^- - w^+)\,\nabla_{n}w^-\,dS

对任意 n，f(n) 都是一个边界上的积分，但只有当 n=\hat n（法向完全正确）时，它才等于体积分 \int\|\nabla w\|^2。

3. 最大化边界能量 ⇔ 最小化体积分

   • 对所有可能的法向场 n 进行搜索，令 f(n) 尽可能大；
   • 当 f(n) 达到最大值时，恰好对应着使得 \int\|\nabla w\|^2 最小的法向配置；
   • 在这个最优点上，二者严格相等。

有两种情况：A（边界有4条外法线），B（边界2外2内）

A：边界能量最大f(n)\approx 4g（g表示沿正确法向的单位方向导数幅值），Dirichlet能量达到最小

B：边界能量f(n)\approx 2g+2(-g)=0，Dirichlet能量很大

• 在理想的情况下（A），w仅存在表面一个无穷薄的层里完成1到的跳跃，梯度可能很大，但还需乘以厚度的积分之后就是一个有限值，即\int_{跳跃层}\Vert \nabla w\Vert ^2\mathrm{d}V

• 当法线混乱的情况下（B），w不能在一层极窄的区域从1到,而是一个较大的范围内缓慢过度，导致\Vert \nabla w\Vert^2在较大体积内都保持中等以上的值，所以体积分E_{Dir}=\int \Vert \nabla w\Vert^2 \mathrm{d}V很大

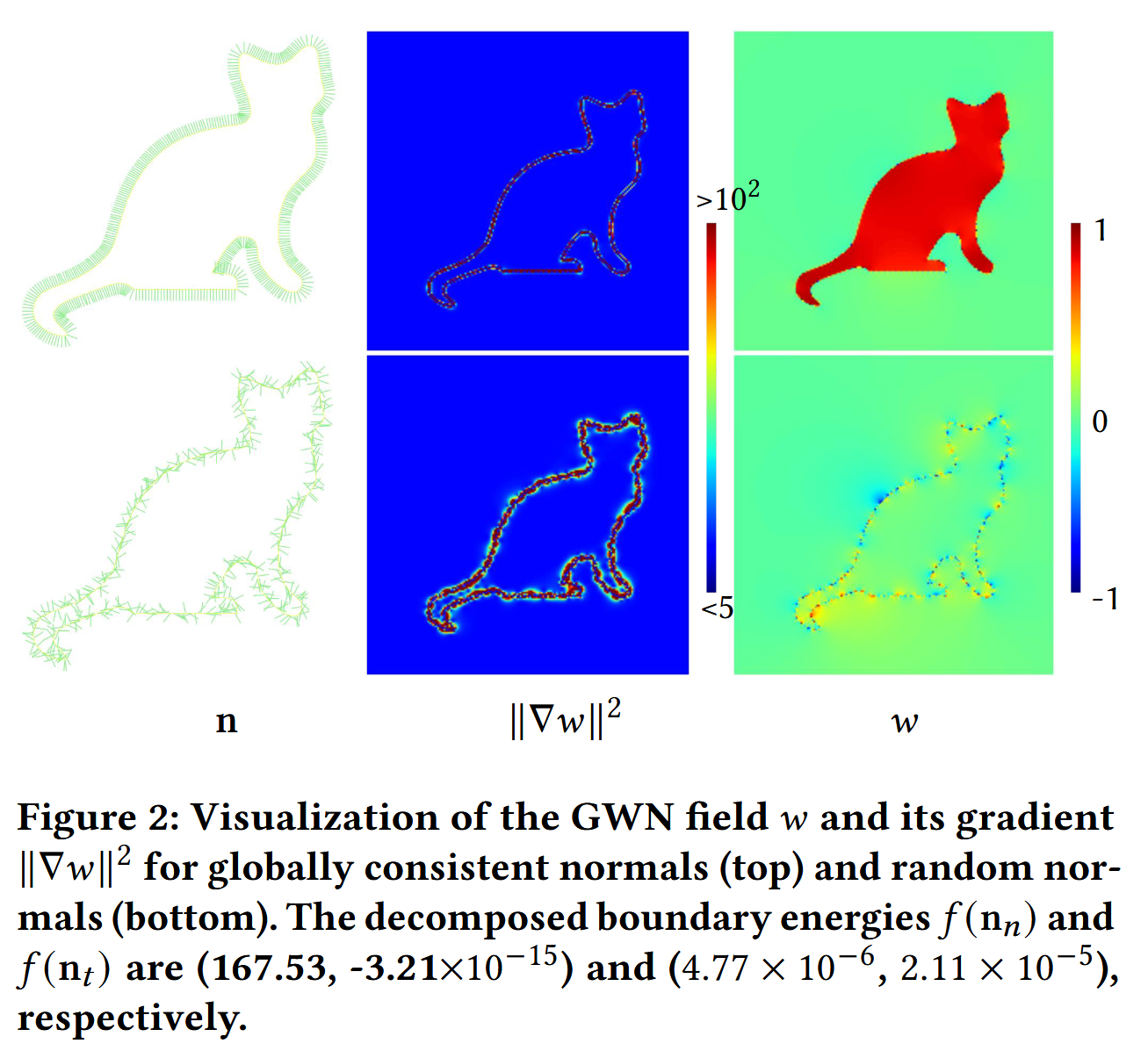
上面的是法向一致的，下面耳朵是混合法向的。中间是Dirichlet能量，可以看到法向一致的时候只有表面才有，而混合的时候整个轮廓乃至外围idou成仙了大量的黄色和红色，大范围梯度产生导致能量高（体积分）。右边展示了绕数场。

4.2 Discretization（离散化）

采样GWN场，对公式(9)转为点云上可计算形式的时候，核心问题在于如何在每个输入点p_i获得“外侧”和“内侧”的卷绕数以及对应的方向导数

f(n)\;\approx\;\sum_{i=1}^n a_i\bigl(w^-(p_i)-w^+(p_i)\bigr)\,\nabla_n w^-(p_i).

• 这里的a_i表示第i个点的Voronoi面积，作为权重
• w^+(p_i),w^-(p_i)分别是内外的近似值
• \nabla_nw^-(p_i)是沿当前法向n_i在内侧的方向导数

一种简单的方法是取增加一个\varepsilon但是在薄结构或者高曲率的时候，通常会落到同一侧，很难区分

【Voronoi 顶点采样】

• 构建输入点云的三维 Voronoi 图，并用一个足够大的包围盒将其各无限单元截断。

• 对于每个 p_i，收集其 Voronoi 单元 \Omega_i^{\rm vor} 上所有顶点（包括截断边界上的顶点）作为候选。

• 从中选出两个顶点：一个最靠近 p_i + \delta\,n_i（外侧候选），一个最靠近p_i - \delta\,n_i（内侧候选），分别记作 p_i^+ 和 p_i^-。

• 实验表明，Voronoi 顶点天然地分布在表面两侧，即便有少量噪声，它们也能可靠地区分内外。

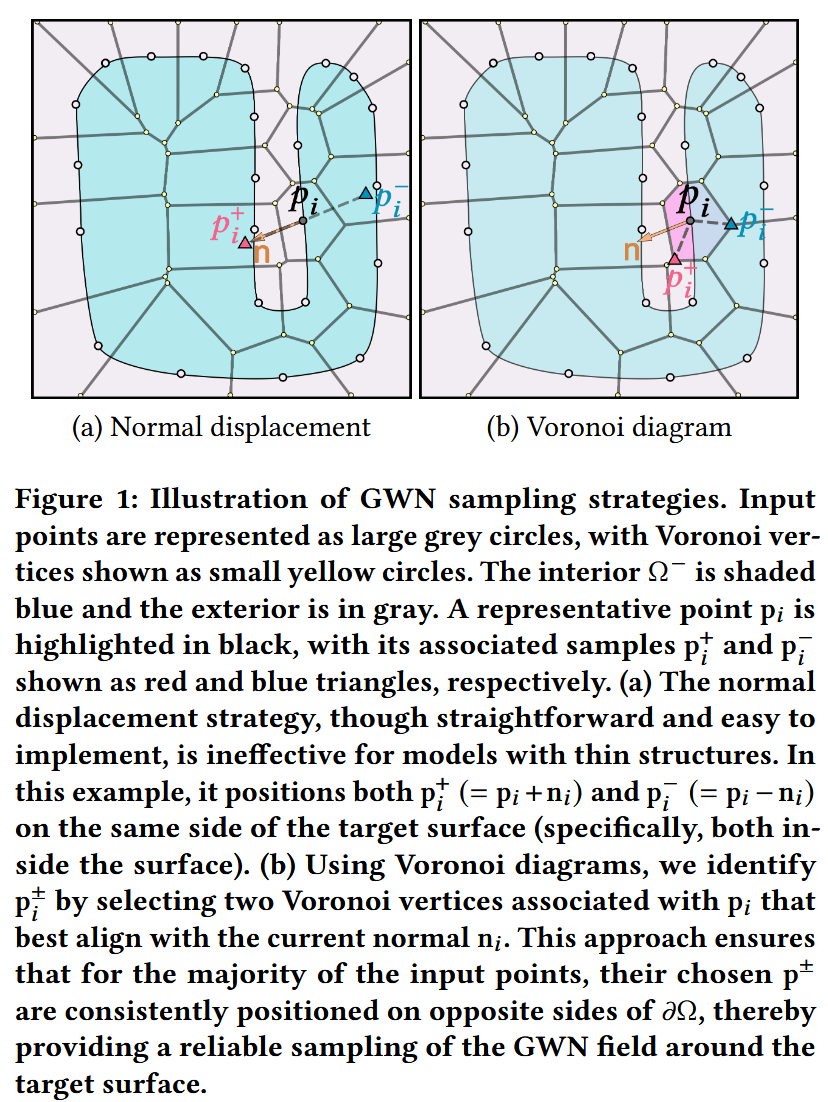
Remark2

对于Inside-out问题，一开始部分p_i^+和p_i^-可能会选错，但最大化能量过程不受阻，随着迭代会修正

这里我有些自己的想法，我也会在一篇文章更新Voronoi图。

1. 为什么要用Voronoi图？为什么能够选到内外两侧？

   那么极端一点，假如是一个在三维空间中的二维平面，那么这个Voronoi图也只会是在平面上对吧？如何选取到p_i的边界外呢？

   不然。在三维空间对于流形上的表面做Voronoi图则会得到一个三维空间的Voronoi图。拿到的那些顶点绝大多数情况都不在原始平面上，正好落在“上方”或“下方”。每一个种子p_i的Voronoi单元都是一个三维的凸多面体。这样天然能获得内外两侧。

2. 如何获得Voronoi图

   从二维来看，对线段做垂直平分线就可以，三维的话就是垂直评分面。

   二维的顶点是三点确定的外接圆的圆心（外心）；三维的是由四点确定的外接球的球心（外心）

【能量最大化】

现在公式(9)的离散形式是：

\max_n\sum_{i1}^n a_i(w^-(p_i)-w^+(p_i))\nabla _{n_i}w(p_i)

• \nabla _{n_i}w(p_i)表示的是绕数场w在p_i处沿当前法向n_i的方向导数

跳跃歧义（Ambiguity in Jump Conditions）

直接最大化上述边界能量，会出现两种“假合法向”都同样能让跳跃看起来正确，但实际却不是我们期望的绕数值分布

1. Case1（负值情况）：

   w^+=-1,w^-=0\quad  \Rightarrow\quad w^--w^+=0-(-1)=1

卷绕数本应内部为1,外部为，跳跃大小仍然是1但这里相反导致错误

2. Case2（超1情况）:

   w^+=1,w^-=2\quad  \Rightarrow\quad w^--w^+=2-1=1

数值超过了[0,1]，但毫无疑问是错误的

如果直接增加约束0\leq w(p_i^\pm)\leq 1,但是会带来2n个不等式，增加了难度

软惩罚代替硬约束

• 惩罚Case1（负值情况），鼓励w\geq 0
• 惩罚Case2（超1情况），鼓励w\leq 1

用绝对值替换，将原来的w^-(p_i)-w^+(p_i)改为

| w(p_i^-)|-|w(p_i^+)|

这样当w(p_i^+)\lt 0或者w(p_i^-)\lt 0的时候会变小，得到沉浮尬

增加软惩罚项g，对内外侧定义：

• 鼓励w(p_i^+)\geq 0（惩罚Case1）：

  g_1(w(p_i^+))=1-e^{\min{\{w(p_i^+),1\}}}

• 鼓励w(p_i^-)\leq 1（惩罚Case2）：

  g_2(w(p_i^-))=1-e^{\max{\{w(p_i^-),1\}}}

• 合并得到

  g(w(p_i^\pm))=1-e^{\min{\{w(p_i^+),1\}}}+1-e^{\max{\{w(p_i^-),1\}}}

最终的问题转化为了：

\max_{n}\;
\sum_{i=1}^n
a_i\Bigl(\,\bigl|w(p_i^-)\bigr| - \bigl|w(p_i^+)\bigr|\Bigr)\,
\nabla_{n_i}w(p_i)
\;+\;
g\bigl(w(p_i^\pm)\bigr).

这是一个无约束的、对 n 平滑可微的优化目标

参数化与迭代

使用L-BFGS求解上述问题。

为了保持每个法向n_i为单位向量，才用球坐标参数化

n_i=\begin{pmatrix}
  \cos u_i\ \sin v_i \\
  \sin u_i\ \sin v_i \\
  \cos v_i
\end{pmatrix}

这样将u_i,v_i作为优化变量

Remark3:既是偶尔选出的p_i^+和p_i^-在同一侧，惩罚项g也能使这种情况变低，不会在后续迭代中保存下来

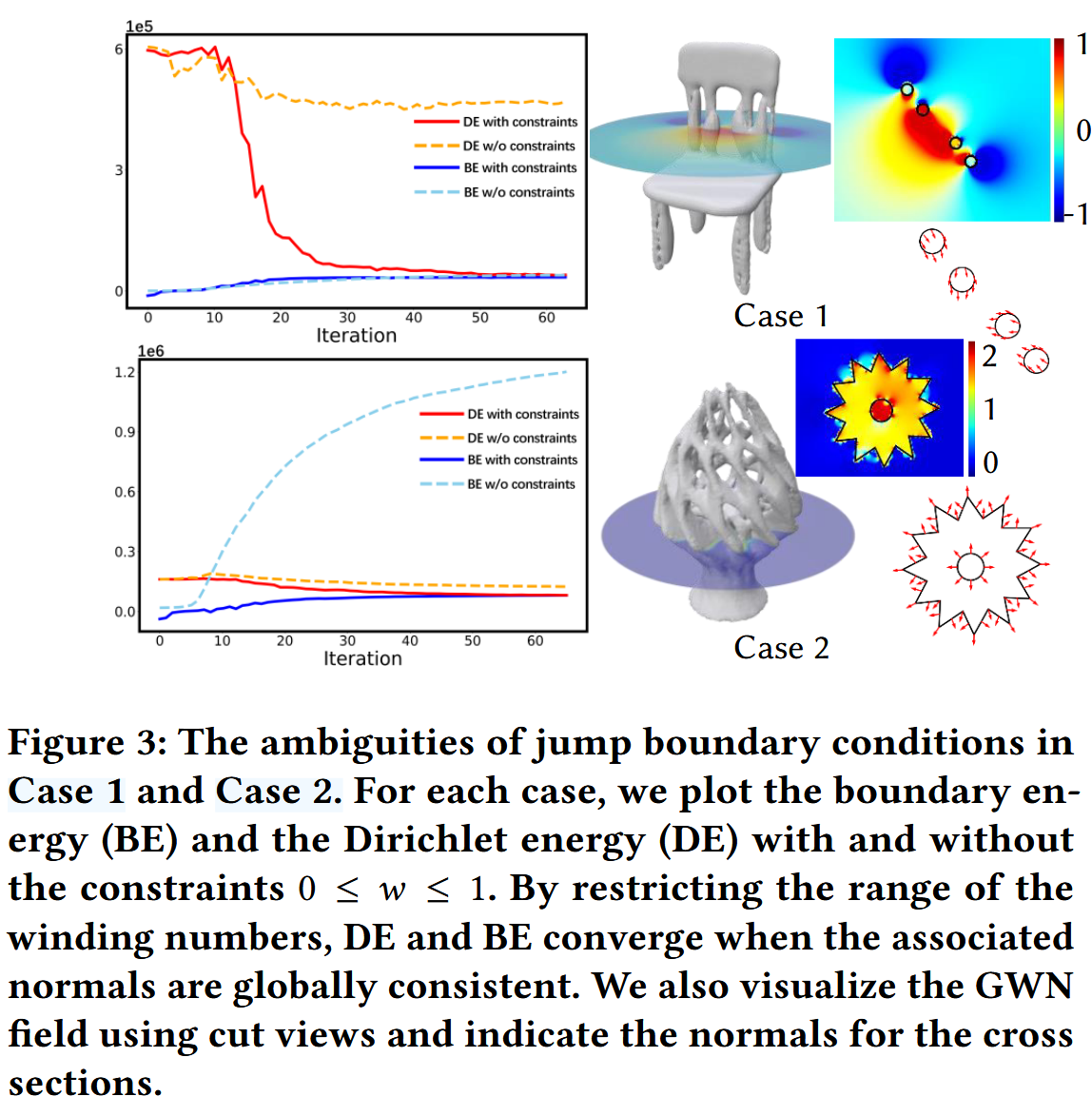
四条曲线分别是：

• DE with constraints（红）：带 0\le w\le1 约束下的 Dirichlet 能量；
• DE w/o constraints（橙虚线）：无约束的 Dirichlet 能量；
• BE with constraints（蓝）：带约束的 Boundary 能量；
• BE w/o constraints（青虚线）：无约束的 Boundary 能量。

右侧示意

• Case 1（上）可视化一个开口椅模型的绕数切面，红蓝渐变显示绕数值分布；旁边小球示意一组朝内法向（虚线）和被误导的样本方向。
• Case 2（下）用一个复杂枝状模型说明在不加惩罚时绕数可跳到 >1（热力图的高值黄色），法向箭头示意歧义部位；加罚后恢复到合理的 [0,1] 跳跃。

Remark4讲到了时间复杂度，可以降到O(n\log n)

4.3 Contrasting Our Method with Previous Approaches

【与Takayama et al. [2014] 的方法对比】

共同点：都最大化最小化能量来进行矫正

	Ours	Takayama et al. [2014]
区别	随机初始化开始	Takayama工作假设输入点云的法向已经垂直表面，只需要翻转即可
	L-BFGS优化器，可以处理百万级以上点云	暴力求解

【与 GCNO [Xu et al. 2023] 的方法对比】

区别如下

	Ours	GCNO
方法论差异	关注边界能量，只需要计算两个采样点p_i^\pm处绕数差值及梯度，避免对GWN精确值的依赖	在所有Voronoi顶点上将GWN正则化到0或1的精确值，依赖于精确的绕数场重构
离散化差异	只在每个 Voronoi 单元中挑选与当前法向最对齐的两个顶点，不依赖“全局均匀分布”假设，更稳健	认为每个点对应的 Voronoi 顶点在内外均匀分布，这对复杂几何（薄结构、高曲率）往往不成立
时间复杂度差异	仅对输入点的两个候选点计算w及一次梯度。复杂度O(n^2+n+m)。主要计算在于构建Voronoi。远小于GCNO	要求所有Voronoi顶点计算卷绕数w，复杂度O(nm)

【与 PGR [Lin et al. 2022] 的方法对比】

	Ours	PGR
正则化对象不同	不对GWN做硬约束，而是对内外绕数差值和梯度做正则化	直接在输入点上正则化GWN值，统一到0.5,但有噪声的情况下难以稳定
求解方法	L-BFGS无约束优化，处理大规模数据且节省内存	求解稠密线性系统，所以限制了只能较小规模