这篇就略读一下,并没有逐步来看了,但是也写了许多笔记,这里稍微介绍一下。
这一篇是做点云生成的,也就是经过大量的训练之后,我输入一些信息就会生成对应的物体,比如”一个蓝色的椅子“就会生成出结果。
这主要的流程就是在潜空间中学习潜向量,然后基于潜向量推导出来一些信息,比如高斯椭球的参数(稍后会讲),主要的过程如下:
-
首先是VAE。VAE作为一个生成模型,就是样本通过编码器网络变换成一个理想的数据分布,然后数据分布再穿递给解码器得到样本。解决问题就是构造编码器和解码器。
-
我们得到了潜向量
Z_0之后,将一个庞大的图形数据转化为一个数据量小的多维向量,比如512\times 16 -
那么我们要学习到
M(M=2048)个面片,经过层层学习得到第l层的潜向量Z_l,形状比如是2048\times 512,这样表达的信息更多了 -
通过
Z_l我们可以通过两个解码器得到信息:面片中心解码器。我们可以从
Z_l特征放到空间中的什么位置,在这里当然是贴在表面面片特征解码器。我们可以获得四个角的特征
f和h(稍后有解释) -
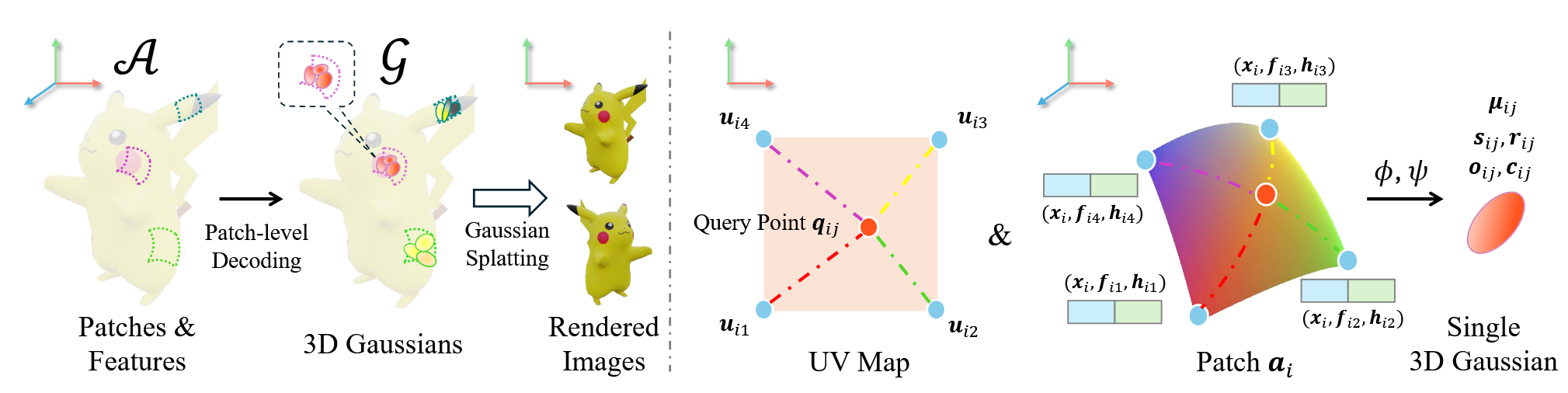
对面片进行
UV空间的采样查询,生成高斯球。
对于查询而言,我们在查询什么?用什么查询?
首先我们要描述这个点云,有很多的方法,比如有mesh、样条等,现在我们用3DGS那样的高斯椭球来描述,我现在有贴在表面的2048个面片,我想要生成100000个高斯椭球来辅助我生成,那么我要对每个面片采样\frac{100000}{2048}\approx 50个,所以我会对每个面片的[0,1]^2空间内随机采样50次得到。
那么对于在[0,1]^2空间内的一点(u,v)怎么获得这个点的信息呢?这里用到的是插值,比如[0.2,0.5],那么我们可以对于角落四个点,通过\sum w_i=1的权重进行插值得到它的特征值f和h,分别是几何信息(位置)以及属性信息(颜色、透明度等)。
分别通过一个简单的MLP可以得到对应的参数,记得位置信息还得加上面片的位置中心才可以得到真实的全局坐标系下的位置。
\begin{aligned}
\mu_{ij}&=\phi(q_{ij},u_i,f_i)\\
\mu_{ij}&=\mathbf{MLP}(\sum_{k=1}^{4}w(q_{ij},u_{ik},f_{ik})\cdot f_{ik})+x_i
\end{aligned}这里的w其实也就是一个归一化的权重
\begin{aligned}
w\left(\boldsymbol{q}_{i j}, \boldsymbol{u}_{i k}, \boldsymbol{f}_{i k}\right) & =\frac{\widetilde{w}\left(\boldsymbol{q}_{i j}, \boldsymbol{u}_{i k}, \boldsymbol{f}_{i k}\right)}{\sum_{l=1}^{4} \widetilde{w}\left(\boldsymbol{q}_{i j}, \boldsymbol{u}_{i l}, \boldsymbol{f}_{i l}\right)}, \\
\text { and } \widetilde{w}\left(\boldsymbol{q}_{i j}, \boldsymbol{u}_{i l}, \boldsymbol{f}_{i l}\right) & =e^{\omega_{2}\left(\boldsymbol{q}_{i j}\right)^{T}\left(\boldsymbol{f}_{i l}+\omega_{2}\left(\boldsymbol{u}_{i l}\right)\right) / \sqrt{d}},
\end{aligned}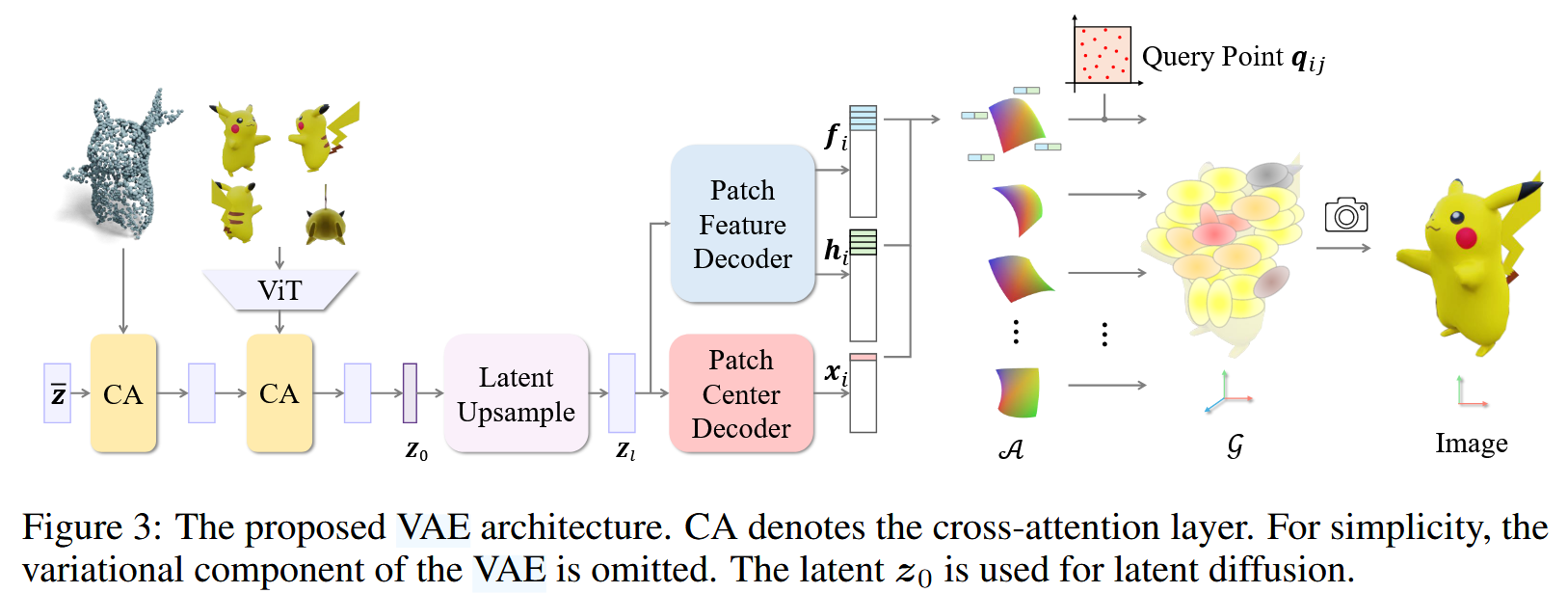
更多的深度学习方面我也不是很懂,我觉得深度学习很黑盒,就是喂数据,这能叫算法吗?也许算,但在我心中的算法是无监督的,这样或许鲁棒性更强,有些深度学习模型只对某一个数据集好,其他的当然就不会展示了。
