LGSur-Net: A Local Gaussian Surface Representation Network for Upsampling Highly Sparse Point Cloud

Abstract

提出了LGSur-Net，端到端，对稀疏点云上采样

核心思路

1. Local Gaussian Representation
   • 在一个局部平面上放置一系列 高斯函数 (Gaussian functions)，作为局部几何的表示。
   • 这些高斯是 可训练的，并且每个高斯的 协方差矩阵 也是优化参数。
   • 相当于：用高斯分布去近似点云局部的连续表面。
2. Feature extraction & attention
   • 从点云及其邻域提取特征（包括边信息），再用 注意力网络 (attention-based network) 学习这些局部高斯表示。
   • 目的是准确刻画局部几何。
3. Gaussian representation 的优势
   • 高斯是连续函数，天然具有 高阶连续性，因此可以更好地拟合平滑曲面。
   • 这让 LGSur-Net 能够预测 表面法向量 (surface normals)，并且支持上采样到任意分辨率。

给我的理解就是，一个点云可以用B样条去拟合，这回是用高斯去拟合，这样所有高斯拼在一起就是一个表面了，这就是通过学习的方法进行的。

Introduction

传统的点云学习方法依赖于点的坐标和特征，但是在稀疏的情况下保持不好，因为学习不到就会乱补，但本篇使用的高斯基函数来显式表示局部表面，而不是神经网络的黑箱学习。

提出了一种局部高斯面的表示

• 首先将稀疏点云投影到某个参数化表面

• 在这个表面防止一系列的高斯基：

G_k(\mathbf{x})=\exp\big(-\frac{1}{2}(\mathbf{x}-\mu_k)^T\Sigma_k^{-1}(\mathbf{x}-\mu_k)\big)

• 最终高斯加权和表示：

S(\mathbf{x})=\sum_kw_kG_k(\mathbf{x})

这里的w_k是可学习的

Attention-based Learning

• 单纯 Gaussian basis 还不够，他们设计了一个 Attention 模块，来根据点云局部邻域的特征，学习如何选择合适的高斯权重和参数。
• 也就是说，网络在学习的不是点的位置，而是如何调整高斯面来拟合局部几何。

Related Work

讲了几类上采样：

1. 基于优化的（Optimization Based）如LOP，WLOP等

2. 基于学习的（Learning Based）如PU-Net、PU-GCN、GAN系列等

   几何中心方法；

   • PUGeoNet： 2D parameter domain采样 提升到3D
   • MAFU： 学习几何约束与插值权重
   • NP：学习几何形状
   • GeoUDF：用二次多项式拟合局部几何 normals

而LGSur-Net定位是：与前人不同：不是直接学习点的分布，也不是拟合多项式，而是 基于高斯基函数 (Gaussian basis functions) 来近似局部 surface patch。这种表征方式，本质上就是“概率分布拟合 + 深度学习”。

Method

局部高斯

主要的步骤大概就是将稀疏点云输入到网络中进行计算，然后对每个点p附近都推断出一种局部高斯的表示，用来近似原始的几何结构。

主要的优点来源于3DGS重建方面的表现出色，以及可塑性强（形状可以进行优化）并且可以微分，可以容易得到法线。

基础思想就是在三维空间中，一个局部曲面可以表示为高度函数z=z(x,y)，类似于一维的拟合，在D_{xy}内分布一系列基点X_t，定义高斯基元：

\phi_t(x)=e^{-\frac{1}{2}(x-x_t)\Sigma^{-1}(x-x_t)^T}-\delta

其中x_t是基点中心，这当然是一个三维坐标，\Sigma是协方差矩阵，最后的\delta就是一个偏差，因为这个是个高度函数。

我理解的是这篇文章并不是场的概念，它就是一种拟合的思想，所以分patch之后需要去拟合，比如在z=3的上方有一个半圆，它并不是从(0,0,0)开始在某个位置有一个高斯，而是直接在z=3的那个平面上有一个高度函数z=z(x,y)，比如圆心在(0,0,3),半径为1,那么此时传入(x,y)=(0,0)就会得到z=1, 众多的高斯合起来就是这个表面。

当然这看起来很蠢，因为我都做图形了，不论我如何刚性变换这个图形它都是这个图形，但是高度函数不是呀，它就是z=z(x,y)。这里作者介绍了一个可以投影到任意平面，而不仅仅是xOy平面（上述例子），引入了一个参数化的局部坐标系来实现的，方程如下：

\begin{cases}
x=a_{11}u+a_{12}v\\
y=a_{21}u+a_{22}v\\
z=a_{31}u+a_{32}v
\end{cases}

这其实就是用参数(u,v)定义了三维空间的一个平面，系数a_{ij}决定了平面的具体方位和三维空间中的朝向，这稀疏是可学习的，最后在局部高斯表示公式:

f_q(u,v)q+A_q\Phi(u,v)

中起到决定性作用的是系数矩阵A_q，为每个点q预测出最优的矩阵A_q

这里的q是来自稀疏点云中的一个具体的点，可以理解为一个局部区域的“锚点”或者“原点”

所以再学习的过程中，对于稀疏点云（输入点云）的每一个点网络都会单独给它预测一个专属的、最适合周围几何形状的矩阵，我们称之为A_{p1},A_{p2},...

投影到任意平面，我们把上面的公式f_q(u,v)q+A_q\Phi(u,v)拆开来看，基函数是：

\Phi(u,v)=[u,v,\phi_1,\phi_2]^T

而矩阵A_q是一个3\times (2+T)的矩阵，列向量就是A_q=[a_1,a_2,...]，二者相乘的时候得到：

A_q\Phi=a_1\cdot u+a_2\cdot v+a_3\cdot \phi_1+a_4\cdot \phi_2+\cdots

注意前两项a_1\cdot u+a_2\cdot v就是这个局部参数平面的基向量，它们定义了一个由参数(u,v)张成的平面，以q为原点，在三维空间中有任意的朝向，最后高斯函数\phi就是在这个基准平面上增加高度，形成曲面。

比如a_1=[1,0,0],a_2=[0,1,0],前者是x轴方向，后者是y轴方向，二者张成出来了一个z=0的平面，那a_1=[1,0,0],a_2=[0,0,1]呢？很显然就是x轴和z轴的形成的那个平面

至此，投影部分讲完了，我还是觉得高度函数很丑...

对于比较震惊的一点，我们来思考它这个有多少个参数。我一开始还觉得丑陋的是对于每一个点是单独来看的，那么对于每一个点都有独立的高斯函数？其实不然，整个过程被分成了4\times 4的网格，对于每一个网格中心都有一个高斯函数，所以一共才16个！

换句话说，我们拿\sin和\cos来举例，在这个图形中有这些基函数，你首先可以通过参数来投影到一个地方，然后再拟合这个部分，那思考一下：“那至于是\sin{2\theta}还是\sin (3\theta+5)那就是学习的权重了，比如矩阵A里面就有2,0或者3,5这样的参数了”。其实是对的，我首先会把学习到的[3,5]加入到sin(x)中，然后再去乘以A矩阵。

那么参数实际上就是3\times 18个，看作列向量分别是a_{1},a_{2},\cdots,a_{18},前面两个定义局部平面的朝向和大小，后面16个作为高斯的权重来和\phi相乘：

A_{q} \Phi(u, v)=\underbrace{a_{1} u+a_{2} v}_{\text {定义基础平面 }}+\underbrace{a_{3} \phi_{1}(u, v)+\ldots+a_{18} \phi_{16}(u, v)}_{\text {在平面上増加高斯形状 }}

私以为可改进的地方:

• 动态的高斯基函数个数
• 高斯基函数位置可学习

网络架构

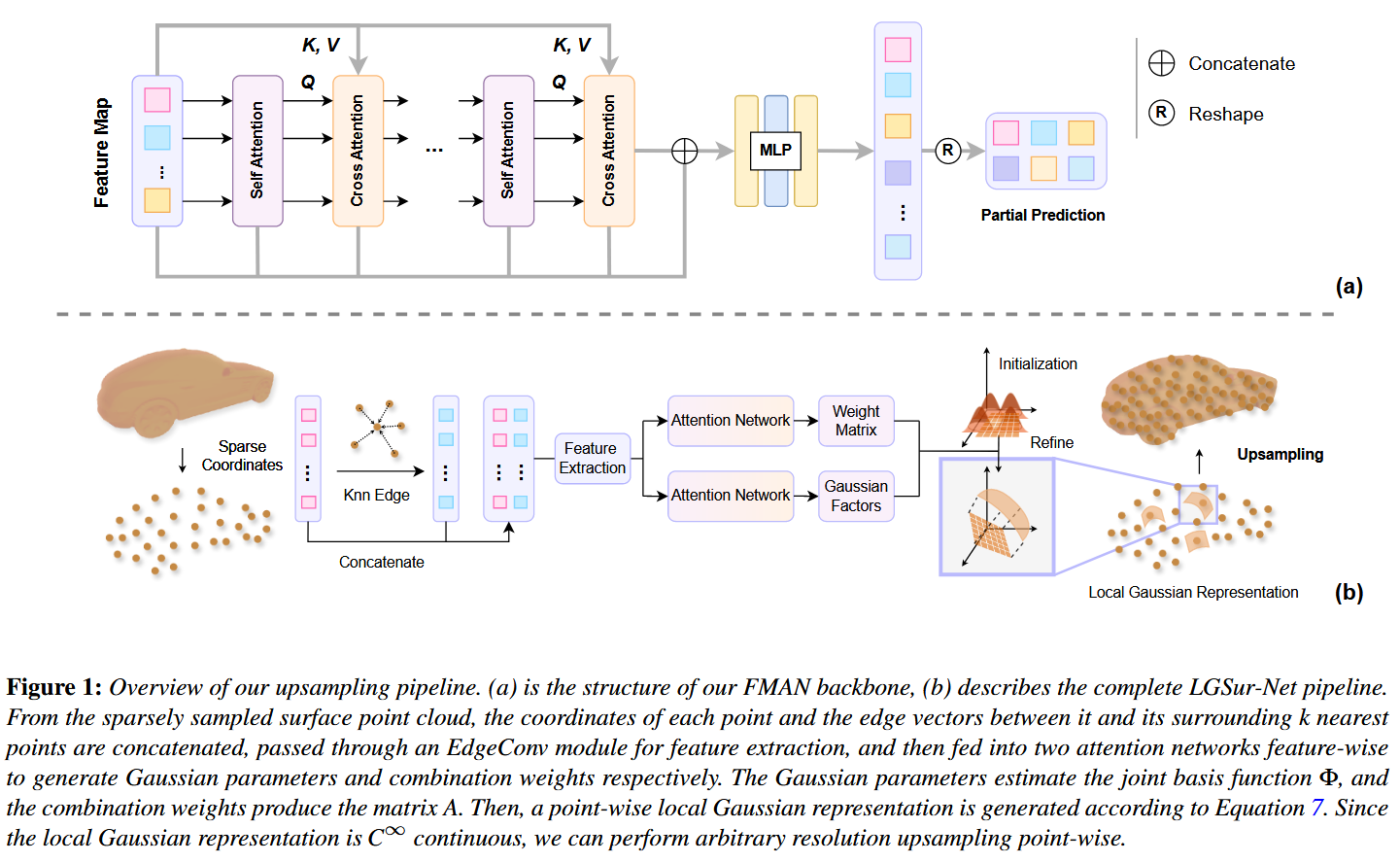
从这图的1(b)来看，首先对于点云的每一个点提取坐标以及周围k个最近邻居点连接成的边向量，拼接起来送入一个EdgeConv的几何特征提取器。生成特征图，这个可以理解为一个信息库，里面存储了点及其邻域的知识。

图送入两个并行的注意力网络中，这两个网络就是FMAN的核心：

• 一个负责生成权重矩阵，也就是之前说的矩阵A
• 一个负责生成高斯因子，也就是高斯基函数的具体形态

而FMAN就是图1(a)所示的了，精妙之处在于反复地、有重点地回顾和查询已经提取出的几何信息。

核心组件在于：

• 自注意力（Self Attention）：元素之间互相关注
• 交叉注意力（Cross Attention）：正在处理的信息流(Query)去关注和查询一个外部的信息源(Key,Value)

重复多次。

这个交叉注意力：

• Query（Q）：来自刚刚经过自注意力处理的主干信息流
• Key（K）和Value（V）：来自于最开始由EdgeConv生成的那个特征图（Feature Map）

这个KV应该不变，Q是一直迭代的。1. EdgeConv产生差异化特征 -> 2. 注意力机制利用并放大这个差异。

比如当前点是x，在边缘edge上，邻近的edge还有点y，flat平面有z，在edgeconv之后它们的差异可能不是很大，但是在注意力机制时候就会利用这个差异：

现在，特征图这个“知识库”里已经存储了能够区分边缘和平面的不同特征了。

1. 当网络的主干信息流处理到边缘点x时，它的状态（Query）会携带“我是边缘”的信号。
2. 这个“边缘”Query去和邻居们的Key做匹配：
   • 它和y的“边缘”Key会高度匹配，得到一个很高的注意力分数。
   • 它和z的“平坦”Key则不那么匹配，只会得到一个较低的注意力分数。
3. 最后，网络根据分数高低，去重点提取和加权邻居们的Value。它会重点“听取”来自y的详细信息，而相对“忽略”来自z的信息。

损失函数

损失函数目标有两个：

1. 生成的点云在空间位置上要准
2. 确保点云构成的局部表面要平滑且法线方向要对

\mathcal{L}_{pu}=\lambda \mathcal{L}_{cd}+\mathcal{L}_n

生成的法线和gt的法线计算公式如下：

\mathcal{L}_{n}\left(N_{g t}, N_{g e n}\right)=\sum_{\mathbf{n}_{i} \in N_{g t}} \inf \left\{\left\|\mathbf{n}_{i}-\mathbf{n}_{j}\right\|_{2} \mid \mathbf{n}_{j} \in N_{g e n} \cup \widetilde{N}_{g e n}\right\}

对于真实法线集N_{gt}中的每一条法线n_i，都会去预测法线集N_{gen}中寻找一个最接近的法线n_j

这里有一个关键的细节是：\widetilde{N}_{g e n}其实是{N}_{g e n}的反方向集合，即-n_j

\inf\{...\}是寻找最小距离，这样可以解决翻转问题

这样也可以吗...

这样的制定标准我用1D举例，假如是2,3,4（按顺序），但结果他们三个都错了，真实的值是4,2,3,那么损失函数是0但他们都不一样啊！

但实际上在代码里面首先计算cd距离，然后再计算法线损失，计算法线损失的时候利用了上一部计算倒角距离得到的最近邻索引，这意味着并不是比较两个毫无关联的法线，而是将一个真实点云中的点P的法线和空间位置上最接近的那个生成点P_{gen}进行比较。

那么如果是2,3,4和4,2,3，2就会找到4

局限性

虽然我们的方法可以有效地致密稀疏的点云，但大量缺失区域的存在可能会导致我们方法的失败。首先，无法检测丢失的零件阻止局部高斯贴片的计算。其次，我们的框架无法在没有中心点的情况下生成补丁，因此很难填充缺失的零件并可能导致故障。