概括
论文链接🔗：https://ojs.aaai.org/index.php/AAAI/article/view/28102
代码链接🔗：https://github.com/lisj575/APU-LDI
由标题可以看出本文主打的是局部距离指标（LDI）；任意倍率；UDF隐式场
思路是由点云pointcloud分成若干个patches，通过训练LDI获得表面信号，再进行拼接。此时的问题存在两个，一个是边界没有全局信息难以确定，还一个就是不一致性，点云可能会出现孔洞。那么此时用预训练好的局部距离指标（LDI）指导全局UDF场的形成。这里还使用到了注意力（Attention-based）模块。
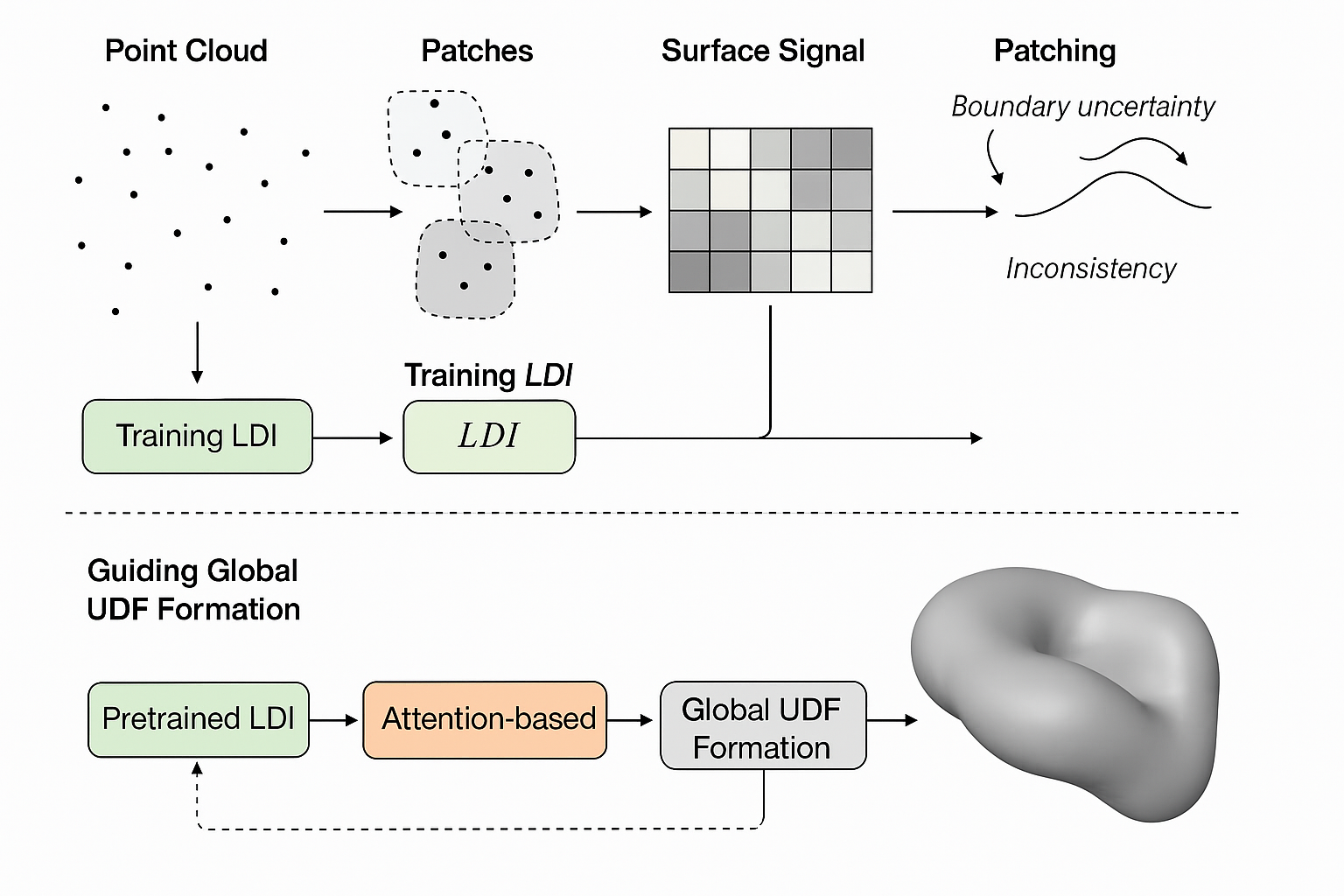
流程是两个：
1️⃣局部学习。patch上训练带有注意力的LDI，掌握“稀疏→密集”的能力。
2️⃣全局学习。讲训练好的LDI去指导全局UDF函数表示连续曲面。
生成方式：物体周围随机撒点，利用UDF计算距离和梯度，梯度反方向拉回表面上。
相关工作（三种）：
1️⃣优化：依赖物体表面是平滑的这一假设
2️⃣学习：问题在于patches的边界
3️⃣隐式：如NeRF，过于平滑、依赖法线
方法
问题概述，输入稀疏点云是包含N点的S，输出稠密点云包含M点的T，尺度因子r=\frac{M}{N}。两个核心的要求：
- 表面保真性（Fidelity）：生成的每一个稠密点应该精确地位于稀疏点云所表示的潜在真实表面上。
- 分布均匀性（Uniformity）：均匀地分布
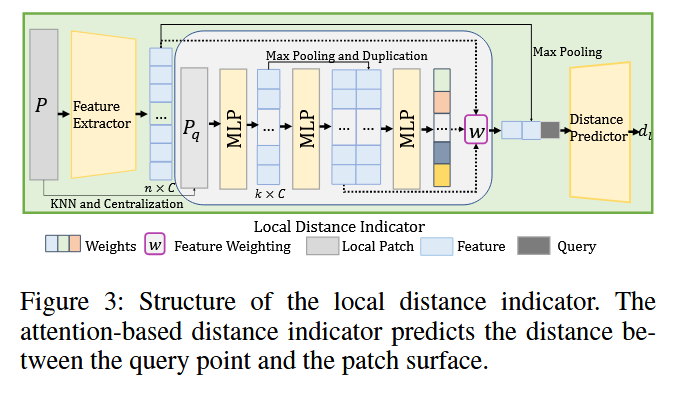
局部距离指标（LDI）
LDI的目标和作用：
- 目标： 为了学习精确的几何细节，作者首先训练一个作为“局部距离指标”的神经网络。
- 作用： LDI是一个“局部专家”。它的任务是，给定一个查询点
q和它附近的一个局部点云块P，它能精准地预测出点q到这个块所代表的局部真实表面的距离d_l。
数学表示： f_θ(q,P)=d_l，其中 f_θ 是LDI网络。
那么如何精准鲁棒来预测距离呢？——注意力模块
步骤1️⃣：邻域构建相对特征
- 对于一个查询点
q，首先用KNN算法在它所属的局部块P中找到k个最近的邻居点，形成一个更小的邻域P_q。 - 将这个邻域
P_q的坐标进行归一化（以q为中心），然后通过MLP网络提取出相对特征 F′。这代表了邻居相对于查询点的几何关系。
步骤 2️⃣：计算注意力权重 w_d
- 为了给查询点的特征增加全局上下文，作者对整个局部块 P 的特征进行最大池化（max-pooling），得到一个全局块特征。
- 将上一步得到的相对特征
F^′和这个全局块特征拼接在一起。 - 将拼接后的特征送入网络，预测出查询点
q和它每一个邻居点之间的相对权重w_d。这个权重代表了每个邻居点的重要性。
步骤3️⃣：生成最终的查询点特征f_q
-
利用计算出的权重
w_d，通过一个加权公式来计算查询点q的最终特征f_q。 -
公式 (2):
f_q=∑_{d=1}^kw_d⋅f_d^′+(1−w_d)⋅f_d公式解读： 这个公式非常巧妙。它使用注意力权重
w_d动态地融合了两种信息：- 邻居点的相对特征 (
f_d^′)。F'=\{f'_d\}_{d=1}^k中f_d'表示第d个邻居相对于查询点q的相对向量特征。 - 邻居点的原始块特征 (
f_d)。F=\{f_d\}_{d=1}^n中f_d表示块中第h个点的原始特征向量。
- 邻居点的相对特征 (
-
这使得
f_q不仅包含了邻域的几何关系，也包含了每个邻居点自身的属性，信息量非常丰富。
有了上面的信息，最终距离预测和训练如下：
距离预测： -
将加权特征
f_q和全局块特征F以及查询点q的坐标拼接起来 -
将这个融合了所有信息的长向量送入一个MLP中，输出预测的点到表面距离
d_l
训练（损失函数）
使用L_1损失函数进行监督，即L_1=|d_l-d_{gt}|
作者通过可视化发现：
- 合理性：通常离查询点越近的点获得权重越大
- 适应性：权重和距离并不是严格的负相关，而是学习到更复杂的几何关系（不懂，怎么看出来的）
🤔实际上这里找的是密集的ground truth，也就是学习的方法里面数据是有密集点云的，也就是类似于考试中的开卷考试一样。所以我依照这个稠密点云可以学习到一个表面。
那么这个模型是否对于camel/elephant等是通用的呢？这个就是泛化能力了，模型不是在教这个是中文那个是英文，而是学习a、b、c等，放在这里就是再学习“一个平坦的平面”还是“一个尖锐的棱边”还是说是“一个光滑的曲面呢
学习连续场
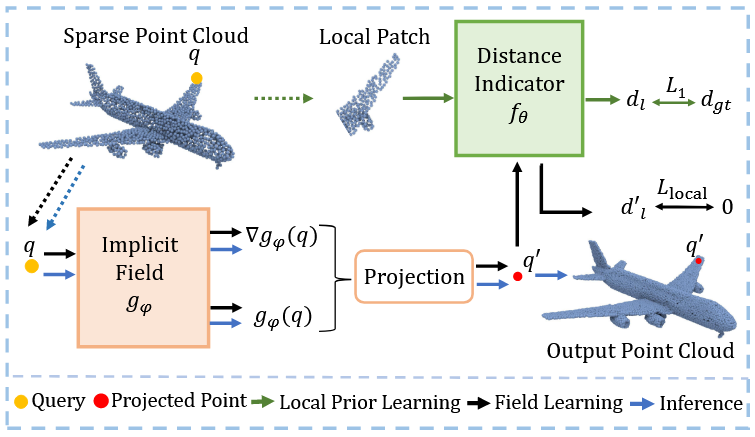
现在再来看看这个图，LDI训练好了之后我们可以把它当黑盒了，那么这里输入和输出是什么？
输入：查询点q和局部patchP
输出：一个标量[1]，为d_l表示这个点到patchP潜在连续表面的距离。
图中的上半部分就是前面LDI如何学习的部分了，接下来讲述第二部分如何学习连续场。
现在我们的目标就是学习一个全局隐式场网络g_\phi。目标就是输入空间中任意一个查询点q我们就可以预测出该点到物体表面的距离d_g。因为并不知道具体精确值是多少，这里就要用到之前的LDI。
流程：
- 全局网络
g_\phi对于查询点q做出预测，根据如下公式进行投影到表面点q'（投影最近的）
MARKDOWN_HASH58859d93c30e635814dc980ed86e3f84MARKDOWNHASH
q'=q-g\phi\dfrac{\nabla g\phi}{\Vert g\phi(q)\Vert_2}
$$
我的理解就是g_\phi就是距离，分数那就是方向（梯度、法向）
刚开始表面点不一定是真的表面，但是通过训练可以获得
-
将这个结果
q'给LDI进行审查 -
LDI判断
q'距离局部真实表面有多远，给出距离值f_\theta(q',P_{q'}) -
如果
g_\phi是正确的，那么距离值就是0,否则就去训练（通过损失函数），损失函数
L_{local}=|f_\theta(q',P_{q'})|
为了让g_\phi更好的学习，还加入了三个辅助的损失项，打包成L_{global}
- 最近点约束
L_{np}：最初可能会投影到很离谱的地方，q'不能离原始稀疏点云中某个点q_s太远
MARKDOWN_HASH58859d93c30e635814dc980ed86e3f84MARKDOWNHASH
L{np}=\Vert q'-q_s\Vert
$$
- 表面点约束
L_{surf}：原始的所有点输入到g_\phi都应该输出是
MARKDOWN_HASH58859d93c30e635814dc980ed86e3f84MARKDOWNHASH
L{serf}=|g_\phi(s_i)|
$$
- 最短距离约束
L_{sp}：技术型约束，用于更好学习距离场，修正梯度方向可能存在的微小误差，尤其是离表面很近的区域
MARKDOWN_HASH58859d93c30e635814dc980ed86e3f84MARKDOWNHASH
L{sp}=|g_\phi(q)|
$$
写到这里差不多就结束了，唯一还需要明白的地方就是上面这个L_{sp}，再来多说一下
投影公式[q' = q - gφ(q) * [单位梯度向量]这个有效的前提是梯度方向能够准确指向离q最近的表面。
但是神经网络只是近似，并不准确。
一种情况：对于一个点
q，它的预测距离很准确，但是梯度方向确实歪的。结果恰好也落在了旁边正确的表面上，其他的损失函数都是最小的（对的），但实际上这并不正确。这会导致细节不正确。
那么我们预测的距离也要最小
- 但不能让都等于0，那不就是自己了吗？
L_{local}进行惩罚 - 所以就是
L_{local}和L_{sp}都小，找到一个平衡点
总而言之这个L_{sp}就像一个拉力，不断把距离场往靠近。其实最好的理解就是中学阶段的点到直线的距离，相同距离的情况下常常会有两个交点，但是我找到最短的距离，就只有一个交点，梯度也是正确的。
写在最后
这个作者Shujuan Li（谷歌学术🔗：Shujuan Li - THU）有点厉害，一个隐式场做了4篇A的成果还有一个在投。有机会都学习一下！
