04-典型的凸优化问题

1 凸优化问题

凸优化问题

标准形式的凸优化问题


\begin{array}{ll}
\min _{x \in D} & f(x) \\
\text { s.t. } & g_i(x) \leq 0, \quad i=1, \ldots, m \\
& A x=b
\end{array}

目标函数f、不等式约束条件g_i都是凸函数，必须是Ax=b
定义域D=\text{dom }f\cap (\cap_{i=1}^m\text{dom }g_i)通常省略
可行域为X=D\cap\{x\mid g_i(x)\leq 0,i=1,2,\cdots,m,Ax=b\}

注意定义域和可行域的区别。可行域是定义域交上约束条件的集合。

--------------
argmin：

f^*=\min_x f(x)
x^*=\operatorname*{argmin}_x f(x)
表示在f(x)取到最小值的时候x的值
-------------

若X_{\text{opt}}为下面凸优化问题的解集，即


\begin{align}
X_{\text{opt}}=\operatorname*{argmin}_x\quad &f(x)\\
\text{s.t.}\quad &g_i(x)\leq 0,\quad i=1,...,m\\
&Ax=b
\end{align}

其中X_{\text{opt}}是凸集.

--------------------------------------------
证明：若x,y是凸优化问题的解，则f(x)=f(y)=f^*。对于任意的0\leq t\le 1，有g_i(tx+(1-t)y)\leq tg_i(x)+(1-t)g_i(y)\leq 0，即A(tx+(1-t)y)=tAx+(1-t)Ay=b ，得到f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)=f^*。所以tx+(1-t)y也是凸优化问题的解，得证
--------------------------------------------

若f是严格凸函数，则凸优化问题的解唯一，即X_\text{opt}只有一个元素

------------------------------------------

局部和全局最优

凸优化问题的任意局部最优解都是全局最优解

证明采用反证法证明矛盾

可微凸优化问题的最优性条件

x是凸优化问题\min_{x\in X} f(x)的最优解当且仅当x可行且满足：


\nabla f(x)^\top(y-x)\geq 0,\quad \forall y\in X.

我的理解：在这个可行域内任何一个方向都和正梯度方向呈锐角或直角（大于等于0），也就是无法再下降

几何解释：与-\nabla f(x)（负梯度）呈锐角的方向都是下降方向。任取y\in X，-\nabla f(x)与y-x呈钝角，即内积 \langle y-x,-\nabla f(x)\rangle \leq 0.提出一个负号即是上式。若存在y\in X使得-\nabla f(x)与y-x呈锐角，那说明还能够继续下降，在可行域X还能找到比x更优的解。

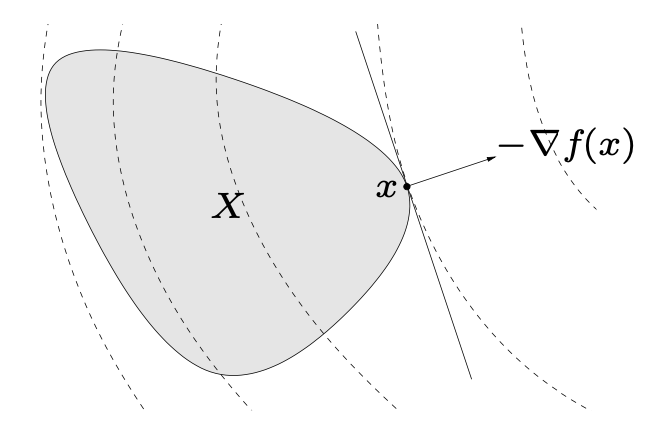
如果\nabla f(x)非零，它定义了可行域X在x处的支撑超平面，即再也无法下降。

具体含义

无约束优化：x是最优解当且仅当


x\in \text{dom }f,\quad \nabla f(x)=0

--------------
证明：取y=x-t\nabla f(x),t\gt 0，可得\nabla f(x)^\top (y-x)=-t\Vert \nabla f(x)\Vert_2^2 \geq 0，所以\nabla f(x)=0
-------------

等式约束优化问题：


\min_x \quad f(x) \quad \text{ s.t.}  \quad Ax=b

x是最优解当且仅当存在v使得


x\in \text{dom } f,\ Ax=b,\ \nabla f(x)+A^\top v=0

注意这里的A


A=\begin{pmatrix}
a_1^\top  \\
a_2^\top  \\
\vdots \\
a_n^\top 
\end{pmatrix},A^\top=(a_1,a_2,\cdots,a_n)\\
\nabla f(x)=A^Tv=\sum_{i=1}^n a_i\cdot v_i

非负约束优化问题：


\min_x \quad f(x) \quad \text{s.t.}  \quad x\geq 0

x是最优解当且仅当


x\in \text{dom }f,\quad x\geq 0,\quad 
\begin{cases}
\nabla f(x)_i\geq 0 &x_i=0\\
\nabla f(x)_i=0&x_i>0
\end{cases}

2 线性规划

线性规划基本形式

线性规划问题一般形式如下：


\begin{align}
\min_{x\in\mathbb{R}^n}\quad  &c^\top x\\
\text{s.t.}\quad &Ax=b\\
&Gx\leq e
\end{align}\tag{1}

标准形式


\begin{align}
\min_{x\in\mathbb{R}^n}\quad  &c^\top x\\
\text{s.t.}\quad &Ax=b\\
&x\geq 0
\end{align}\tag{2}

不等式形式


\begin{align}
\max_{y\in\mathbb{R}^n}\quad  &b^\mathsf{T}y\\
\text{s.t.}\quad &A^\mathsf{T}y\leq c\\

\end{align}\tag{3}

基追踪问题

基追踪问题是压缩感知中的一个基本问题，可以写为


\begin{align}
\min_{x\in\mathbb{R}^n}\quad  &\Vert x\Vert_1\\
\text{s.t.}\quad &Ax=b\\
\end{align}\tag{4}

对于每一个|x_i|引入一个新的变量z_i，可以将上述凸问题转化为


\begin{align}
\min_{x\in\mathbb{R}^n}\quad  &\sum_{i=1}^nz_i\\
\text{s.t.}\quad &Ax=b\\
&-z_i\leq x_i\leq z_i,\quad i=1,2,\cdots,n,
\end{align}\tag{5}

这是一个线性规划问题

这里使用到了


\begin{align}
\Vert x\Vert&=\sum|x_i|\\
z_i&=|x_i|\\
0\leq &|x_i|\leq z_i
\end{align}

（待完成引入正负）

数据拟合

(这里有一个伪逆的概念)


\begin{align}
&\min_x\Vert Ax-b\Vert_2\\
x&=A^\top b\\
A^\top Ax&=A^\top b\\
x&=(A^\top A)^{-1}A^\top b
\end{align}

在数据拟合中，除了常用的最小二乘模型外，还有最小\ell_1范数模型


\min_{x\in\mathbb{R}^n}\quad \Vert Ax-b\Vert_1\tag{6}

和最小\ell_\infty范数模型


\min_{x\in\mathbb{R}^n}\quad \Vert Ax-b\Vert_\infty\tag{7}

这两个问题都可以转化为线性规划的形式.

对于\ell_1（问题6）通过引入变量y=Ax-b，可以得到如下等价问题：


\begin{array}{r l}{\underset{x,y\in\mathbb{R}^{n}}{\mathrm{min}}}&{{}\|y\|_{1},}\\ {x,y\in\mathbb{R}^{n}}&{{}}\\ {\mathbf{s.t.}}&{{}y=A x-b.}\end{array}

对于\ell_\infty（问题7），令t=\Vert Ax-b\Vert_\infty，则得到等价问题


\begin{align}
\min_{x\in\mathbb{R}^n,t\in\mathbb{R}}\quad &t\\
\text{s.t.}\quad &\Vert Ax-b\Vert_\infty\leq t
\end{align}

利用\ell_\infty范数的定义，由于


\begin{align}
|(Ax-b)_i|&\leq t\\
-t\mathbf{1}\leq Ax-b&\leq t\mathbf{1}
\end{align}

其中\mathbf{1}表示全1的向量

可以进一步写为

（未完成）

二次规划

二次规划问题


\begin{align}
\min_x\quad &\frac{1}x^\top Px+q^\top x+r\\
\text{s.t.}\quad &Gx\leq h\\
&Ax=b
\end{align}\tag{11}

P\in S_{+}^{n}，即P是半正定的，故目标函数是二次的. 若P不是半正定的，则该优化问题不是凸的.
在一个多面体内最小化一个二次凸函数

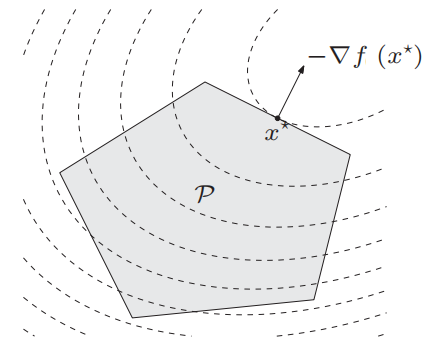
二次规划的标准形式


\begin{align}
\min_x\quad &\frac{1}x^\top Px+q^\top x\\
\text{s.t.}\quad &x\geq 0\\
&Ax=b
\end{align}\tag{12}

所有二次规划问题都可以写成标准形式

半定规划

半定规划问题的一般形式如下：


\begin{align}
\min_x\quad &c^\top x,\\
\text{s.t.}\quad &x_1A_1+x_2A_2+\cdots+x_nA_n+B\preceq 0,\\
&Gx=h
\end{align}\tag{13}

A\succeq B\\
A-B\succeq 0
即A-B半正定，A-B\geq 0是每一项都大于等于（逐元素）

类似与线性规划问题，我们考虑半正定规划的标准形式


\begin{array}{ll}
\min _{X} & \langle C, X\rangle, \\
\text { s.t. } & \left\langle A_{1}, X\right\rangle=b_{1}, \\
& \cdots \\
& \left\langle A_{m}, X\right\rangle=b_{m}, \\
& X \succeq 0 .
\end{array}\tag{14}

形如(13) 式的优化问题都可以转化成(14) 式的形式


\begin{align}
\langle x,y\rangle&=x^\top y\\
\langle C,X\rangle&=\mathrm{tr}(C^\top X)\\
&=\sum_{ij}C_{ij}X_{ij}
\end{align}

二次约束二次规划问题的半定规划松弛

考虑二次约束二次规划问题


\begin{array}{l l l}{\underset{x\in\mathbb{R}^{n}}{\operatorname*{min}}}&{x^{\mathrm{T}}A_{0}x+2b_{0}^{\mathrm{T}}x+c_{0},}\\ {\mathrm{s.t.}}&{x^{\mathrm{T}}A_{i}x+2b_{i}^{\mathrm{T}}x+c_{i}\le0,}&{i=1,2,\cdots,m,}\end{array}\tag{15}

注意X,X^\top,A的trace按照顺序从任意一项开始都行，例如


x^\top A x=\mathrm{Tr}(x^\top Ax)=\mathrm{Tr}(xx^\top A)=\mathrm{Tr}( Axx^\top)=\langle A,xx^\top\rangle

写出问题(15)的半定规划松弛问题.对任意x\in\mathbb{R}^n以及A\in\mathcal{S}^n，有恒等式


x^{\mathrm{T}}A x=\mathrm{Tr}(x^{\mathrm{T}}A x)=\mathrm{Tr}(A x x^{\mathrm{T}})=\left\langle A,x x^{\mathrm{T}}\right\rangle

因此问题（15）中所有的二次项均可用下面的方式进行等价刻画：


\begin{array}{r}{x^{\mathrm{T}}A_{i}x+2b_{i}^{\mathrm{T}}x+c_{i}=\langle A_{i},x x^{\mathrm{T}}\rangle+2b_{i}^{\mathrm{T}}x+c_{i}.}\end{array}

由上述分析，原始问题等价于


\begin{array}{r l}{\underset{x\in\mathbb{R}^{n},X}{\mathrm{min}}}&{{}\langle A_{0},X\rangle+2b_{0}^{\mathrm{T}}x+c_{0}}\\ {\mathrm{\mathbf{s.t.}}~}&{{}\langle A_{i},X\rangle+2b_{i}^{\mathrm{T}}x+c_{i}\le0,\quad i=1,2,\cdots,m,}\\ &{X=x x^{\mathrm{T}}.}\end{array}\tag{16}

进一步地，


\begin{aligned}
x^{\mathrm{T}} A_{i} x+2 b_{i}^{\mathrm{T}} x+c_{i} & =\left\langle\left(\begin{array}{cc}
A_{i} & b_{i} \\
b_{i}^{\mathrm{T}} & c_{i}
\end{array}\right),\left(\begin{array}{cc}
X & x \\
x^{\mathrm{T}} & 1
\end{array}\right)\right\rangle, \\
& \xlongequal{\text { def }}\left\langle\overline{A_{i}}, \bar{X}\right\rangle, \quad i=0,1, \cdots, m .
\end{aligned}

接下来将等价问题(16) 松弛为半定规划问题．

在问题（16）中，唯一的非线性部分是约束X=xx^\mathsf{T}，我们将其松弛称半正定约束X\succeq x x^{\mathrm{T}}.可以证明，\overline{{X}}\succeq0与X\succeq x x^{\mathrm{T}}是等价的。
因此这个问题的半定规划松弛可以写成


\begin{array}{r l}{\underset{X}{\operatorname*{min}}}&{{}\langle A_{0},X\rangle}\\ {\mathrm{s.t.}}&{{}\langle \overline{A_{i}},\overline{{X}}\rangle\le0,\quad i=1,2,\cdots,m,}\\ {\mathrm{s.t.}}&{{}\overline{{X}}\succeq0,}\\ &{\overline{{X}}_{n+1,n+1}=1.}\end{array}

其中“松弛”来源于我们将X=xx^\mathsf{T}替换成了X\succeq xx^\mathsf{T}

极小化最大特征值


\begin{align}
f(y)&\approx f(x)+\nabla f(x)^\top(y-x)+\frac{1}{2}(y-x)^\top H(y-x)\\
&\leq f(x)+\nabla f(x)^\top (y-x)+\frac{t}{2}\Vert y-x\Vert_2^2 \lambda_\max(H)\\
&\Vert \nabla f(x)\Vert_2^2+\langle \nabla f(x),y-x\rangle+\frac{t}{2}\Vert y-x\Vert _2^2\\
&\Vert y-x +k\nabla f(x)\Vert_2^2\Rightarrow y=x-k\nabla f(x)
\end{align}