03-凸函数

3.1 基础知识

梯度

梯度的定义：

给定函数f:\mathbb{R}^n\rightarrow\mathbb{R}，且f再点x的一个邻域内有意义，若存在向量g\in\mathbb{R}^n满足：

\lim_{p\rightarrow 0}\frac{f(x+p)-f(x)-g^T p}{\Vert p\Vert}=0

其中\Vert \cdot\Vert是任意向量范数，就称f在点x处可微.此时g称为f在点x处的梯度，记作\nabla f(x)

若f在点x处梯度存在，在定义式中令p=\varepsilon e_i，e_i是第i个分量为1的单位向量（其余是），可知\nabla f(x)的第i个分量\frac{\partial f(x)}{\partial x_i}.因此，

\nabla f(x)=\left[\frac{\partial f(x)}{\partial x_{1}}, \frac{\partial f(x)}{\partial x_{2}}, \cdots, \frac{\partial f(x)}{\partial x_{n}}\right]^{\mathrm{T}}

海瑟矩阵

二阶偏导数\frac{\partial^2f(x)}{\partial x_i\partial x_j}

\nabla^2 f(x) = 
\begin{bmatrix}
\frac{\partial^2 f(x)}{\partial x_1^2} & \frac{\partial^2 f(x)}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f(x)}{\partial x_1 \partial x_n} \\
\frac{\partial^2 f(x)}{\partial x_2 \partial x_1} & \frac{\partial^2 f(x)}{\partial x_2^2} & \cdots & \frac{\partial^2 f(x)}{\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f(x)}{\partial x_n \partial x_1} & \frac{\partial^2 f(x)}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f(x)}{\partial x_n^2}
\end{bmatrix}

矩阵变量函数的导数

在实际应用中，矩阵Fréchet可微往往比较繁琐，所以我们用Gâteaux 可微：

定义（Gâteaux 可微）

设f(X)为矩阵变量函数，如果对任意方向V\in\mathbb{R}^{m\times n}，存在矩阵G\in\mathbb{R}^{m\times n}满足：

\lim_{t\rightarrow 0}\frac{f(X+tV)-f(X)-t\langle G,V\rangle}{t}=0

则称f关于X是Gâteaux 可微的。

当f是Fréchet 可微函数时，f也是Gâteaux 可微的，且这两种意义下的梯度相等。

线性函数：f(X)=\mathrm{tr}(AX^\top B)

\begin{align*}
\lim_{t \to 0} \frac{f(X + tV) - f(X)}{t} &= \lim_{t \to 0} \frac{\text{tr}(A(X + tV)^\top B) - \text{tr}(AX^\top B)}{t} \\
&=\lim_{t\rightarrow 0}\frac{\text{tr}(A(X^\top+tV^\top)B)-\text{tr}(AX^\top B)}{t}\\
&=\lim_{t\rightarrow 0}\frac{\text{tr}(AX^\top B)+t\text{tr}(AV^\top B)-\text{tr}(AX^\top B)}{t}\\
&= \text{tr}(AV^\top B) = \text{tr}(V^\top BA)=\langle BA, V \rangle.
\end{align*}

因此，\nabla f(X)=BA

3.2 凸函数的定义与性质

凸函数定义：函数f: \mathbb{R}^n\rightarrow \mathbb{R}，若\mathrm{dom} f是凸集，且

f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta)f(y)

对所有的x,y\in\mathrm{dom} f,0\leq \theta \leq 1都成立，则称f是凸函数

几何表现：任意两点的连线都在其的上方，就是凸函数

定义域是凸集（一定要注意）

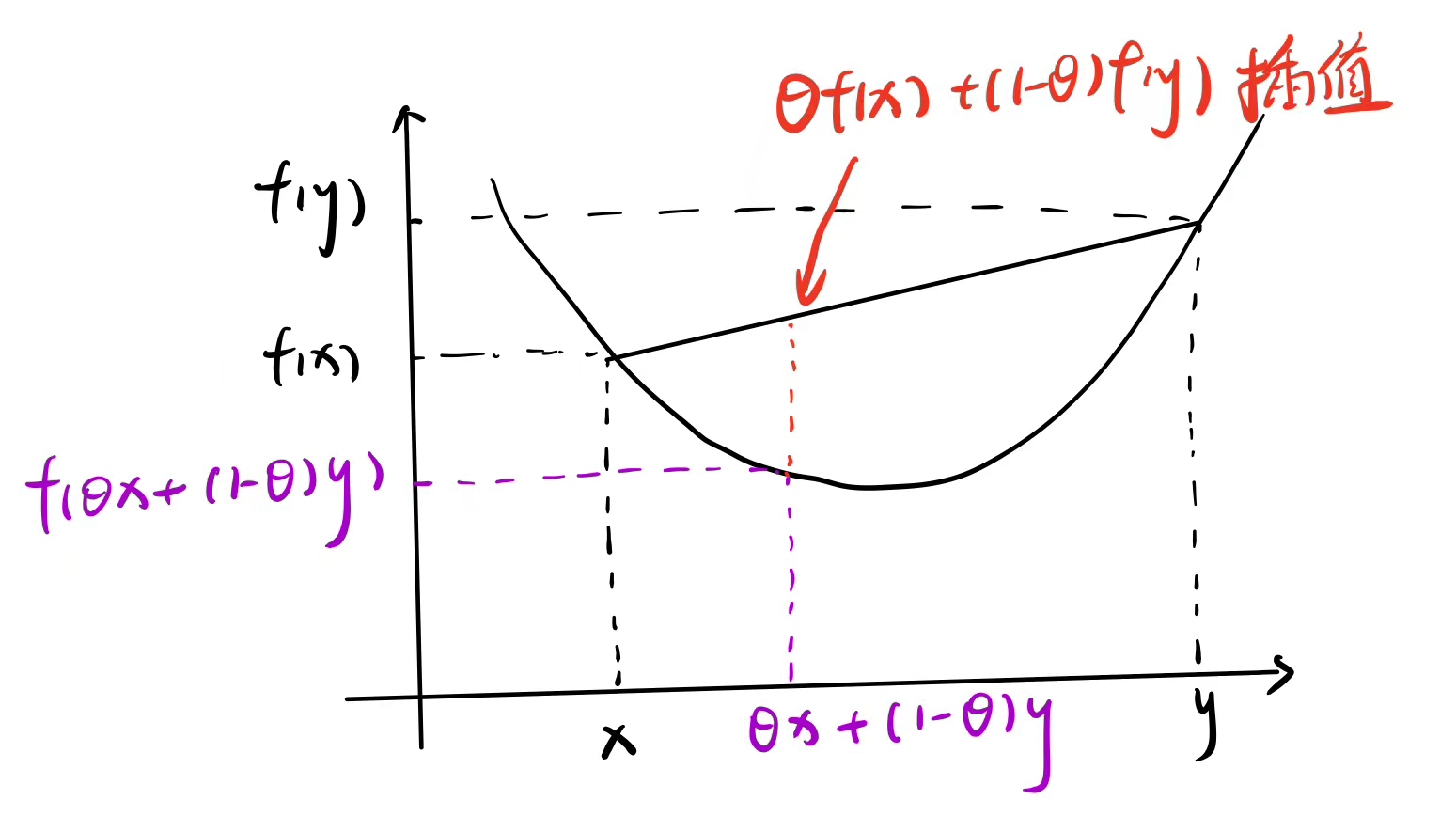
如果不取到端点的话就是严格凸函数

多元函数的例子

所有的仿射函数既是凸函数，又是凹函数（与一元函数一样）

所有的范数都是凸函数（零范数不是真的范数）

欧氏空间\mathbb{R}^n的例子：

• 仿射函数：f(x)=a^Tx+b
• 范数：\Vert x\Vert _p=(\sum _{i=1}^n |x_i|)^{1/p}(p\geq 1)

矩阵空间\mathbb{R}^{m\times n}的例子

• 仿射函数：

f(X)=\mathrm{tr}(A^T X)+b=\sum_{i=1}^m\sum_{j=1}^n A_{ij}X_{ij}+b

强凸函数

减去一个球（凸函数）还是凸函数那就是强凸函数

• 定义1：若存在常数m>0，使得：

  g(x)=f(x)-\frac{m}{2}\Vert x\Vert ^2

为凸函数，则称f(x)为强凸函数，其中m为强凸参数，称f(x)为m-强凸函数

• 定义2：若存在常数m \gt 0，使得对任意x,y\in \text{dom }f以及\theta\in (0,1)，有

  f(\theta x+(1-\theta y)) \leq \theta f(x)+(1-\theta) f(y)-\frac{m}{2} \theta(1-\theta)\|x-y\|^2

则称f(x)为强凸函数，其中m为强凸参数

• 设f为强凸函数且存在最小值，则f的最小值点唯一

凸函数判定定理

定理

f: \mathbb{R}^n \to \mathbb{R} 是凸函数，当且仅当对每个 x \in \text{dom} f, v \in \mathbb{R}^n，函数 g: \mathbb{R} \to \mathbb{R} 是关于 t 的凸函数

g(t) = f(x + tv), \quad \text{dom} \, g = \{ t \mid x + tv \in \text{dom} \, f \}

一阶条件

定理

一阶条件：对于定义在凸集上的可微函数f，f是凸函数当且仅当

f(y)\geq f(x)+\nabla f(x)^T(y-x) \quad \forall x,y\in\text{dom} f.

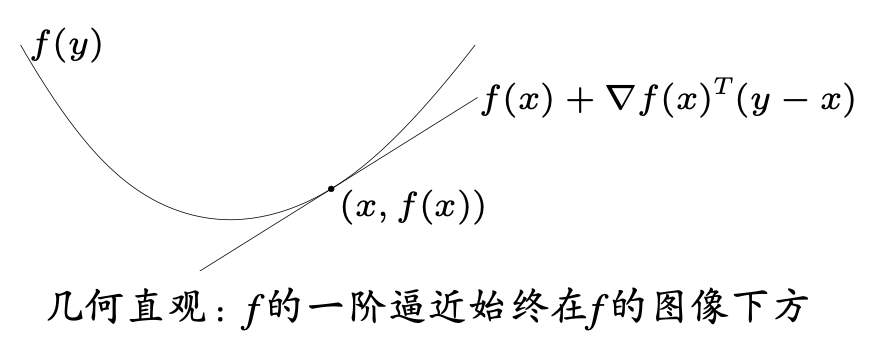
f(x)+\nabla f(x)^T(y-x)为一阶泰勒展开

在二维的情况下，可以认为在任何一点点作其的切线，都在图像的下方，泰勒展开以前都是针对一维变量x展开的，此时的x可以作为矩阵

梯度的单调性

定理

设f为可微函数，则f为凸函数当且仅当\text{dom} f为凸集且\nabla f为单调映射，

(\nabla f(x)-\nabla f(y))^\text{T}(x-y)\geq 0,\quad \forall x,y\in\text{dom}f

类似于(f(x)-f(y))(x-y)\geq 0，可以写出内积形式\langle \nabla f(x)-\nabla f(y),x-y\rangle \geq 0

二阶条件

定理

二阶函数：f在凸集上二阶可微

• f是凸函数当且仅当，海瑟矩阵半正定，即\nabla ^2f(x)\succeq 0
• 如果\nabla ^2f(x)\succ 0则f是严格凸函数
• （如果是f是严格凸函数，但是不能说其半正定，例如f(x)=x^4，但是f^{''}(x)=12x^2在处是等于的）

二次函数f(x)=(1/2)x^TPx+q^Tx+r，那么\nabla f(x)=Px+q,\quad \nabla^2f(x)=P

最小二乘函数：f(x)=\Vert Ax-b\Vert_2^2

\nabla f(x)=2A^T(Ax-b),\quad \nabla^2f(x)=2A^TA

quadratic-over-linear函数：f(x,y)=\frac{x^2}{y}是区域\{(x,y)\mid y>0\}上的凸函数

证明：

\nabla^2 f(x, y) = \frac{2}{y^3} 
\begin{bmatrix}
y \\
-x
\end{bmatrix}
\begin{bmatrix}
y & -x
\end{bmatrix}^T \succeq 0

如何证明

\begin{bmatrix}
y \\
-x
\end{bmatrix}
\begin{bmatrix}
y & -x
\end{bmatrix}^T

是半正定矩阵，即需要证明在z_1,z_2任意的情况下，其值都大于等于，即：

\begin{align}
\begin{bmatrix}
z_1 & z_2
\end{bmatrix}
\begin{bmatrix}
y \\
-x
\end{bmatrix}
\begin{bmatrix}
y & -x
\end{bmatrix}^T
\begin{bmatrix}
z_1 \\ z_2
\end{bmatrix}
&=
\begin{bmatrix}
z_1 & z_2
\end{bmatrix}
\begin{bmatrix}
y^2 & -xy \\
xy & y^2
\end{bmatrix}
\begin{bmatrix}
z_1 \\ z_2
\end{bmatrix}

\\
&=
\begin{bmatrix}
y^2z_1+xyz_2 & -xyz_1+z_2y^2 
\end{bmatrix}
\begin{bmatrix}
z_1 \\ z_2
\end{bmatrix}\\
&=(y^2z_1+xyz_2)z_1+(-xyz_1+z_2y^2)z_2\\
&=(z_1^2+z_2^2)y^2 \geq 0
\end{align}

Jensen不等式

基础Jensen不等式：设f是凸函数，则对于0\leq \theta\leq 1，

f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta)f(y)

概率Jensen不等式：设f是凸函数，则对任意随机变量z

f(\mathbf{E} z) \leq \mathbf{E} f(z)

3.3 保凸的运算

保凸的运算

验证一个函数f是凸函数的方法：

1. 用定义验证（通常将函数限制在一条直线上）
2. 利用一阶条件、二阶条件
3. 说明f可由凸函数的保凸运算得到
   • 非负加权和
   • 与仿射函数的复合
   • （待完成）

非负加权和与仿射函数的复合

若f是凸函数：

• \alpha f是凸函数，其中\alpha \geq 0
• f_1+f_2是凸函数
• f(Ax+b)是凸函数

逐点取最大值

若f_1,\cdots,f_m是凸函数，则f(x)=\max \{f_1(x),\cdots, f_m(x)\}是凸函数

例：

• 分段线性函数：f(x)=\max_{i=1,...,m}(a_i^\top x+b_i)是凸函数

逐点取上界

对于每个y\in\mathcal{A},f(x,y)是关于x的凸函数，则

g(x)=\sup _{y\in\mathcal{A}}f(x,y)

是凸函数

仿射函数的上界保持凸性，f(x,y)的既是不是仿射，只要是凸函数仍然保持凸性

例

• 集合C的支撑函数：S_C(x)=\sup_{y\in C}y^Tx是凸函数

• 集合C点到给定点x的最远距离：

  f(x)=\sup_{y\in C}\Vert x-y\Vert

• 对称矩阵X\in\mathbb{S}^n的最大特征在

  \lambda_\max (X)=\sup_{\Vert y\Vert_2=1}y^TXy

对于任意y固定，f(x)都是关于x的仿射函数，仿射函数取上界也是凸函数

这里有对于inf（下确界）和sup（上确界）的理解

例子：

1. \inf \{1,2,3\}=1
2. \inf\{x\in\mathbb{R},0\lt x\lt 1\}=0 这里可以看出，与取不取得到无关
3. \inf \{(-1)^n+\frac{1}{n}\mid n=1,2,\cdots\}=-1，下确界可以不属于这个集合

与下确界对偶的概念当然是上确界sup

例子：

1. \sup \{1,2,3\}=3
2. \sup \{x \in \mathbb{R}, 0\lt x\lt 1\}=\sup \{x \in \mathbb{R}, 0 \leq x \leq 1\}=1
3. \sup \left\{(-1)^n-\frac{1}{n}: n=1,2,3, \ldots\right\}=1
4. \sup \{a+b: a \in A \operatorname{and} b \in B\}=\sup (A)+\sup (B)

扩展函数

有f(x),x\in \text{dom} f，拓展函数为

\tilde{f}(x) =
\begin{cases}
f(x), & x \in \text{dom}f, \\
+\infty, & x \notin \text{dom}f.
\end{cases}

与标量函数的复合

给定函数g: \mathbb{R}^n\rightarrow \mathbb{R}和h:\mathbb{R}\rightarrow \mathbb{R}，

f(x)=h(g(x))

若

• g是凸函数，h是凸函数，h单调不减
• g是凹函数，h是凸函数，h单调不增

那么f是凸函数

对于n=1，g,h都可微分的情况，给出简证

f^{\prime\prime}(x)=h^{\prime\prime}(g(x))g^\prime(x)^2+h^\prime(g(x))g^{\prime\prime}(x).

要使得f^{\prime\prime}(x)\geq 0，那么需要每一项都大于等于，充分条件为：

• h^{\prime\prime}(g(x))\geq 0,h^\prime(g(x))\geq 0,g^{\prime\prime}(x)\geq 0
• h^{\prime\prime}(g(x))\geq 0,h^\prime(g(x))\leq 0,g^{\prime\prime}(x)\leq 0

那么则分别对应两种情况

• h为凸函数，h不递减，g为凸函数
• h为凸函数，h不递增，g为凹函数

g,h不可微分的时候，结论依然成立

推论：

• 如果g是凸函数，则\exp g(x)是凸函数
• 如果g是正值凸函数，则1/g(x)是凸函数

与向量函数的复合

给定函数g:\mathbb{R}^n\rightarrow \mathbb{R}^k和h:\mathbb{R}^k\rightarrow \mathbb{R}

f(x)=h(g(x))=h(g_1(x),g_2(x),\cdots,g_k(x))

与「标量函数的复合」类似，只不过拓展到h关于每个分量都单调不减/不增

推论

• 如果g_i是正值凹函数，则\sum_{i=1}^m\log g_i(x)是凹函数
• 如果g_i是凸函数，则\log \sum_{i=1}^m\exp g_i(x)是凸函数

取下确界

若f(x,y)关于(x,y)整体是凸函数，C是凸集，则

g(x)=\inf_{y\in C}f(x,y)

是凸函数

例子

考虑函数f(x,y)=X^TAx+2x^TBy+y^TCy，海瑟矩阵满足

\begin{bmatrix}
A & B\\B^T & C
\end{bmatrix}
\succeq 0,\quad C\succ 0

则f(x,y)为凸函数，对y求最小值得

\frac{\partial f(x,y)}{\partial y}=2B^Tx+2Cy=0\\
\begin{align}
Cy&=-B^Tx \quad (C\succ 0)\\
y^*&=-C^{-1}B^Tx
\end{align}
\\\
g(x)=\inf_y f(x,y)=x^T(A-BC^{-1}B^T)x

因此g是凸函数，进一步地，A的Schur补A-BC^{-1}B^T\succeq 0

点x到凸集S的距离\text{dist}(x,S)=\inf_{y\in S}\Vert x-y\Vert是凸函数

透视函数

定义f:\mathbb{R}^n\rightarrow \mathbb{R}的透视函数g:\mathbb{R}^n\times \mathbb{R}\rightarrow \mathbb{R}，

g(x,t)=tf(x/t),\quad \text{dom}\ g=\{(x,y)\mid x/y\in \text{dom}\ f,t>0\}

若f是凸函数，则g也是凸函数

例子

f(x)=x^Tx是凸函数，因此g(x,t)=x^Tx/t是区域\{ x,t\}\mid t>0\}上的凸函数

t(\frac{x}{t})^T(x/t)=\frac{x^Tx}{t}

共轭函数

函数f的共轭函数定义为

f^*(y)=\sup_{x\in\text{dom}\ f}(y^Tx-f(x))

• f^*恒为凸函数，无论f是否为凸函数

y是给定的，变x取上界

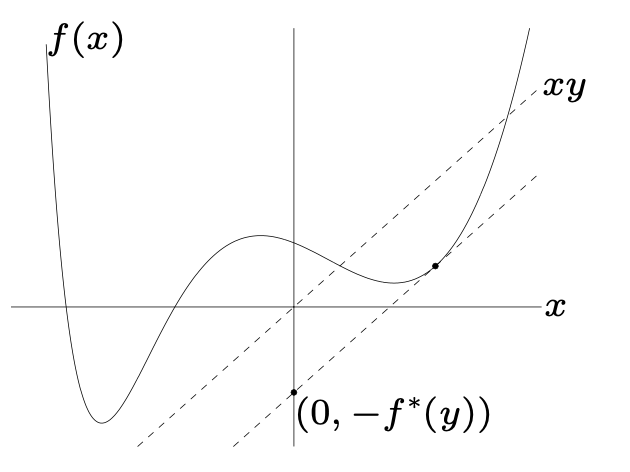
xy水平向下平移，直到与之相切的地方，即求xy与f(x)的切线，即

\frac{\partial xy-f(x)}{\partial x}=0\Rightarrow y-f^\prime(x)=0

例子

• 负对数f(x)=-\log x

\begin{aligned}
f^*(y) & =\sup _{x>0}(x y+\log x) \\
& = \begin{cases}-1-\log (-y) & y<0 \\
\infty & \text { 其他 }\end{cases}
\end{aligned}

过程:当y\lt 0的时候，有

\begin{align}
g(x)&=xy+\log x\\
g^\prime(x)&=y+\frac{1}{x}=0\Rightarrow x=-\frac{1}{y}\\
f^*(y)&=\sup_x (xy+\log x)\\
&=-\frac{1}{y}\cdot y+\log(-\frac{1}{y})\\
&=-1-\log(-y)
\end{align}

• 强凸二次函数f(x)=(1 / 2) x^T Q x, Q \in \mathbb{S}_{++}^n

\begin{aligned}
f^*(y) & =\sup _x\left(y^T x-(1 / 2) x^T Q x\right) \\
& =\frac{1}{2} y^T Q^{-1} y
\end{aligned}

过程有

\begin{align}
g(x)&=y^\top x-\frac{1}{2}x^\top Qx\\
g^\prime(x)&=y-Qx=0\Rightarrow x^*=Q^{-1}y\\
f^*(y)&=\frac{1}{2}y^\top Q^{-1}y-\frac{1}{2}(Q^{-1}y)^\top\\
&=\frac{1}{2}y^\top Q^{-1}y
\end{align}