写在前面
这四题都很有分量,这是我第一次觉得力扣周赛原来这么有含金量,以后又要认真对待一场比赛了。后面三个题是真的好!
比赛链接:第 300 场周赛 - 力扣(LeetCode)
2.螺旋矩阵 IV(模拟题/技巧)
题意

给一个头指针为head的链表,从左上角开始填写螺旋矩阵,如果没有填满则写-1.
思路
模拟题,但是这里有一个技巧是我以前从来没有用的,要我自己写我会写的很麻烦很麻烦,但是y总这个方法就很好。
用一个dx[],dy[]表示上下左右,用d=0,1,2,3表示dx[],dy[]的下标,每次判断如果越界,那么就d = (d+1) % 4就可以完成转向。
int a = x + dx[d], b = y + dy[d];
if (a < 0 || a >= n || b < 0 || b >= m || res[a][b] != -1) {
d = (d + 1) % 4;
a = x + dx[d], b = y + dy[d];
}
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
vector<vector<int>> spiralMatrix(int n, int m, ListNode* p) {
vector<vector<int>> res(n, vector<int>(m, -1));
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int x = 0, y = 0, d = 1;
for (int i = 0; i < n * m && p; i ++ ) {
res[x][y] = p->val;
int a = x + dx[d], b = y + dy[d];
if (a < 0 || a >= n || b < 0 || b >= m || res[a][b] != -1) {
d = (d + 1) % 4;
a = x + dx[d], b = y + dy[d];
}
x = a, y = b;
p = p->next;
}
return res;
}
};
//Author : yxc
3.知道秘密的人数(动态规划+前缀和)
题意
在第 1 天,有一个人发现了一个秘密。
给你一个整数 delay ,表示每个人会在发现秘密后的 delay 天之后,每天 给一个新的人 分享 秘密。同时给你一个整数 forget ,表示每个人在发现秘密 forget 天之后会 忘记 这个秘密。一个人 不能 在忘记秘密那一天及之后的日子里分享秘密。
给你一个整数 n ,请你返回在第 n 天结束时,知道秘密的人数。由于答案可能会很大,请你将结果对 $10^9 + 7$ 取余 后返回。
示例1:
输入:
n = 6,delay = 2,forget = 4
输出:5
解释:
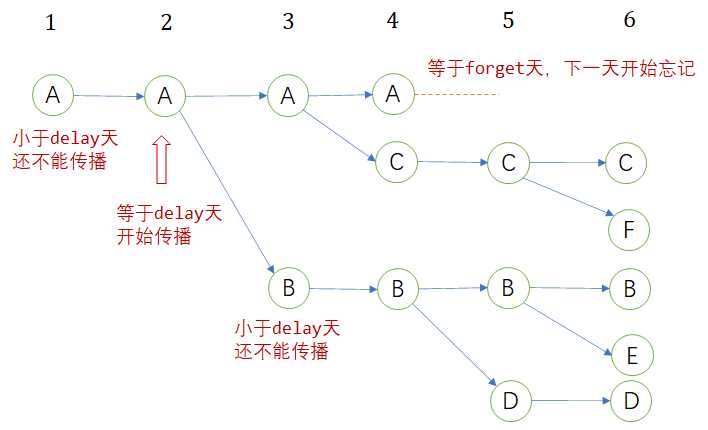
第 1 天:假设第一个人叫 A 。(一个人知道秘密)
第 2 天:A 是唯一一个知道秘密的人。(一个人知道秘密)
第 3 天:A 把秘密分享给 B 。(两个人知道秘密)
第 4 天:A 把秘密分享给一个新的人 C 。(三个人知道秘密)
第 5 天:A 忘记了秘密,B 把秘密分享给一个新的人 D 。(三个人知道秘密)
第 6 天:B 把秘密分享给 E,C 把秘密分享给 F 。(五个人知道秘密)
思路
用f[i][j]原本表示第i天,已经知道秘密第j天的人数个数(集合)。delay<=j<forget
- j>1:
f[i][j] = f[i-1][j-1] - j=1:
f[i][1] = f[i-1][delay] + f[i-1][delay+1] + ... + f[i-1][forget-1]
这样的时间复杂度是$O(n^3)$的,通过上面的式子可以看到可以用前缀和优化,我们用a = delay, b = forget来简化。
所以变成f[i][j]表示第i天,已经知道秘密的前j天的人数个数。
- j>1:
f[i][j] = f[i-1][j-1]-f[i-1][j-2] - j=1:
f[i][1] = f[i-1][b-1] - f[i-1][a-1]
为什么这么思考呢,因为我们可以想到,当新的一天开始,新知道秘密的,也就是j=1的时候的人是哪些?—— 是上一天所有人数可以传播的人的集合,可以传播的指的是delay<=j<forget,所以用前缀和就是pre[b-1]-pre[a-1]。
那么除开第一天又是哪些人呢?f[i][j] (j>1)来看的话,那就是上一天知道秘密在j-1天转移过来的,也就是f[i-1][j-1]这些人新增加一天知道的。
代码
class Solution {
public:
int peopleAwareOfSecret(int n, int a, int b) {
const int MOD = 1e9 + 7;
vector<vector<int>> f(n + 1, vector<int>(n + 1));
for (int i = 1; i <= b; i ++ ) f[1][i] = 1;
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= b; j ++ ) {
if (j == 1) f[i][j] = (f[i - 1][b - 1] - f[i - 1][a - 1]) % MOD;
else f[i][j] = (f[i - 1][j - 1] - f[i - 1][j - 2]) % MOD;
f[i][j] = (f[i][j] + f[i][j - 1]) % MOD;
}
return (f[n][b] + MOD) % MOD;
}
};
//Author : yxc
4.网格图中递增路径的数目(记忆化搜索)
题意
给你一个 m x n 的整数网格图 grid ,你可以从一个格子移动到 4 个方向相邻的任意一个格子。
请你返回在网格图中从 任意 格子出发,达到 任意 格子,且路径中的数字是 严格递增 的路径数目。由于答案可能会很大,请将结果对 $10^9 + 7$ 取余 后返回。
如果两条路径中访问过的格子不是完全相同的,那么它们视为两条不同的路径。
例如:
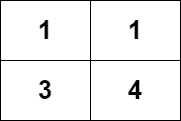
输入:
grid = [[1,1],[3,4]]
输出:8
解释:严格递增路径包括:
· 长度为 1 的路径:[1],[1],[3],[4] 。
· 长度为 2 的路径:[1 -> 3],[1 -> 4],[3 -> 4] 。
· 长度为 3 的路径:[1 -> 3 -> 4] 。
路径数目为 4 + 3 + 1 = 8 。
思路
因为这个路径是严格递增的,所以不会存在环,对于每一个点的路径数等于1+四个方向的方案数。
这个1是因为本身一个点(与四个方向无关),然后我们并不知道每个方向的方案数,所以需要记忆化搜索,这样如果对于点$(x,y)$得到了方案数,下一次就不需要再递归了,只需要返回这个值即可,所以dfs可以这么写:
int dp(int x,int y)
{
if (f[x][y]) return f[x][y];//已经搜过
f[x][y] = 1;//初始是1
for (int i=0;i<4;i++)//四个方向
{
int a = x+dx[i], b = y+dy[i];
if (a>=0&&a<n&&b>=0&&b<m&&g[a][b]>g[x][y])//判断条件
f[x][y] = (f[x][y] + dp(a,b)) % mod;//加上对应方向的方案数
}
return f[x][y];
}
最后再加起来每个点的dp(i,j)即可。
代码
class Solution {
public:
vector<vector<int>> g;
int n,m;
int f[1007][1007];
const int mod = 1e9+7;
int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
int dp(int x,int y)
{
if (f[x][y]) return f[x][y];
f[x][y] = 1;
for (int i=0;i<4;i++)
{
int a = x+dx[i], b = y+dy[i];
if (a>=0&&a<n&&b>=0&&b<m&&g[a][b]>g[x][y])
f[x][y] = (f[x][y] + dp(a,b)) % mod;
}
return f[x][y];
}
int countPaths(vector<vector<int>>& grid) {
n = grid.size(), m = grid[0].size();
g = grid;
int ans = 0;
for (int i=0;i<n;i++)
for (int j=0;j<m;j++)
ans = (ans + dp(i,j)) % mod;
return ans;
}
};
