本场比赛最后压哨绝杀4:59:16过掉1002的搜索成功达到五题,最后成绩在164名,1002罚时太高(被某人演了)...总体来说还是比较满意的,打败了武地的所有队,在本校也排在前三,距离第四还多了三题。希望再接再厉,后天又有一场牛客!
本场手速两题,前两题都是题目只有三十多个队时候出的,还比较快,小小纪念一下:

依旧是按照做题顺序来写的。
1011.Random(签到)
题意:给你$N$个数字,每个都是在$[0,1]$中随机,做$M$次操作,$\frac{1}{2}$几率删除最大值,$\frac{1}{2}$几率删除最小值,求最后剩下数字的和,答案对$10^9+7$取模。
思路:$M$次操作删除一个数,那么最后剩下随机的$N-M$个数,概率又是$\frac{1}{2}$几率删除,期望当然是$\frac{1}{2}$,那么答案就是$\frac{1}{2}\times (N-M)$,注意取模,这里要用到逆元,除以$2$相当于乘以$2^{mod-2}$。
代码:
inline void Case_Test()
{
cin>>n>>m;
int res = n-m;
res = res*qpow(2,mod-2,mod)%mod;
cout<<res<<endl;
}
1012.Alice and Bob(博弈)
题意:一共有$m$个数组在黑板上,现在由Alice进行操作,然后Bob。
- Alice将黑板上的数分成两类
- Bob将黑板中的一类擦掉,另外一类都$-1$
如果最后黑板上有$0$出现,则Alice获胜。否则Bob获胜。
思路:想要Alice赢肯定是需要出现$0$,但是Bob肯定会每次删掉最小的,接近$0$的,例如这时候分成了$[1,5,8],[2,3,6]$,Bob肯定需要删除第一类,如果删除第二类的话,那么第一类$-1$就变成了$[0,4,7]$这样Alice就赢了。
那么这时候Alice想要获得$0$,则需要将$2$个$1$分成不同的两类,比如$[1,5,6],[1,7,8]$这样Bob无论删除那一类,另外一边都会$-1$而得到$0$。
那么如果没有$1$呢?那么我们需要有$4$个$2$,例如$[2,2,5,6],[2,2,8,9]$,这样删除任意一类(例如删除第一类),则剩下了$[1,1,7,8]$,这时候又有了上述的$2$个$1$的情况。
那么如果没有$2$呢,则需要$8$个$3$,以此类推,每次需要多乘以$2$。
这就是博弈论经典的推状态,每次从必胜状态往外推必胜或者必败状态。
那么现在我倒着来,for i = n-1...0,每次将a[i]=a[i+1]/2,每次$2$个$i$可以分成不同的两类,导致可以生成 $1$个$i-1$。
最后再判断是否有$0$即可。
代码:
inline void Case_Test()
{
cin>>n;
for (int i=0;i<=n;i++)
cin>>a[i];
for (int i=n-1;i>=0;i--)
a[i] += a[i+1]/2;
if (a[0])
cout<<"Alice"<<endl;
else
cout<<"Bob"<<endl;
}
1003.Backpack(动态规划)
题意:给你一个容积为$m$的背包,以及$n$个物品,每个物品的容积是$v_i$,价值是$w_i$,求装满时候的最大异或和
数据范围:$1\leq n,m \lt 2^{10},1\leq v_i,w_i \lt 2^{10}$
思路:我的卡时终于派上用场啦!我一开始想各种,比如trie或者线性基等,结果我跟队友讲了一下暴力的想法,然后shuffle+卡时过了,时间是800+ms,std是740ms好像是。
就是纯暴力,对于每一个容积开一个set,存入当前的异或和,可以供下次使用。这是纯暴力的想法,然后我怕有数据卡直接1..n,我就加上了shuffle操作,这个操作是在大一校赛脱老师教我的。
嗯,好吧其实加上shuffle也过了hhh,只不过时间长了点,不过我这个卡时确实不稳定。
当循环判断时间是否达到1000/T-5的时候,例如当T=10的时候,每次达到1000/10-5=95ms的时候break输出。
代码:
int ti = clock();
cin>>n>>m;
int sum1=0,sum2=0;
for(int i=1;i<=n;i++)
{
cin>>a[i].v>>a[i].w;
sum1+=a[i].v;
sum2=sum2^a[i].w;
}
if(sum1==m)
{
cout<<sum2<<endl;
continue;
}
set<int> st[m+1];
st[0].insert(0);
shuffle (a+1, a+1+n, std::default_random_engine(seed));
for(int i=1;i<=n;i++)
{
int v = a[i].v, w = a[i].w;
if (clock()-ti>1000/t-5) break;//卡时,T=10的时候95ms时候break输出
for(int j=m-v;j>=0;j--)
{
for(int x:st[j])
st[j+v].insert(x^w);//很暴力的
}
}
int num=st[m].size();
if(num==0)
cout<<-1<<endl;
else
{
auto it=st[m].end();//end()是空的 并且是排好序的
it--;//需要--
cout<<*it<<endl;
}
PS:
shuffle操作:
在一开始加上unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
然后用的时候shuffle (a+1, a+1+n, std::default_random_engine(seed));
1009.Laser
题意:在二维坐标上给你$n$个点(敌人),你有一个镭射武器可以往四面八方进行扫射(类似于国际象棋中的皇后),问是否能够扫掉所有的敌人。$T$组数据$n$的和不超过$500,000$.
思路:这个题队友做的,我当时在做搜索,这里先选取两个不在同一条线(指横竖斜)的点,这样可以确定十二个答案来使其扫到,所以答案肯定出现在这十二个点中(因为肯定需要满足扫到这两个点),这十二个点需要一个个去判断是否能消灭其他点,时间复杂度为$O(12\times n)$。
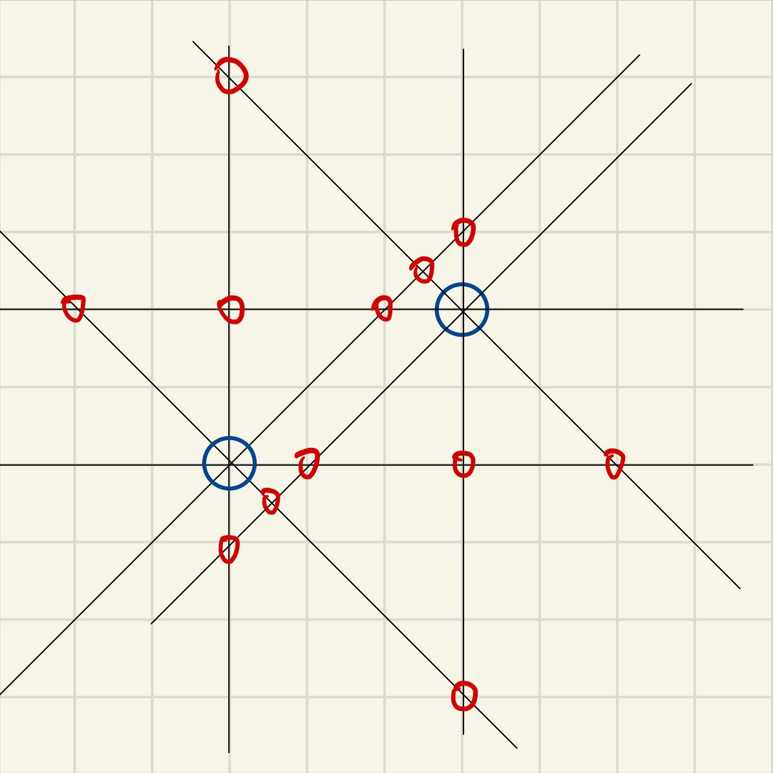
蓝色的点就是我找的两个点(没有横竖斜的线能穿过),这样能够找出潜在的$12$个答案。
然后枚举$12$次对于其他的点进行判断,是否能够超过即可。
代码:
cin>>n;
vector<P> a(n);
for(int i=0;i<n;i++)
cin>>a[i].f>>a[i].s;
bool flag=true;
int aa=a[0].f,bb=a[0].s,x,y;
for(int i=1;i<n;i++)
{
if(a[i].s==a[0].s||a[i].f==a[0].f||abs(a[i].s-a[0].s)==abs(a[i].f-a[0].f))
continue;
else
{
// cout<<i<<endl;
flag=false;
x=a[i].f;
y=a[i].s;
}
}
if(flag)
{
cout<<"YES"<<endl;
continue;
}
else
{
vector<P> point;
point.emplace_back(aa-y+bb,y);
point.emplace_back(x+y-bb,bb);
point.emplace_back(aa,y+x-aa);
point.emplace_back(x,bb-x+aa);
point.emplace_back(x,x-aa+bb);
point.emplace_back(aa,aa-x+y);
point.emplace_back(aa,y);
point.emplace_back(x,bb);
point.emplace_back(aa+y-bb,y);
point.emplace_back(x-y+bb,bb);
if((x-y+bb+aa)%2==0&&(aa-x+y+bb)%2==0)
point.emplace_back((x-y+bb+aa)/2,(aa-x+y+bb)/2);
if((x+aa+y-bb)%2==0&&(x-aa+bb+y)%2==0)
point.emplace_back((x+aa+y-bb)/2,(x-aa+bb+y)/2);
vector<int> vis(point.size(),0);
for(int i=0;i<n;i++)
{
for(int j=0;j<point.size();j++)
{
int xx=point[j].f,yy=point[j].s;
if(a[i].s==yy||a[i].f==xx||abs(a[i].s-yy)==abs(a[i].f-xx))
{
vis[j]++;
continue;
}
}
}
bool ans=false;
for(int x1:vis)
{
if(x1==n)
ans=true;
}
// cout<<endl;
if(ans)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
1002.Dragon slayer(BFS+剪枝)
题意:给你一个$n,m(1\leq n,m\leq 15)$表示有一个$0..n,0..m$的二维棋盘,给你$x_s,y_s,x_t,y_t$,表示人在$(x_s+0.5,y_s+0.5)$,龙在$(x_t+0.5,y_t+0.5)$。并且给你$k(1\leq k\leq 15)$表示有$k$堵强,坐标为$x_1,y_1,x_2,y_2 (0\leq x_1,x_2\leq n , 0\leq y_1,y_2 \leq m) $,人或许走不通,但是可以破坏一整堵墙,问破坏的最小次数。
思路:首先思考一下这个坐标$+0.5$代表的是什么意思,相当于是在棋盘正中间,但是我现在可以将其都往左下角移动,让他站在棋盘上,这样只需要到时候越界进行处理即可。
整体思路看到$k$最大为$15$,那么就想到状态压缩,枚举$2^{15}$个状态,每一位如果为$1$则表示需要拆除。加上一个剪枝,如果当前的$1$的个数大于我目前的ans那么就不进入BFS中。BFS就是遍历进行类似于染色的操作,观察是否可以到达龙的位置.
for (int state = 0; state < (1<<k); state++)
{
int cnt = 0, t = state;
while (t)
{
if (t&1) cnt++;
t>>=1;
}
if (cnt>=ans) continue;//剪枝
if (BFS(state))
ans = Min(ans,cnt);//取最小值
}
然后就是BFS的写法,BFS就是染色,一开始将所有的vis清空,然后将起点push到queue中,对四个方向进行判断是否越界,是否出现,然后再判断经过是否有墙壁阻挡。
判断墙壁阻挡这里有些麻烦,因为我之前都是向左下角移动的0.5,所以这里我分为两类:

因为都往左下平移0.5的缘故,所以判断墙的时候需要特殊处理一下:
- 如果是向上向右的话,则需要判断$(x+1,y+1)$位置与目标位置$(nx,ny)$进行比较;
- 如果是向左向下的话,则需要判断$(x,y)$位置与目标位置$(nx+1,ny+1)$进行比较。
判断是否有墙则需要枚举$k$个墙,如果状态的当前那一位如果是$1$则表示已经拆除,则continue,否则就进行判断。也有两种情况,一种是横着,一种是竖着,则需要满足四个端点的x或者y是相同的,并且墙的两端在这这两点的两端。
int yue(int p,int x1, int y1, int x2, int y2)
{
if (x1 > x2) swap(x1, x2);
if (y1 > y2) swap(y1, y2);
for (int i=1;i<=k;i++)//墙是1..k的顺序
{
if ((p>>i-1)&1) continue;//为什么减一,因为一开始向右移动0位
if ( x1==x2 && wall[i].x1==wall[i].x2 && x1==wall[i].x1 && wall[i].y1<=y1 && y2<=wall[i].y2)
return 1;
if ( y1==y2 && wall[i].y1==wall[i].y2 && y1==wall[i].y1 && wall[i].x1<=x1 && x2<=wall[i].x2)
return 1;
}
return 0;
}
那么BFS的代码就很简单了,主要就是判断是否进入队列那里处理,与其他无异,请见下。
代码:
struct node
{
int x1,x2,y1,y2;
}wall[20];
int sx,sy,tx,ty;
int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
inline bool check(int x,int y)
{
if (x<0||x>n-1||y<0||y>m-1) return 0;
return 1;
}
bool yue(int p,int x1, int y1, int x2, int y2)
{
if (x1 > x2) swap(x1, x2);
if (y1 > y2) swap(y1, y2);
for (int i=1;i<=k;i++)
{
if ((p>>i-1)&1) continue;
if ( x1==x2 && wall[i].x1==wall[i].x2 && x1==wall[i].x1 && wall[i].y1<=y1 && y2<=wall[i].y2)
return 1;
if ( y1==y2 && wall[i].y1==wall[i].y2 && y1==wall[i].y1 && wall[i].x1<=x1 && x2<=wall[i].x2)
return 1;
}
return 0;
}
inline bool BFS(int state)
{
for (int i=0;i<=n;i++)
for (int j=0;j<=m;j++)
vis[i][j] = 0;
queue<PII> q;
q.push(make_pair(sx,sy));
vis[sx][sy] = 1;
while (!q.empty())
{
PII u = q.front();q.pop();
int x = u.first, y = u.second;
for (int i=0;i<=3;i++)
{
int nx = x+dx[i], ny = y+dy[i];
if (check(nx,ny)==false) continue;
if (vis[nx][ny]) continue;
if ((i==1||i==2)&&yue(state,nx,ny,x+1,y+1)==0)
{
if (nx==tx&&ny==ty) {
return true;
}
vis[nx][ny] = 1;
q.push(make_pair(nx,ny));
}
if ((i==0||i==3)&&yue(state,nx+1,ny+1,x,y)==0)
{
if (nx==tx&&ny==ty) {
return true;
}
vis[nx][ny] = 1;
q.push(make_pair(nx,ny));
}
}
}
return false;
}
inline void Case_Test()
{
cin>>n>>m>>k;
ans = inf;
cin>>sx>>sy>>tx>>ty;
for (int i=1;i<=k;i++)
{
cin>>wall[i].x1>>wall[i].y1>>wall[i].x2>>wall[i].y2;
if (wall[i].x1>wall[i].x2) swap(wall[i].x1,wall[i].x2);
if (wall[i].y1>wall[i].y2) swap(wall[i].y1,wall[i].y2);
}
for (int state = 0; state < (1<<k); state++)
{
int cnt = 0, t = state;
while (t)
{
if (t&1) cnt++;
t>>=1;
}
if (cnt>=ans) continue;
if (BFS(state))
ans = Min(ans,cnt);
}
cout<<ans<<endl;
}

