总结
虽然前几次也在打,但是这次重新开始做总结,这场赛中只做出两个题,有点不舒服加上开摆E就没做了,最后补出E和G(F有点难),G有一个bitset优化技巧
比赛链接:Tasks - AtCoder Beginner Contest 258
A.When?
简单不表
这里有一个输出时间的技巧:(例如输出22:03)
h = 22, m = 3;
cout<<hh<<":"<<m/10<<m%10<<endl;
这样就不用if判断或者fill什么操作了
B.Number Box
不表
这里也有技巧,就是表示上下左右以及四个对角线的方向如何表示?
我是写了8个for循环,然后用两个if判断x,y是否越界,很蠢...看jly代码——
for (int dx = -1; dx <= 1; dx++) {
for (int dy = -1; dy <= 1; dy++) {
if (dx == 0 && dy == 0)
continue;
...
}
}
这样就能模拟出8个方向...也就是
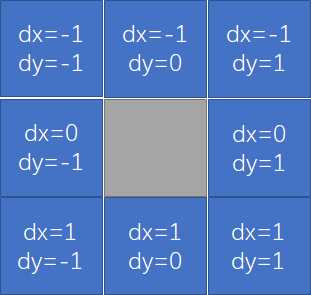
C.Rotation
每次O(1)输出,只需要累加x即可,然后取模
代码:
inline void Case_Test()
{
cin>>n>>m>>s;
s = " "+s;
while (m--)
{
cin>>op>>x;
if (op==1)
tag = (tag + x)%n;
else
{
if (x>tag)
cout<<s[x-tag]<<endl;
else
cout<<s[n-tag+x]<<endl;
}
}
}
D.Trophy(思维)
题意
给你$n$关游戏,你需要通过关卡$x$次(不论第几关,一共$x$关即可)。每关第一次需要花费$a_i$时间看视频,然后花$b_i$时间通过,后面就不用看视频了,每次只需要花费$b_i$即可通过。问通关$x$需要最少花费多少时间?
思路
每次扫一遍,扫到第$i$关维护需要都通关一次需要$res$时间,不难看出$res = \sum_{k=1}^i(a_k+b_k)$。然后一路上维护最小$b_i$值,也就是说我通关$i$个关卡,还需要$x-i$关,都用这个最小$b_i$通过,每次对答案$ans$取最小值即可
代码
inline void Case_Test()
{
cin>>n>>x;
ans = 9223372036854775807;
int pre = INF;
int res = 0;
for (int i=1;i<=n;i++)
{
cin>>a[i]>>b[i];
pre = Min(b[i],pre);
res += a[i]+b[i];
ans = Min(ans,res+(x-i)*pre);
}
cout<<ans;
}
E.Packing Potatoes(二分+思维+循环节)
题意
我有无限个土豆,有一个长度为$n$的重量为$w_i$序列无限循环着(在一个传送带上),还有一个值$x$。每次在传送带上将当前土豆放入当前盒子中,如果重量大于等于$x$,那么就封装起来,重新拿出一个新盒子继续装。将有若干次询问,每次询问第$k$个盒子里面有多少个土豆。
思路
不难想到这个肯定会有循环节,那么我们需要去找循环节,找循环节的时候需要注意一个问题,开头的可能不是循环节:
例如:盒子是8,3,4,4,2,5,6,7,4,4,2,5,6,7,4...
那么前面8,3就不是循环节,(8,3,[4,4,2,5,6,7],[4,4,2,5,6,7,4]...)
然后怎么思考呢,我有$a_1,a_2,...,a_n$序列代表土豆重量,因为是循环的,会取完最后一个然后再回头取第一个,所以我需要扩展成两倍变成:$a_1,a_2,...,a_n,a_1,a_2,...,a_n$这样我可以越界去取。
再用前缀和优化,这样可以在$O(1)$的时间复杂度求出$[l,r]$内的土豆总重量。
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=n+1;i<=2*n;i++) a[i] = a[i-n];
for (int i=1;i<=2*n;i++)
pre[i] = pre[i-1] + a[i];
int sum = pre[n];
然后就去寻找循环节,不难想到,当空盒子第一个面临$x$号土豆再次出现的时候,就是循环节出现的时候,因为会跟第一次出现的情况一模一样。
一开始设置一个指针t=1指向当前进来的那个土豆,然后进入循环。每次对于$x$进行整除取模处理,因为$x$可能很大,我上面扩展的$2sum都不够
int t = 1;
while (1)
{
int res = x % sum, g = x / sum;
...
}
这里判断一下,如果这时候res==0,就说明整除了,说明不用继续下去了,每次都是这个土豆开始,到它上一个土豆结束,然后又从这个土豆开始。
然后就是在整个a数组中判断大于$x$的时候是什么时候,这个时候因为是前缀和处理,所以lower_bound的时候需要判断的是res+pre[t-1],而不是res(可以想一下为什么)。
那么个数就是num = pos-t+1 + g*n,包括当前余数需要的和整除需要的。
并且设置当前的t标志数组vis[t]=1,如果下次还是t开始的话可以break退出了。
我这里设置了一下下标,当前第cnt个盒子对应哪个土豆开始的(t),这样到时候找不在循环节内的就好找了,t也赋值为下一次位置t = pos % n + 1
最后循环出来之后可以用b数组找到哪个开始结束不在循环节内,最后每次读入的时候判断一下,如果不用取模直接输出就好。
代码
写的很乱,不过思考都写在上面了。
inline void Case_Test()
{
cin>>n>>q>>x;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=n+1;i<=2*n;i++) a[i] = a[i-n];
for (int i=1;i<=2*n;i++)
pre[i] = pre[i-1] + a[i];
int sum = pre[n];
int t = 1;
while (1)
{
int res = x % sum, g = x / sum;
if (res == 0)
{
pack[++cnt] = g*n;
b[cnt] = t;
break;
}
int pos = lower_bound(pre+1,pre+1+2*n,res+pre[t-1])-pre;
int num = pos - t + 1;
vis[t] = 1;
pack[++cnt] = num + g*n;
b[cnt] = t;
t = pos % n + 1;
if (vis[t]) break;
}
for (int i=1;i<=cnt;i++)
if (b[i]==t) {t = i;break;}
t--;
int p = cnt - t;
while (q--)
{
cin>>k;
if (k<=cnt) cout<<pack[k]<<endl;
else cout<<pack[(k-t-1)%p+t+1]<<endl;
}
}
G-Triangle(bitset)
题意
给你一个$n\times n$的01矩阵,$a[i][j]=1$则表示在顶点$i$和顶点$j$之间有一条边。问你能否找到一个三元组$(i,j,k)$满足$1\leq i < j < k\leq n$满足$i$到$j$有一条边,$j$到$k$有一条边,$k$到$i$有一条边。
思路
先从暴力考虑,枚举$i,j$,且$a[i][j]=1$然后枚举$k$看有多少个$k$满足$a[i][k]=a[j][k]=1$。
发现这个东西就是集合$S_i$与$S_j$取交集之后的$1$的个数,也就是$|S_i \cap S_j|$,其中为了不重复,$S_i$表示满足$j>i,a[i][j]=1$的$j$集合,于是可以用bitset来优化。
代码
bitset<N> S[N];
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
cin>>c;
a[i][j] = c-'0';
if (j>i) S[i].set(j,c-'0');
}
for (int i=1;i<=n;i++)
for (int j=i+1;j<=n;j++)
if (a[i][j])
ans += (S[i]&S[j]).count();
cout<<ans;
}
