AcWing周赛41

写在前面

排名：26/2510
过题数：3/3 AK！

上周因为自己过21岁生日就没有打周赛40，我这一次又完成了AK的最低标准，并且！！这次来到了排名26，可惜的是这一次的A题wa了一发，耽误了时间也得到了罚时的滋味，不然我算了一下，大概能到17名左右，这也还能的到y总的赞美哈哈哈（念id），下次加油！也许这一次是有了npy的buff加成哈哈哈。

A.组合字符串（枚举+贪心）

题意

题目链接：AcWing 4308. 组合字符串 - AcWing

给定两个由小写字母构成的字符串 $s_1,s_2$。
现在，请你生成一个新字符串 $s_3$，要求 $s_3=s_1^\prime+s_2^\prime$ 且 $s_3$的字典序尽可能小。
$s_1^\prime$是指 $s_1$ 的非空前缀，$s_2^\prime$ 是指 $s_2$ 的非空前缀。
一个字符串的最长前缀即是它本身。

就是给你两个字符串，然后需要取出各部分的前缀子串来拼出一个字典序最少的，而且是有顺序的

思路

就类似于双指针，每个从开头枚举，因为要求字典序最小，那么就比较两个最高位开始，如果s1[i]>=s2[0]的话，那么就break，不然就一直是s1[i]较好
为什么只比较s2的第一位s2[0]呢，因为假如轮到了s2[0]，那么不需要再输出其他的了，这个时候字典序是最小的
记得最后一定要输出一个s2[0]，我wa就是循环里的≥写成了>，找了几十秒自信交上去了AC了。

代码

inline void Case_Test()
{
    cin>>s1>>s2;
    cout<<s1[0];
    for (int i=1;i<s1.length();i++)
    {
        if (s1[i]>=s2[0]) break;
        cout<<s1[i];
    }
    cout<<s2[0];
}

B.消灭老鼠（STL）

题意

题目链接：AcWing 4309. 消灭老鼠 - AcWing
在一个二维的图里面，给出原点和若干个点，求有多少不同的斜率

思路

最近也是做了一些这种斜率题目，还是拿PII存比较好，毕竟会有精度损失，经过测验，不需要判断负号，因为gcd会改正过来，但是好像编译器不一样就会出事？还是y总的比较全面

代码

set<PII> st;
PII k;
inline void Case_Test()
{
    cin>>n>>x0>>y_0;
    for (int i=1;i<=n;i++)
    {
        cin>>x>>y;
        x-=x0;y-=y_0;
        int t=gcd(x,y);
        //x/=t,y/=t,
        //if (x<0) x=-x,y=-y
        st.insert({x/t,y/t});
    }
    cout<<st.size();
}

C.树的DFS（DFS序/树形DP）

题意

题目链接：AcWing 4310. 树的DFS - AcWing
给出一个树，父节点一定小于子结点，然后dfs对树进行遍历，而遍历有一个顺序：

我们规定，当遍历（或回溯）到某一节点时，下一个遍历的目标应该是它的未经遍历的子节点中编号最小的那一个子节点。

举例子

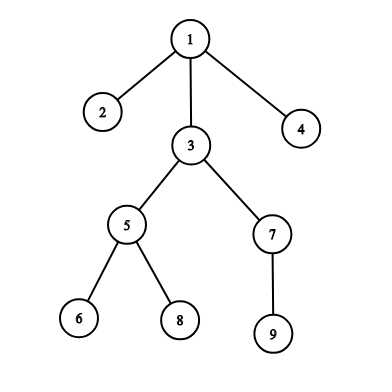
如果遍历根节点为 1 号节点的子树，则子树内各节点的遍历顺序为 [1,2,3,5,6,8,7,9,4]。
如果遍历根节点为 3 号节点的子树，则子树内各节点的遍历顺序为 [3,5,6,8,7,9]。
如果遍历根节点为 7 号节点的子树，则子树内各节点的遍历顺序为 [7,9]。
如果遍历根节点为 9 号节点的子树，则子树内各节点的遍历顺序为 [9]。

每次询问给出$u_i$和$k$，求在节点$u_i$开始下，第k次遍历的节点是多少，如果没有则输出-1，注意自己算第一次

比如给出5，2，那么能看到上面的图片，5这颗子树首先是5，然后是6，输出6，接下来是8，然后没有了

思路

其实一开始我是想放弃的，但是我想到了我的目标就是AK，最后也没想到能杀进前30哈哈哈，好吧接着说思路。
首先说一下暴力说法，暴力的话那就是对于每一次询问来一次dfs，这样肯定是不行的，那我们就能想到记忆化，对吧？
然后我就去想是否能够一次dfs完，毕竟看这个数据经验告诉我是的，然后发现我可以统计dfs序，就跟Tarjan里面的dfn一样，自己推了一遍发现确实是的。
那么问题可以转化为，你已知了：1,2,3,4,5,6,7...然后问你，3后面包括自己2位是什么？如果没有则输出-1，但是这里有点噢，就是说3后面的位数是有限的，最近做了不少树形dp，这点还是能处理的，dfs完毕往上更新即可

ps:这是能让我为数不多的用vector建图的，因为它要求从小到大的，用链式前向星的话应该是无法做到的吧

代码

vector<int> e[N];
inline void dfs(int x)
{
    dfn[++cnt]=x;//这里其实就是一个双向转换，跟hash一样互相指
    a[x]=cnt;
    num[x]=1;
    for (auto y:e[x])
    {
        dfs(y);
        num[x]+=num[y];
    }
}
inline void Case_Test()
{
    cin>>n>>q;
    for (int i=2;i<=n;i++)
    {
        cin>>x;
        e[x].push_back(i);
    }
    for (int i=1;i<=n;i++) sort(e[i].begin(),e[i].end());
    dfs(1);
    while (q--)
    {
        cin>>x>>k;
        m=a[x];
        int res=num[x];
        if (res>=k) cout<<dfn[ m+k-1 ]<<endl;
        else cout<<-1<<endl;
    }
}