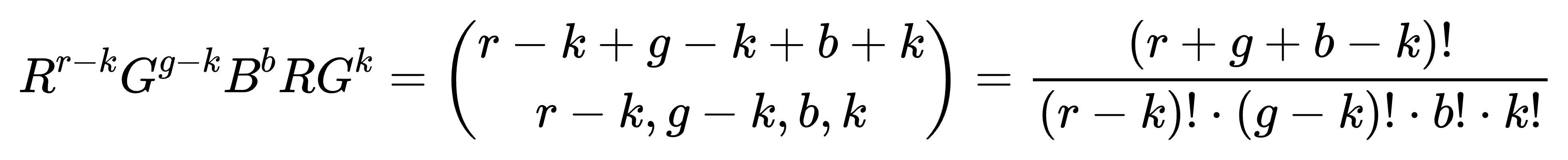这波史无前例abc做出六个题,G没有突破成功...是一个容斥...也可以是一个组合数学,我用组合数学做的,上大分!

比赛链接:ABC266
A.Middle Letter
输出奇数长度的中间字符串的字母
cout<<s[s.size()/2];即可
B.Modulo Number
给你一个$-10^{18}\leq x\leq 10^{18}$的数字,请对$998244353$取模,输出正数。
这个题考点就是负数,比如-5 % 2的结果是-1而不是1,所以我们先取模然后再加上mod再取模,这样就能解决负数问题,正数也没有影响。
inline void Case_Test()
{
cin>>n;
cout<<((n%mod)+mod)%mod;
}C.Convex Quadrilateral(判断凸多边形)
顺时针给你一个四边形的四个点的坐标,判断是否是凸多边形。
方法一:用计算几何的方法,叉积判断是正还是负,请见POJ2318 Toys(计算几何)- CarryNotKarry。
每次把相邻的两个点及其本身进行判断,判断下一个点是否在上一条线的一边,具体自己确定。
代码:
PII p[6];
int cross(PII a,PII b,PII c)
{
PII r1(c.fi-b.fi,c.se-b.se),r2(a.fi-b.fi,a.se-b.se);
int res = r1.fi*r2.se-r1.se*r2.fi;
return res;
}
inline void Case_Test()
{
for (int i=1;i<=4;i++)
cin>>p[i].fi>>p[i].se;
p[5] = p[1];
p[0] = p[4];
bool ok = true;
for (int i=1;i<=4;i++)
{
if (cross(p[i-1],p[i],p[i+1])<0)
ok = false;
}
if (ok) Yes;
else No;
}方法二:用面积计算,如果是凸多边形,将四边形切成两个三角形面积相加是相等的。
而如果不是,那么面积相加是不相等的。

上面两三角形面积相加相等,下面两三角形面积相加不相等
代码:
def solve():
xa, ya = MI()
xb, yb = MI()
xc, yc = MI()
xd, yd = MI()
def S(x1, y1, x2, y2, x3, y3):
a = ((x1 - x2) ** 2 + (y1 - y2) ** 2) **.5
b = ((x2 - x3) ** 2 + (y2 - y3) ** 2) **.5
c = ((x3 - x1) ** 2 + (y3 - y1) ** 2) **.5
p = (a + b + c) / 2
return (p * (p - a) * (p - b) * (p - c)) **.5
eps = 1e-8
if abs(S(xa, ya, xb, yb, xc, yc) + S(xc, yc, xd, yd, xa, ya) - S(xb, yb, xc, yc, xd, yd) - S(xd, yd, xa, ya, xb, yb)) < eps:
print('Yes')
else:
print('No')
D.Snuke Panic (1D)(DP)
题意:你现在在一维的线段上,有5个坐标分别是$0,1,2,3,4$,你现在在$0$位置上,你每秒可以向左向右走一步,然后你有若干次奖励,奖励在$T_i$时刻出现在$X_i$,奖励增加$A_i$,你最大可以获得的收益是多少。
思路:一开始还不会写,突然想到DP可以这么定义dp[i][j=0/1/2/3/4]表示第i时刻在第j处的最大奖励。
那么转移方程如何来?对于当前的dp[i][j]只能从上一个时间i-1的相邻转移j-1/j+1而来,如果是边界那么只有一种能转移。二者取max即可,如果当前有奖励那么当然加上。
代码:
int dp[N][5];
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
cin>>t[i]>>x[i]>>a[i];
for (int i=0;i<5;i++)
dp[0][i] = -INF;//一开始都设置为-INF
dp[0][0] = 0;//只有初始位置才是0可以开始转移
int cur = 1;
for (int i=1;i<=100000;i++)
{
for (int j=0;j<4;j++)
dp[i][j] = max({dp[i-1][j-1],dp[i-1][j+1],dp[i-1][j]});
dp[i][0] = Max(dp[i-1][0],dp[i-1][1]);
dp[i][4] = Max(dp[i-1][4],dp[i-1][3]);
if (t[cur]==i)//如果当前时间有奖励
{
dp[i][x[cur]] += a[cur];//那么这个时候就加上
cur++;//判断的奖励往下移动一个
}
for (int j=0;j<=4;j++)
ans = Max(ans, dp[i][j]);//途中都判断一下
}
cout<<ans;
}E.Throwing the Die(期望DP)
题意:你有一个六面骰子,你将进行$n$次试验:
- 如果现在是第$n$轮,你骰到了$x$,那么积分是$x$
- 如果在途中可以选择结束,骰到了$x$那么积分就是$x$不再继续。
问$n$轮过后的期望是多少。
思路:
当$n=1$的时候,答案是$3.500000$,不难想,选到什么就是什么。
那么多的时候呢?答案就变了,假如当前是$5$,我骰到$2$肯定是不好的,所以我选择到$5$就结束。
我们当然希望选到$6$就直接结束。
定义$f[i]$为第$i$轮的期望,那么$f[1]=3.500000$,然后开始枚举$n$次递推:
并且枚举骰出的$j=1,2,3,4,5,6$
- 如果当前$j<f[i-1]$这么说明我当前这一次比上次期望还低,那么就有$\frac{1}{6}$的概率选到这个,代表没有贡献,不如不骰这次。
f[i]+=f[i-1]/6.0 - 否则,那么我肯定选择骰这一次,并且概率直接替换这次的。
f[i]+=j/6.0
代码:
double f[110];
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=6;i++)
f[1] += 1.0/6.0*(double)i;
for (int i=2;i<=n;i++)
{
for (int j=1;j<=6;j++)
if (j<f[i-1])
f[i] += f[i-1]/6.0;
else
f[i] += j/6.0;
}
cout<<fixed<<setprecision(10)<<f[n];
}F.Well-defined Path Queries on a Namori(基环树)
题意:给你一个$n$点$n$边的图,有若干次询问,问点u到点v是否是一条简单路径(也就是是否只有一条路到达)
思路:这个题就是基环树,可以见AcWing1738.蹄球(基环树|思维) - CarryNotKarry。
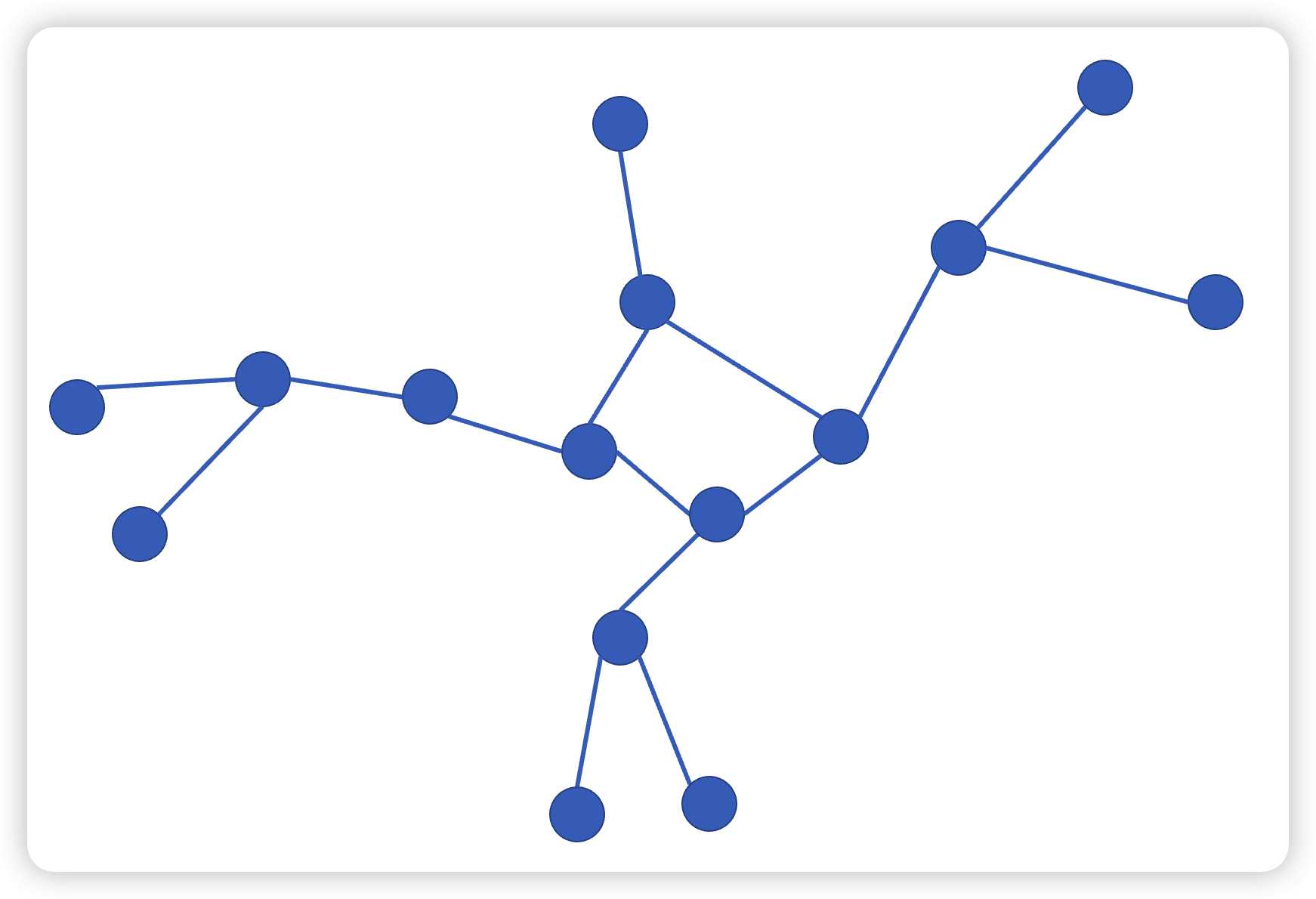
n点n边的基环树,也就是中间是个换,环上都一个子树(包括自己)
我们不难想到,只要经过这个环,那么就是一定不是简单路径,环上的两个点也是一样的。
那么我们可以用到基环树最基本的一个操作,对环上的点对其子树染色:
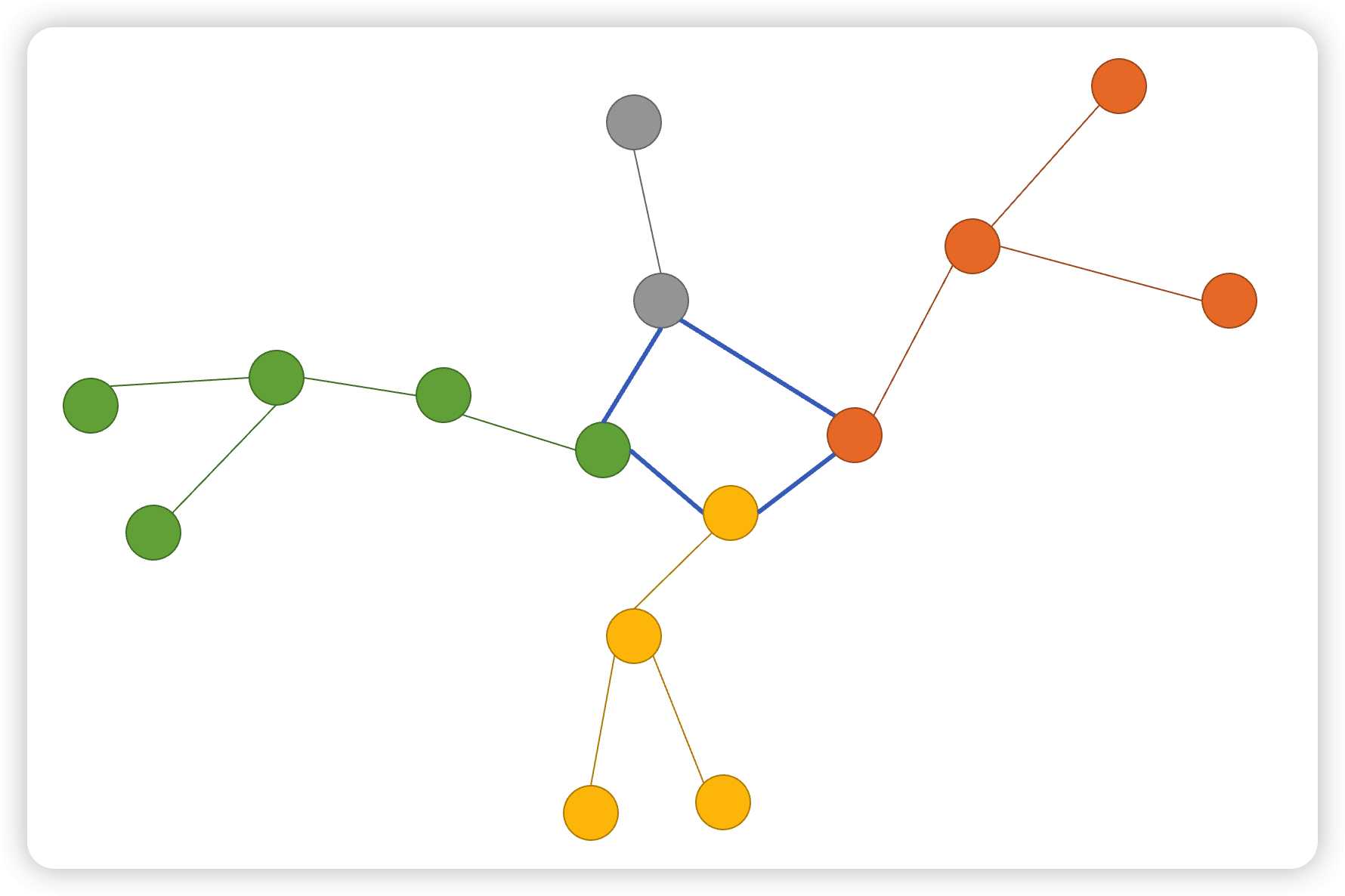
对子树染色
其实很简单,从点开始并且只需要判断不要染到环上的即可。
那么如何判断环?直接拓扑排序即可。
最后可以把问题转化为是否是同样一个颜色即可。
代码:
inline void dfs(int x)
{
col[x] = col_num;
for (int i=head[x];i;i=edge[i].next)
{
int y = edge[i].to;
if (vis[y]||col[y]) continue;
dfs(y);
}
}
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
in[u]++;in[v]++;
}
queue<int> q;
for (int i=1;i<=n;i++)
{
vis[i] = 1;
if (in[i]==1) q.push(i);
}
while (!q.empty())
{
int x = q.front();q.pop();
vis[x] = false;
for (int i=head[x];i;i=edge[i].next)
{
int y = edge[i].to;
if (vis[y]==false) continue;
in[y]--;
if (in[y]==1) q.push(y);
}
}
for (int i=1;i<=n;i++)
{
if (!vis[i]) continue;
++col_num;
dfs(i);
}
cin>>p;
while (p--)
{
cin>>x>>y;
if (col[x]==col[y]) Yes;
else No;
}
}G.Yet Another RGB Sequence(组合数学)
题意:你有$r$个R,$g$个G,$b$个B,你需要对其进行排列,并且有且仅有$k$个RG。例如r=2,g=2,b=1,k=1中符合条件的有RGRBG,但是RGRGB就不可以,因为RG出现了两次
思路:我一开始想那肯定先从中选出$k$个R和G,这样变成了有$r-k$个R,$g-k$个G,$b$个B,$k$个RG。那么就是:
这样就是固定RG,其他任意排列,但是其他任意排列也会导致会产生新的RG,所以需要用到容斥——官方题解
但是可以换种方法思考:
我们先不管G,先管$r-k$个R,$b$个B,$k$个RG(先不管$g-k$个G)。这样排列则有:
$$
R^{r-k}B^bRG^k=\frac{(r-k+b+k)!}{(r-k)!\cdot b!\cdot k!}
$$
那么这里面一共有$r-k+b+k=r+b$个元素,其中有$r-k$个R,我要放剩下的G则不能放在R后面,所以现在问题变成了
给你$r+b-(r-k)=b+k$个
o,你需要插入$g-k$个*,问有多少种方案。
_o_o_o_o_o_其中要插入若干的*,_是空隙,且一个空隙能插入多个*。比如ooo**oo***oo
再简单化一下:你有$a$个o,需要插入$b$个*有多少种方案。
其实就是$a+b$个位置,选出$b$个给MARKDOWN_HASH3389dae361af79b04c9c8e7057f60cc6MARKDOWNHASH,所以答案是$\binom{a+b}{b} $,也就是$C{a+b}^b$。
所以上面插入$g-k$个MARKDOWN_HASHdfcf28d0734569a6a693bc8194de62bfMARKDOWNHASH答案就是$\binom{b+k+g-k}{g-k}=C{g-k}^{b+g}$
那么答案就是二者相乘
$$
ans = \frac{(r-k+b+k)!}{(r-k)!\cdot b!\cdot k!} \times C_{g-k}^{b+g}
$$
代码:
int ksm(int a,int b,int p=mod,int res=1)
{
for( ; b ; a=a*a%p, b>>=1) if(b&1) res=res*a%p;
return res;
}
int fac[N],inv[N];
void init(int n=N-2)
{
inv[0]=fac[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
inv[n]=ksm(fac[n],mod-2);
for(int i=n-1;i>=1;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
int C(int n,int m)
{
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
inline void Case_Test()
{
cin>>r>>g>>b>>k;
ans = fac[r+b]*inv[r-k]%mod*inv[b]%mod*inv[k]%mod*C(b+g,g-k)%mod;
cout<<ans;
}