2022牛客多校·第六场（B树上差分,A构造）

这一场打得还算可以,团队合力共A五题，凭借罚时优势排列在前面。

J.Number Game（签到）

题意：给你三个数$a,b,c$以及$x$，你可以对下列两个操作进行任意次操作，请问最后是否能够达到$c=x$。
- 1) $B = A - B$
- 2) $C = B-C$

思路：自己模拟几遍发现其实就只有几种情况，比如$b$只有$a-b,b$两种，但是$c$能够造出很多种，为什么呢？我可以对于$b$的两种形态对$c$进行第二个操作。例如：
$$
c\Rightarrow (a-b)-c \Rightarrow b-(a-b)+c \Rightarrow (a-b)-b+(a-b)-c \Rightarrow \cdots
$$

就这么几种情况，最后找到规律就if即可。

代码：

#define No cout<<"No"<<endl
#define Yes {cout<<"Yes"<<endl;return;}
inline void Case_Test()
{
    cin>>a>>b>>c>>x;
    if (c==x||b-c==x) Yes;
    if ((a-2*b!=0)&&((x-c)%(a-2*b)==0||(x+c-b)%(a-2*b)==0)) Yes;
    if ((2*b-a!=0)&&((x+c-b)%(2*b-a)==0||(x-c)%(2*b-a)==0)) Yes;
    No;
}

B.Eezie and Pie（树上差分）

题意：给你一颗$n$边根为$1$的树，每个点都有一个权值$a_i$，可以往跟派送$a_i$次，求每个点最多能被访问多少次。

思路：这个题一眼树上差分，具体操作请看这篇文章（填坑）。
然后需要从下往上扫，就像bfs/拓扑排序一样，当下面的点扫完之后才轮到它，进行类似前缀和的操作即可。

代码：

void Build(int x,int pre)
{
    dep[x]=dep[pre]+1;
    f[x][0]=pre;
    for (int i=1;i<=20;i++)
        f[x][i]=f[ f[x][i-1] ][i-1];
    for (int i=head[x];i;i=edge[i].next)
        if (edge[i].to!=pre)
            Build(edge[i].to,x);
}
inline int find(int x)
{
    int p = a[x];
    for (int i=20;i>=0;i--)
        if ((p>>i)&1) x = f[x][i];
    return Max(x,1);
}//二进制拆位找祖先
inline void Case_Test()
{
    for (int i=2;i<N-2;i++) lg2[i] = lg2[i>>1]+1;
    n = read();
    for (int i=1;i<n;i++)
    {
        int u,v;
        u =read(); v = read();
        add(u,v);add(v,u);
        in[u]++;in[v]++;
    }
    Build(1,0);
    for (int i=1;i<=n;i++)
        a[i] = read();
    for (int i=1;i<=n;i++)
    {
        int o = find(i);//找祖先
        ans[i]++;
        ans[f[o][0]]--;
    }
    queue<int> q;
    for (int i=1;i<=n;i++)
        if (in[i]==1) q.push(i);
    while (!q.empty())
    {
        int x = q.front();q.pop();
        ans[f[x][0]] += ans[x];
        in[f[x][0]]--;
        if (in[f[x][0]]==1) q.push(f[x][0]);
    }
    for (int i=1;i<=n;i++) cout<<ans[i]<<" ";
}

G.Icon Design（签到）

题意：输出logo...

M.Z-Game on grid（思维）

题意：给你一个$n\times m$的棋盘，由A,B,.构成，一开始棋子$(1,1)$在左上角，Alice（先）和Bob（后）进行操作。每次可以选择$(x,y)\to (x+1,y)$或者$(x,y)\to (x,y+1)$，如果当前的点是A则Alice赢，B则Bob赢，最后大家都无棋可走（到达$(n,m)$）则游戏平局。

请问Alice是否能找到一条路一定使得自己Win,Lose,Draw？他并不知道Bob如何想的。

思路：这个题的坑点主要是：如果Alice想赢，那么Bob思考的是不想让Alice赢；如果Alice想平，那么Bob思考的是不想让Alice平；如果Alice想输，那么Bob思考的是不想让Alice输。

这跟平时的博弈不同，题目问的是能否找到一条路使得一定能够，所以如果有必输的方案，那么Bob可以选择让你赢。

所以我们想到一个染色方法，这里举想赢的例子。对于当前点$(x,y)$只有$(x+1,y),(x,y+1)$能够影响到它，那么我们就从下往上，从右往左开始扫，这样保证每一个点的时候他的右边和下面都是有的。

那么如何染呢？如果当前点的两边都同为A或者B，那么该点也是这个，如何理解呢，例如两边都是A，那么到达该点之后无论是Alice动还是Bob动都是Alice赢，这个点的A的意义是这样的。

那么如果不同怎么办，两边分别各有一个？那么就需要看曼哈顿距离的奇偶。看哪个能影响的。

最后看$(1,1)$被哪个颜色染了。

那么想输的时候怎么办呢？则需要全局的A,B对调一下即可，这时候就不想让你输。
平局的时候呢？都看成一个字母就行了，因为Alice这些都不想碰到。

代码：

inline void Case_Test()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
        {
            cin>>c[i][j];
            ch[i][j] = c[i][j];
        }
    c[n+1][m] = '.';
    c[n][m+1] = '.';
    for (int i=n;i>=1;i--)
    {
        for (int j=m;j>=1;j--)
        {
            if (c[i][j]!='.') continue;
            int d = i+j-2;
            if (i==n)
                c[i][j] = c[i][j+1];
            else if (j==m)
                c[i][j] = c[i+1][j];
            else
            {
                if (c[i+1][j]=='A'&&c[i][j+1]=='A')
                    c[i][j] = 'A';
                else if (c[i+1][j]=='B'&&c[i][j+1]=='B')
                    c[i][j] = 'B';
                else 
                {
                    if ((c[i+1][j]=='A'||c[i][j+1]=='A')&&d%2==0)
                        c[i][j] = 'A';
                    if ((c[i+1][j]=='B'||c[i][j+1]=='B')&&d%2==1)
                        c[i][j] = 'B';
                }
            }
        }
    }
    if (c[1][1]=='A') cout<<"yes ";
    else cout<<"no ";

    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            if (ch[i][j]=='.') c[i][j] = '.';
            else c[i][j] = 'B';

    for (int i=n;i>=1;i--)
    {
        for (int j=m;j>=1;j--)
        {
            if (c[i][j]!='.') continue;
            int d = i+j-2;
            if (i==n)
                c[i][j] = c[i][j+1];
            else if (j==m)
                c[i][j] = c[i+1][j];
            else
            {
                if (c[i+1][j]=='A'&&c[i][j+1]=='A')
                    c[i][j] = 'A';
                else if (c[i+1][j]=='B'&&c[i][j+1]=='B')
                    c[i][j] = 'B';
                else 
                {
                    if ((c[i+1][j]=='A'||c[i][j+1]=='A')&&d%2==0)
                        c[i][j] = 'A';
                    if ((c[i+1][j]=='B'||c[i][j+1]=='B')&&d%2==1)
                        c[i][j] = 'B';
                }
            }
        }
    }
    if (c[1][1]=='.') cout<<"yes ";
    else cout<<"no ";

    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            if (ch[i][j]=='.') c[i][j] = '.';
            else if (ch[i][j]=='A') c[i][j] = 'B';
            else c[i][j] = 'A';

    for (int i=n;i>=1;i--)
    {
        for (int j=m;j>=1;j--)
        {
            if (c[i][j]!='.') continue;
            int d = i+j-2;
            if (i==n)
                c[i][j] = c[i][j+1];
            else if (j==m)
                c[i][j] = c[i+1][j];
            else
            {
                if (c[i+1][j]=='A'&&c[i][j+1]=='A')
                    c[i][j] = 'A';
                else if (c[i+1][j]=='B'&&c[i][j+1]=='B')
                    c[i][j] = 'B';
                else 
                {
                    if ((c[i+1][j]=='A'||c[i][j+1]=='A')&&d%2==0)
                        c[i][j] = 'A';
                    if ((c[i+1][j]=='B'||c[i][j+1]=='B')&&d%2==1)
                        c[i][j] = 'B';
                }
            }
        }
    }
    if (c[1][1]=='A') cout<<"yes\n";
    else cout<<"no\n";
}

A.Array（构造）

题意：这是一个有趣的构造题.
给你一个长度为$n(n\leq 10^5)$的数组$a$，满足$\Sigma _{i=1}^{n}\frac{1}{a[i]} \leq \frac{1}{2}$。需要构造出一个$b$数组，必须满足在$ b$ 的每个连续的$ a[i] $个数中存在一个等于$i$的数

思路：

先来看例如$a[1]=3$的时候

a[1] = 3的时候

构造的方式是我们找到一个最大的$x$满足，$2^x\leq a_i$，也就是不大于$a_i$的最大的二的幂。例如$7\to 4,\ 8\to 8,\ 9\to 8$。那么我们按照这个构造，例如$a[1]=3$，那么我就是变成$a[1]=2$使得其每两个则放置一个$1$。这样构造的倒数之和小于$1$。

寻找最大的这个$x$可以通过内置函数一行写出，即1 << 31 - __builtin_clz(a[i])。

然后我们得到新的$a_i$进行从小到大的排序之后,暴力放置即可。

例如现在得到的是$a[]=\lbrace 4,8,8,8,8\rbrace $。我们按顺序依次放置，如果当前有了则往下放即可，例如$5$，每次加上自己的$a[i]$即可。最后随便填写即可。

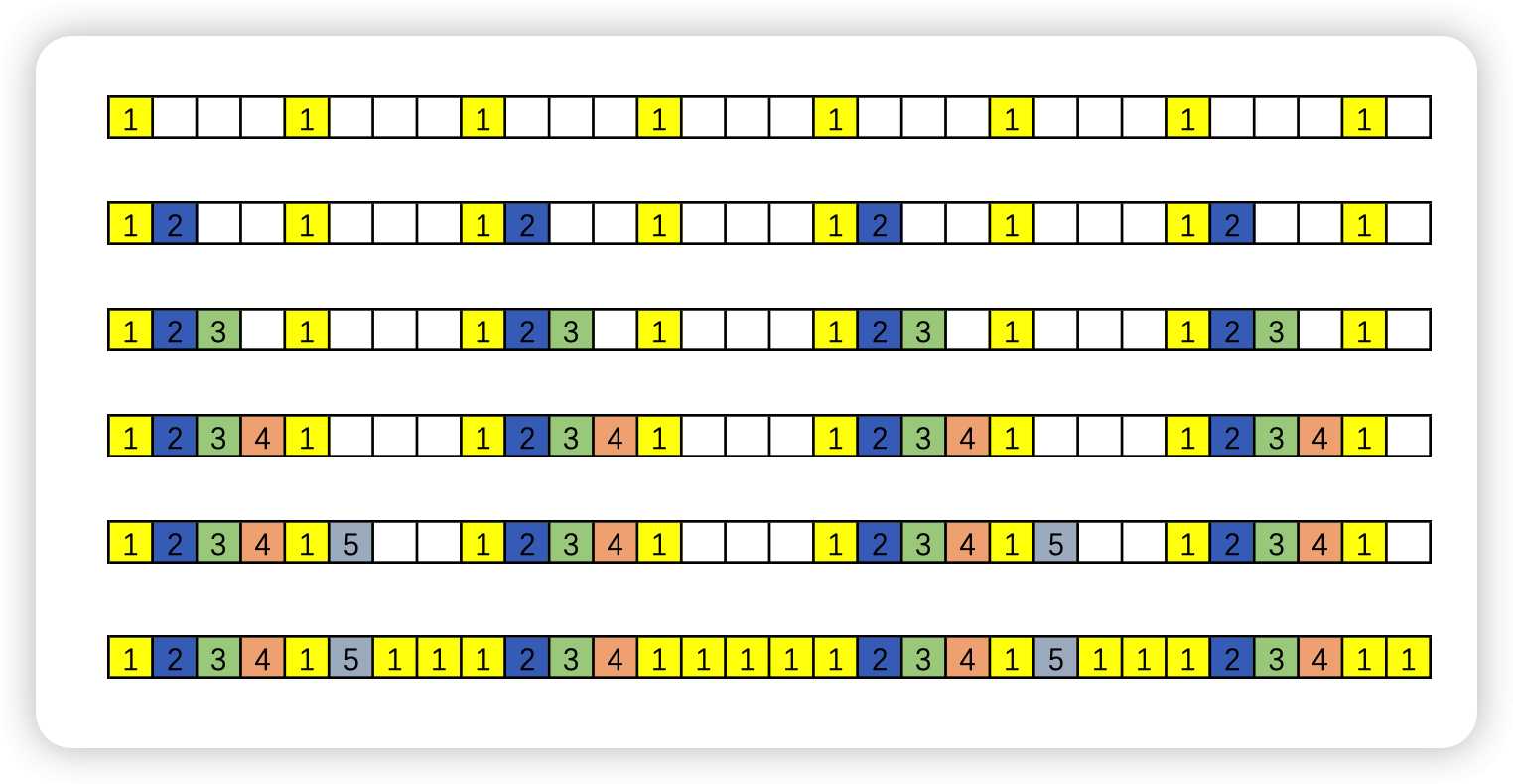
依次放置4,8,8,8,8

代码：

PII p[N];
inline void Case_Test()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>a[i];
        p[i] = make_pair(1ll<<31 - __builtin_clz(a[i]),i);
    }
    sort(p+1,p+1+n);
    int t = 1, maxn = 1<<18;
    for (int i=1;i<=n;i++)
    {
        while (ans[t]) t++;//往下枚举，不回头所以O(n)
        for (int j = t;j<=maxn;j+=p[i].first) ans[j] = p[i].second;//每次加上新的a[i]
    }
    cout<<maxn<<endl;
    for (int i=1;i<=maxn;i++) cout<<Max(1,ans[i])<<" ";//0就填1
}