现在是北京时间2022/7/27-21:20,距离比赛打完已经过去了2天,已经积累了牛客3还有杭电3没有写...明天又要打杭电4...这里就好像一个队列,当当前
size==2就在push前pop队首一样。
比赛链接:"蔚来杯"2022牛客暑期多校训练营3
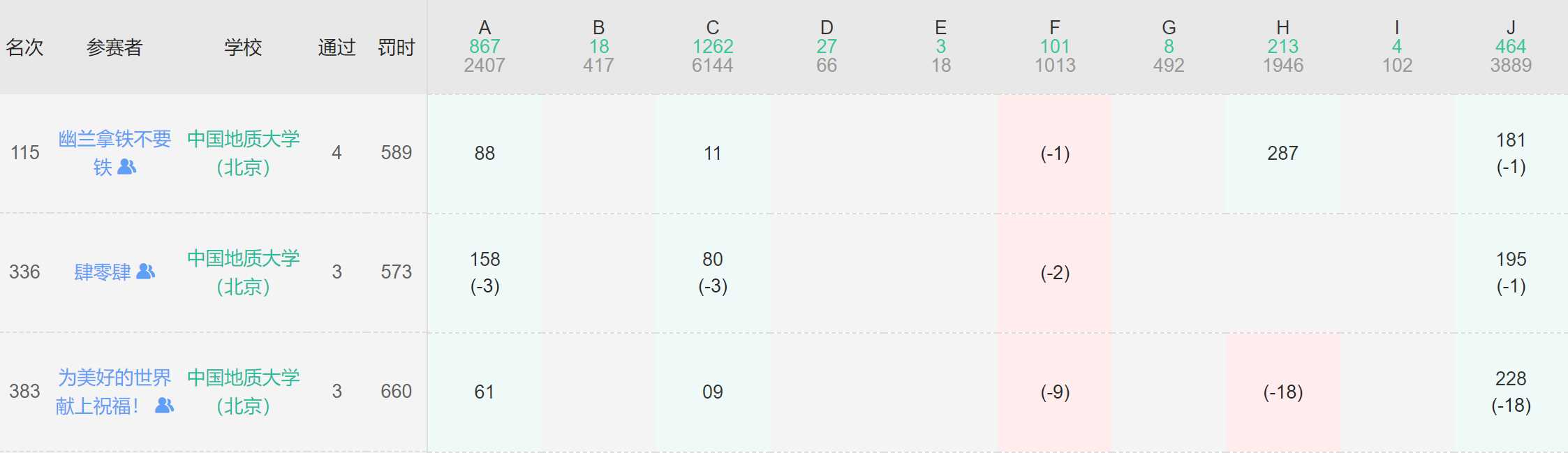
这一次在封榜后怒学一手后缀自动机(SAM),然后套了自己线段树的板子怒交一发H竟然过了,解绑后来到了史无前例的rk115。
C.Concatenation(排序)
题意:给你$n(1\leq n\leq 2e6)$的字符串,总字符串长度不超过$2e7$,求将其拼接的字典序最小的字符串。PS:出题人最后面说如果你用的算法是$O(nlogn)$,Good luck。
例如00,12,121三者应该是0012112,如果是0012121会发现比之前的要大。
思路:聪明的人一开始可能会看就是对这些排个序,然后输出,其实样例都过不去,这个题我是在OI时候做过原题,因为比较的是二者每次选最优的,其实比较a+b<b+a即可,但是这时间复杂度我一直不敢交...
听说$O(nlogn)$卡的很死,比如引用符号&没有加,则需要多两次的拷贝构造,这样常数很大过不去..
代码:
sort(s+1,s+n+1,[](const string& a,const string& b){
return a+b<b+a;
});
A.Ancestor(LCA,DFS序)
题意:给你都有$n(1\leq n\leq 10^5)$个结点的树$A$和树$B$并且两棵树每个点都有一个权值$a_i,b_i$,给你$k$个数字$x_1,x_2,...,x_k(x_i\in A,B)$,你需要删除一个点,求其他的点的在$A$树的剩下点$lca$的权值$a_{lca}$严格大于在$B$树剩下点的$b_{lca}$的删除的方案数。
思路:在这篇文章DFS序 - CarryNotKarry详细讲述了什么是DFS序,以及什么用法。这个题用到了结论就是:若干个点的$LCA$也就是DFS序最大的以及最小的两个结点的$LCA$。
所以这个题对于每一棵树不必要每次都对每个点都进行logn的$LCA$,只需要预处理出来DFS序,然后对于删除的情况分类,也就是将这$k$个点按照DFS序从小到大变成新的$x_1,x_2,...,x_k$,那么分为三种情况:
- 删除$x_1$,那么$anc=lca(x_2,x_k)$;
- 删除$x_{2...k-1}$,那么$anc=lca(x_1,x_k)$;
- 删除$x_k$,那么$anc=lca(x_1,x_{k-1})$.
所以对两个树都这样预处理之后,只需要判断删除的点是哪个即可.
我觉得这个题不应该现场过867个队伍...至少考察的挺多..
代码:
struct node
{
int to,next;
}edge1[N<<1],edge2[N<<1];
int head1[N],head2[N],cnt1,cnt2,dfn1[N],dfn2[N],dep1[N],dep2[N];
int lg2[N],f[N][21],g[N][21];
int cnte1,cnte2;
int typeA[N],typeB[N],resA,resB;
inline void add1(int x,int to)
{
edge1[++cnte1].to = to;
edge1[cnte1].next = head1[x];
head1[x] = cnte1;
}
inline void add2(int x,int to)
{
edge2[++cnte2].to = to;
edge2[cnte2].next = head2[x];
head2[x] = cnte2;
}
void build1(int x,int pre)
{
dep1[x]=dep1[pre]+1;
dfn1[x] = ++cnt1;
f[x][0]=pre;
for (int i=1;i<=20;i++)
f[x][i]=f[ f[x][i-1] ][i-1];
for (int i=head1[x];i;i=edge1[i].next)
if (edge1[i].to!=pre)
build1(edge1[i].to,x);
}
int lca1(int x,int y)
{
if (dep1[x]<dep1[y]) swap(x,y);
while (dep1[x]>dep1[y])
x=f[x][lg2[dep1[x]-dep1[y]]];
if (x==y) return x;
for (int i=lg2[dep1[x]];i>=0;i--)
if (f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
void build2(int x,int pre)
{
dep2[x]=dep2[pre]+1;
dfn2[x] = ++cnt2;
g[x][0]=pre;
for (int i=1;i<=20;i++)
g[x][i]=g[ g[x][i-1] ][i-1];
for (int i=head2[x];i;i=edge2[i].next)
if (edge2[i].to!=pre)
build2(edge2[i].to,x);
}
int lca2(int x,int y)
{
if (dep2[x]<dep2[y]) swap(x,y);
while (dep2[x]>dep2[y])
x=g[x][lg2[dep2[x]-dep2[y]]];
if (x==y) return x;
for (int i=lg2[dep2[x]];i>=0;i--)
if (g[x][i]!=g[y][i])
x=g[x][i],y=g[y][i];
return g[x][0];
}
struct node1
{
int x,id;
node1(){}
node1 (int _x,int _id):x(_x),id(_id){}
}aa[N],bb[N];
inline bool cmp(node1 &a,node1 b)
{
return a.x<b.x;
}
inline void Case_Test()
{
cin>>n>>k;
for (int i=2;i<=N-2;i++)
lg2[i]=lg2[i>>1]+1;
for (int i=1;i<=k;i++)
cin>>ky[i];
for (int i=1;i<=n;i++)
cin>>a[i];
for (int i=2;i<=n;i++)
{
cin>>x;
add1(x,i);
}
for (int i=1;i<=n;i++)
cin>>b[i];
for (int i=2;i<=n;i++)
{
cin>>x;
add2(x,i);
}
build1(1,0);
build2(1,0);
for (int i=1;i<=k;i++)
{
x = ky[i];
aa[i] = {dfn1[x],x};
bb[i] = {dfn2[x],x};
}
sort(aa+1,aa+k+1,cmp);
sort(bb+1,bb+k+1,cmp);
//----------A:1,k----------
resA = a[ lca1(aa[1].id,aa[k].id) ];//A :1~k
int res1,res2,res3;//B: (1->1~k),(2->2~k),(3->1~k-1)
res1 = b[ lca2(bb[1].id,bb[k].id) ];
res2 = b[ lca2(bb[2].id,bb[k].id) ];
res3 = b[ lca2(bb[1].id,bb[k-1].id) ];
ans = 0;
for (int i=1;i<=k;i++)//B
{
x = bb[i].id;
if (dfn1[x]==aa[1].x || dfn1[x]==aa[k].x) continue;
if (i==1) ans += (resA>res2);
else if (i==k) ans += (resA>res3);
else ans += (resA>res1);
}
//----------A:删1------------
resA = a[ lca1(aa[2].id,aa[k].id) ];//A :2~k
x = aa[1].id;
if (dfn2[x]==bb[1].x) ans += (resA>res2);
else if (dfn2[x]==bb[k].x) ans += (resA>res3);
else ans += (resA>res1);
//----------A:删k------------
resA = a[ lca1(aa[1].id,aa[k-1].id) ];//A :1~k-1
x = aa[k].id;
if (dfn2[x]==bb[1].x) ans += (resA>res2);
else if (dfn2[x]==bb[k].x) ans += (resA>res3);
else ans += (resA>res1);
cout<<ans;
}
J-Journey(01BFS)
题意:给你$n(1\leq n\leq 500000)$的十字路口,每个路口有$4$个方向,右转是不需要耗费时间的,其他需要耗费一点时间。然后给你一开始的起始位置和终止位置,求最小的时间。
思路:这个题主要是题目难读懂,在牛客反应也米有用,都想开喷了...实际上给你的$4$个方向下一个是上一个的右转,例如i=1时候0,0,3,4表示如果你现在在(3,1)的位置(这个表示在3号十字路口往1号式子路口那条有向线段上),你往右拐变成了(1,4)是不需要花费的,从(3,1)变成了(1,4)其实就是拐了个湾。理解了这个之后就好多了。
那么现在来看进行BFS,一共只有两种权值,一种是右转花费0,一种是其他选项(左转,直走,掉头)花费1。可以用Dijkstra最短路来做。
但是我这里用更快的01BFS:将权值$0$的放在双端队列(deque)前面,权值$1$的放在deque的后面。这样保证取出来每次都是当前最佳,权值最小的情况,如果当前队列首部就是终点可以直接输出退出。这里有一个01BFS的题目曾经写过:【双端队列广搜/搜索+图论】AcWing 2019.拖拉机 USACO 2012 March Contest Silver Division - CarryNotKarry。
然后不难,看代码吧,注意有一点不然会WA,就是判断的时候用map来判断是否入只队列一次,而应该是判断是否出队操作一次。因为先入队列的可能是放在后面的,不是最佳,后面进入的反而是最佳的,但是我取出来的时候是只取队列前面最佳,那么先进入放队列后面的则出栈就不操作了。
在Dijkstra中也是如此,我们用的标志数组不是判断它是否进队列一次,而是只对每个点松弛一次。
代码:
int c[N][5];
struct node
{
int x,y,sep;
};
map<PII,bool> mp;
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
for (int j=1;j<=4;j++)
cin>>c[i][j];
}
int sx,sy,tx,ty;
cin>>sx>>sy>>tx>>ty;
deque<node> q;
q.push_back({sx,sy,0});
//mp[make_pair(sx,sy)] = true;
while (!q.empty())
{
node t = q.front(); q.pop_front();
int to = t.y, fr = t.x, sep = t.sep;
if (mp[make_pair(fr,to)]) continue;
mp[make_pair(fr,to)] = true;//这样判断每个状态只进行一次操作是正确的
if (fr==tx&&to==ty) {cout<<sep;return;}
for (int i=1;i<=4;i++)
{
if (c[to][i]==0) continue;
//if (mp[make_pair(to,c[to][i])]) continue;
//mp[make_pair(to,c[to][i])] = true; 这样判断是否入队列一次就是会错
if (c[to][(i+2)%4+1]==fr)
q.push_front({to,c[to][i],sep});
else
q.push_back({to,c[to][i],sep+1});
}
}
cout<<-1;
}
H.Hacker(SAM+线段树)
题意:给你$n,m,k$表示有一个长度为$n$的原串$s$,以及有$k$个长度为$m$的字符串$b$进行询问,你将有一个长度为$m$的权值$v_i$,对于每次询问原串$s$与询问串$b$的匹配的若干个公共子串的最大子段和是多少。
例如s=carry和b=pparrpp进行判断,发现b中间的arr是第三个到第五个与s有公共子串,所以就比较$v_3+v_4+v_5$与答案进行更新,当然,b的ar也是符合条件的,所以也需要拿$v_3+v_4$进行比较。
思路:现学后缀自动机(SAM),这里的SAM能做到以第i个位置为后缀,前面有多少个字符串能与原串匹配。例如s=carrynotkarry,b=carrypk则是以下情况:
i=0 -> 1
i=1 -> 2
i=2 -> 3
i=3 -> 4
i=4 -> 5
i=5 -> 0
i=6 -> 1
然后我用线段树维护区间最大子段和,这个有点难,不过我之前在AcWing写过该题,直接CV过来:AcWing245 线段树-单点修改+区间求最大连续子段和 - CarryNotKarry。
那我需要对于每次都进行查询吗?不,只需要对每次最长的公共子串匹配即可,也就是对于上方的5和最后的1的时候,因为如果是[2,4]是最大子段和的话,我查询[1,5]的时候也能查询出来,而不是每次匹配就进行logn的线段树查询。
代码:
- SAM部分
struct Suffix_Automata
{
int len[N << 1];
int lnk[N << 1];
int cnt[N << 1];
int sub[N << 1];
int nxt[N << 1][26];
int idx;
int last;
void init()
{
last = idx = 1;
lnk[1] = len[1] = 0;
}
void clear()
{
memset(len, 0, sizeof len);
memset(lnk, 0, sizeof lnk);
memset(cnt, 0, sizeof cnt);
memset(nxt, 0, sizeof nxt);
}
void extend(int c)
{
int x = ++idx;
len[x] = len[last] + 1;
sub[x] = 1;
int p;
for (p = last; p && !nxt[p][c]; p = lnk[p])
nxt[p][c] = x;
if (!p)
lnk[x] = 1, cnt[1]++;
else
{
int q = nxt[p][c];
if (len[p] + 1 == len[q])
lnk[x] = q, cnt[q]++;
else
{
int nq = ++idx;
len[nq] = len[p] + 1;
lnk[nq] = lnk[q];
memcpy(nxt[nq], nxt[q], sizeof nxt[q]);
for (; p && nxt[p][c] == q; p = lnk[p])
nxt[p][c] = nq;
lnk[q] = lnk[x] = nq;
cnt[nq] += 2;
}
}
last = x;
}
}sam;
void solve()
{
int len2 = strlen(b);
int u = 1, L = 0, pre;
for (int i = 0; i < len2; i++)
{
int id = b[i] - 'a';
while (!sam.nxt[u][id] && u != 1)
u = sam.lnk[u], L = sam.len[u];
if (sam.nxt[u][id] != 0)
u = sam.nxt[u][id], ++L;
pre = L;
if (L!=pre+1)
ans = Max(ans, query(1,i-L+1+1,i+1).tmax);
}
if (L) ans = Max(ans, query(1,len2-1-L+1+1,len2).tmax);
cout << ans << endl;
}
- 线段树部分
#define lson (o<<1)
#define rson (o<<1|1)
#define mid ((tr[o].l+tr[o].r)>>1)
struct node
{
int l,r,tmax,lmax,rmax,sum;
}tr[N<<2];
inline void pushup(node &o,node &lc,node &rc)
{
o.sum = lc.sum + rc.sum;
o.lmax = Max(lc.lmax,lc.sum+rc.lmax);
o.rmax = Max(rc.rmax,rc.sum+lc.rmax);
o.tmax = Max( Max(lc.tmax,rc.tmax) , lc.rmax+rc.lmax );
}
inline void pushup(int o)
{
pushup(tr[o],tr[lson],tr[rson]);
}
inline void build(int o,int l,int r)
{
tr[o].l = l; tr[o].r = r;
if (l==r)
{
tr[o].tmax = tr[o].lmax = tr[o].rmax = tr[o].sum = val[l];
return;
}
build(lson,l,mid);build(rson,mid+1,r);
pushup(o);
}
inline node query(int o,int l,int r)
{
if (l<=tr[o].l && tr[o].r<=r) return tr[o];
node left={0,0,-inf,-inf,-inf,-inf},right={0,0,-inf,-inf,-inf,-inf},res;
if (l<=mid) left = query(lson,l,r);
if (r>mid) right = query(rson,l,r);
pushup(res,left,right);
return res;
}
#undef lson
#undef rson
#undef mid
- 主函数
inline void Case_Test()
{
cin>>n>>m>>k;
cin>>a;
sam.init();
for (int i=0;i<n;i++)
sam.extend(a[i]-'a');
for (int i=1;i<=m;i++)
cin>>val[i];
build(1,1,m);
while (k--)
{
cin>>b;
ans = 0;
solve();
}
}
