比赛过去两天才总结本场比赛(因为新的牛客3今天打完了)。本场比赛来看还是不错的,短暂的成为了“一队”哈哈,这归功于我们在216min~218min开出了两题,并且最后257min过了J,从签到完毕之后到218min整整坐了3h的牢...幸好没有放弃,我和zyx一直开H,伍教练一直开D,结果还是好的,不过K这个dp没写出来...补题吧
G.Link with Monotonic Subsequence(构造/签到)
题意:给你一个$n$,你需要构造一个$n$的排列p 使得这个max(lis(p),lds(p)) 最小 ,也就是说我不仅要求最长上升子序列(lis)最小,还要求最长下降子序列(lds)最小,求输出构造的排列p,print any
思路:我们需要都尽量可能小,假设现在n=9,最极端情况当然就是1,2,3,4,5,6,7,8,9,这时候lis=9,lds=1,所以我们尝试交换一下,使9,1往中间靠。那么就应该是[3,2,1],[6,5,4],[9,8,7]这样的时候lis=3,lds=3,因为每次都只在其中一块选出一个,如果刚刚比9多一个怎么办?例如n=10,这时候放最后一个即可。所以是[3,2,1],[6,5,4],[10,9,8,7]。
所以答案$ans = \left \lceil \sqrt{n} \right \rceil $,划分ans个区域每块逆序输出即可。
代码:代码有些丑
inline void Case_Test()
{
cin>>n;
k = sqrt(n);
if (k*k<n) k++;
for (int i=1;i*k<=n;i++)
for (int j=i*k;j>(i-1)*k;j--)//每次逆序输出
cout<<j<<" ";
int res = n%k;//剩余的
for (int i=n;i>=n-res+1;i--)
cout<<i<<" ";
cout<<endl;
}
J.Link with Arithmetic Progression(最小二乘法)
题意:给你$n$个数$a_i$,求将其修改为等差数列的最小代价,代价就是$\Sigma_{i=1}^n(a_i-a_i^\prime )^2$。也就是对其进行修正,最后求类似于偏差的值。
思路:其实就是最小二乘法,给你若干个离散的点$(i,a_i)$,求一条直线(这条直线上的点肯定是等差数列),最后的代价就是点到直线对应点距离的平方。
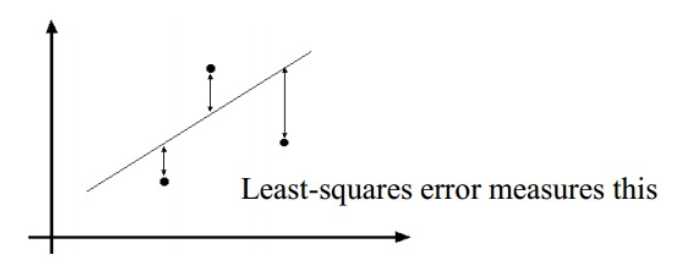
直线拟合
代码:
class LeastSquare{
double a, b;
public:
LeastSquare(const vector<double>& x, const vector<double>& y)
{
double t1=0, t2=0, t3=0, t4=0;
for(int i=0; i<x.size(); ++i)
{
t1 += x[i]*x[i];
t2 += x[i];
t3 += x[i]*y[i];
t4 += y[i];
}
a = (t3*x.size() - t2*t4) / (t1*x.size() - t2*t2);
b = (t1*t4 - t2*t3) / (t1*x.size() - t2*t2);
}
double getY(const double x) const
{
return a*x + b;
}
void print() const
{
cout<<"y = "<<a<<"x + "<<b<<"\n";
}
double calc(const vector<double>& x, const vector<double>& y)
{
double res = 0;
for (int i=1;i<=n;i++)
{
double t = a*i+b;
res += (t-y[i-1])*(t-y[i-1]);
}
return res;
}//计算答案
};
inline void Case_Test()
{
cin>>n;
ans = 0;
vector<double> x,y;
for (int i=1;i<=n;i++)
{
x.push_back(i);
cin>>k;
y.push_back(k);//点(i,k)
}
LeastSquare ls(x,y);
cout<<fixed<<setprecision(10)<<ls.calc(x,y)<<endl;
}
D.Link with Game Glitch(二分+最短路SPFA)
题意:$n(2\leq n\leq 1000)$种物品,$m(2\leq m\leq 2000)$个配方,$a$个$b$物品可以制作$w\times c$个$d$物品,问任何人都不能换到无穷多的物品的最大$w$是多少
思路:这个题很容易想到判环。
题意可以这么来看,从b到d有一条路,边权是$\frac{w\times c}{a}$,如果是连乘的话最后可能会很大,所以我们同时取$log$,则有$log(\frac{w\times c}{a}) = log(w\times c)-log(a)$,这样乘法就变成了加减法。
又因为每次边权不一样,所以我每次重新建边,实际上可以建一次每次按照1..m修改边权即可。
for (int i=1;i<=m;i++)
add(in[i].b,in[i].d,log(x*in[i].c)-log(in[i].a));
一开始所有点都入队,没有起点,每一个都是起点。标志数组全部一开始标记为1,并且dis全部赋值-inf,我这里写的是-1e9。
然后跑一遍SPFA,这个可以判正环(在SPFA的基础上判断入队列次数是否超过n即可)。
代码:
inline bool SPFA(double x)
{
for (int i=1;i<=n;i++)
{
head[i] = 0;
vis[i] = 0;
dis[i] = -1e9;
cnt[i] = 0;
}
cnte = 0;
for (int i=1;i<=m;i++)
add(in[i].b,in[i].d,log(x*in[i].c)-log(in[i].a));
queue<int> Q;
for (int i=1;i<=n;i++)
{
Q.push(i);
vis[i] = true;
}
while (!Q.empty())
{
int u=Q.front();Q.pop();
vis[u]=false;
for (int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
double w=edge[i].w;
if (dis[v]<dis[u]+w)
{
dis[v]=dis[u]+w;
cnt[v] = cnt[u] + 1;
if (cnt[v]>=n) return false;//成环了
if (!vis[v]) {Q.push(v);vis[v]=true;}
}
}
}
return true;
}
inline void Case_Test()
{
cin>>n>>m;
for (int i=1;i<=m;i++)
cin>>in[i].a>>in[i].b>>in[i].c>>in[i].d;
double l = 0, r = 1;
while (r-l>eps)
{
double mid = (l+r)/2.0;
if (SPFA(mid))//如果可以,则答案还可能大,继续让l往右边找
l = mid;
else
r = mid;
}
cout<<fixed<<setprecision(10)<<l<<endl;
}
H.Take the Elevator(multiset+贪心)
题意:给你三个数$n,m,k$,表示有$n$个人需要乘坐电梯,每趟电梯有$m$个人,电梯最高位$k$层(这个条件没什么用)。接下来给出$n$个人的起始点与目的地$(a_i,b_i)$,电梯只可以在第一层由下转为上,其他时候都可以转换。求将所有人送到目的地需要的时间是多少。
思路:最主要的思想就是把这些人看成若干个竖着的线段,然后理解到上升跟下降其实是一样的,所以这里只考虑上升的先(容易画图),写好一种情况,另一种情况只需要cv即可。
先将其进行排序,目的地高的贪心优先判断,这里每一趟最多有m个竖线,不是线段的原因是有可能有空隙拼接,例如1->2,5->9这样也可以的。所以每条线判断的时候,需要判断能否继承上面一条线段的下面,例如当前已经有5->9的话,后面来的1->2就可以接在下面。
例如下面的情况,n=5,m=2,一共有5个人:
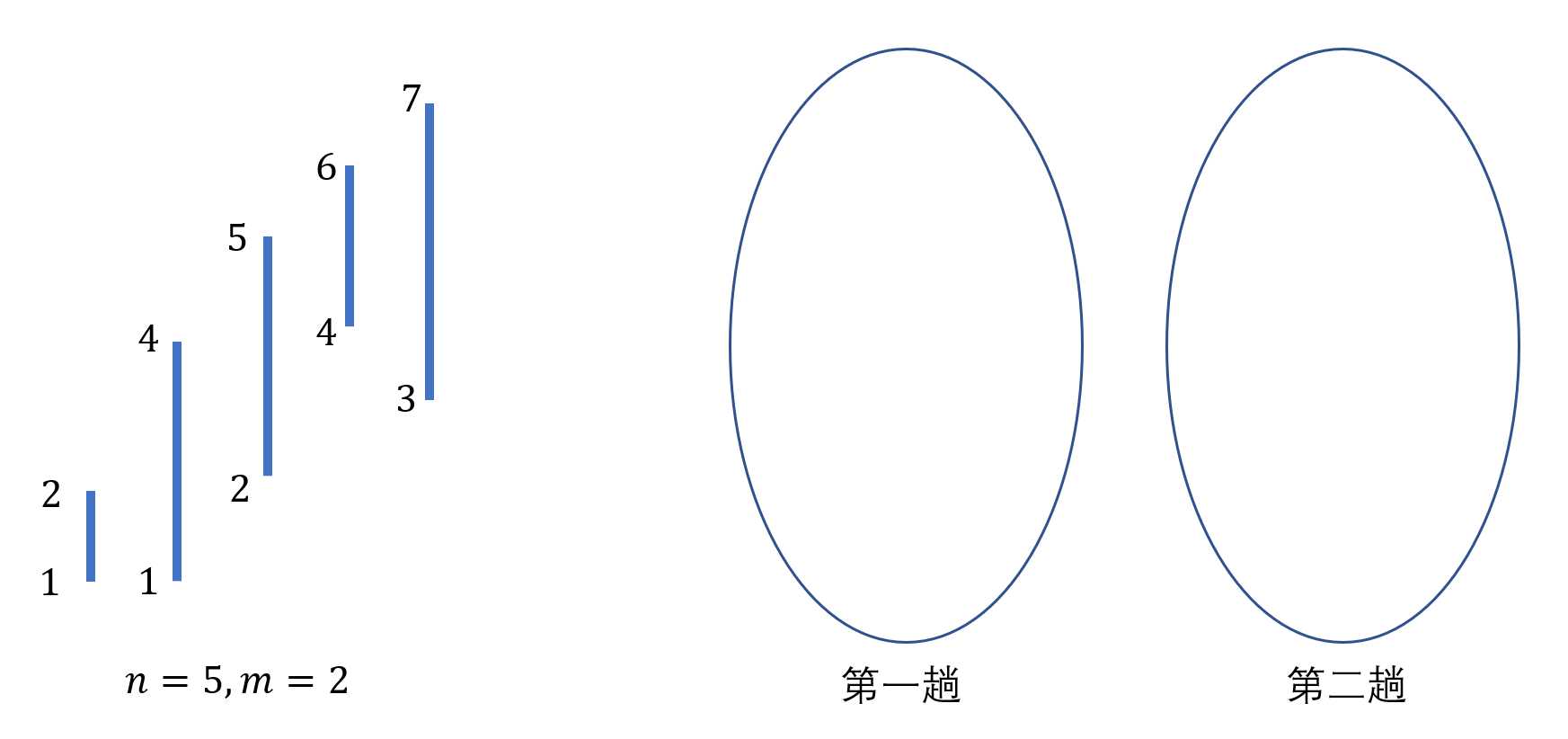
m=2表示每一趟最多有两条竖线
此时先判断需要进入的第一条线3->7这一条。
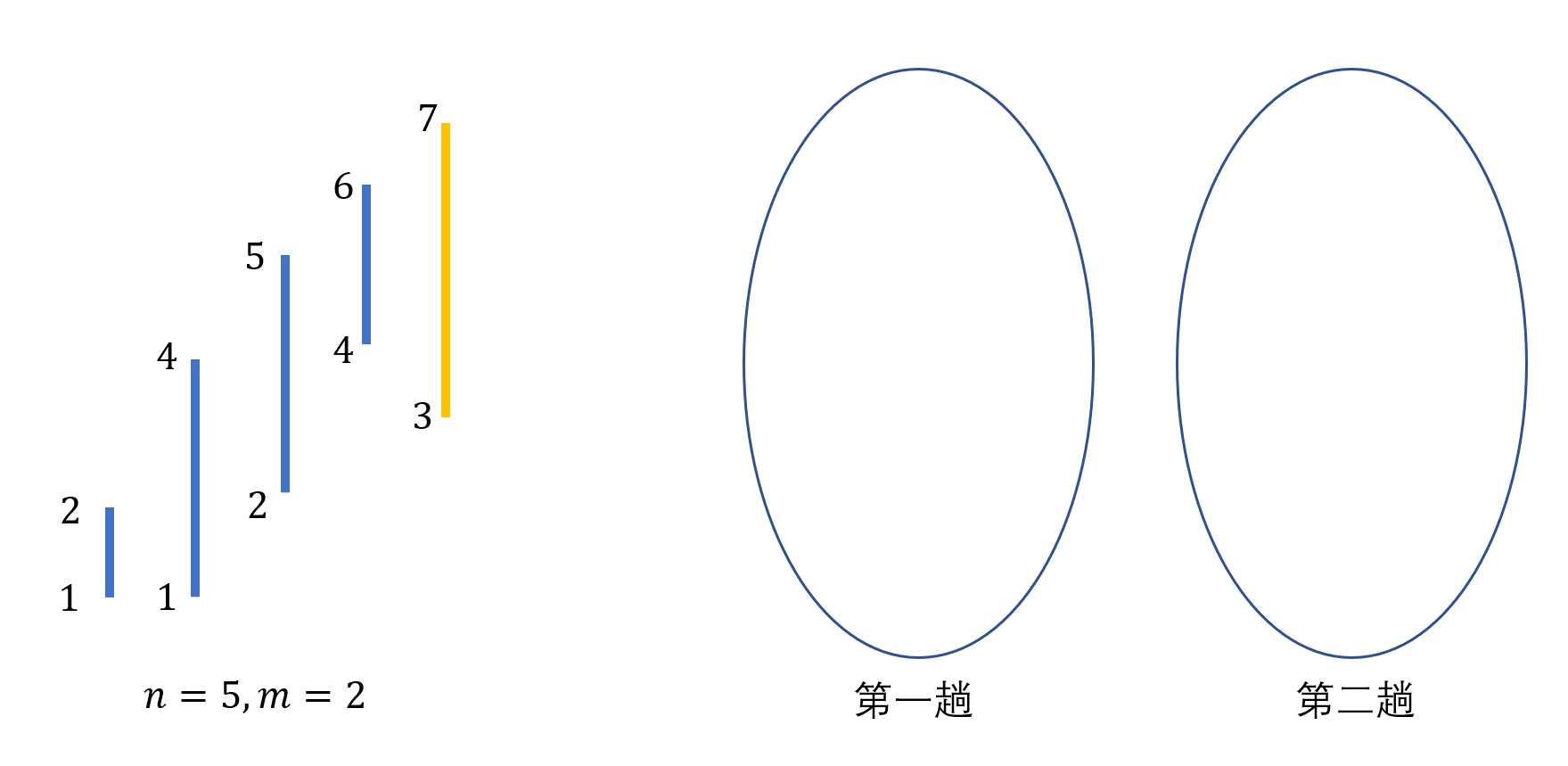
首先判断这条线是否能够继承上面的线,没有则新开一条线。
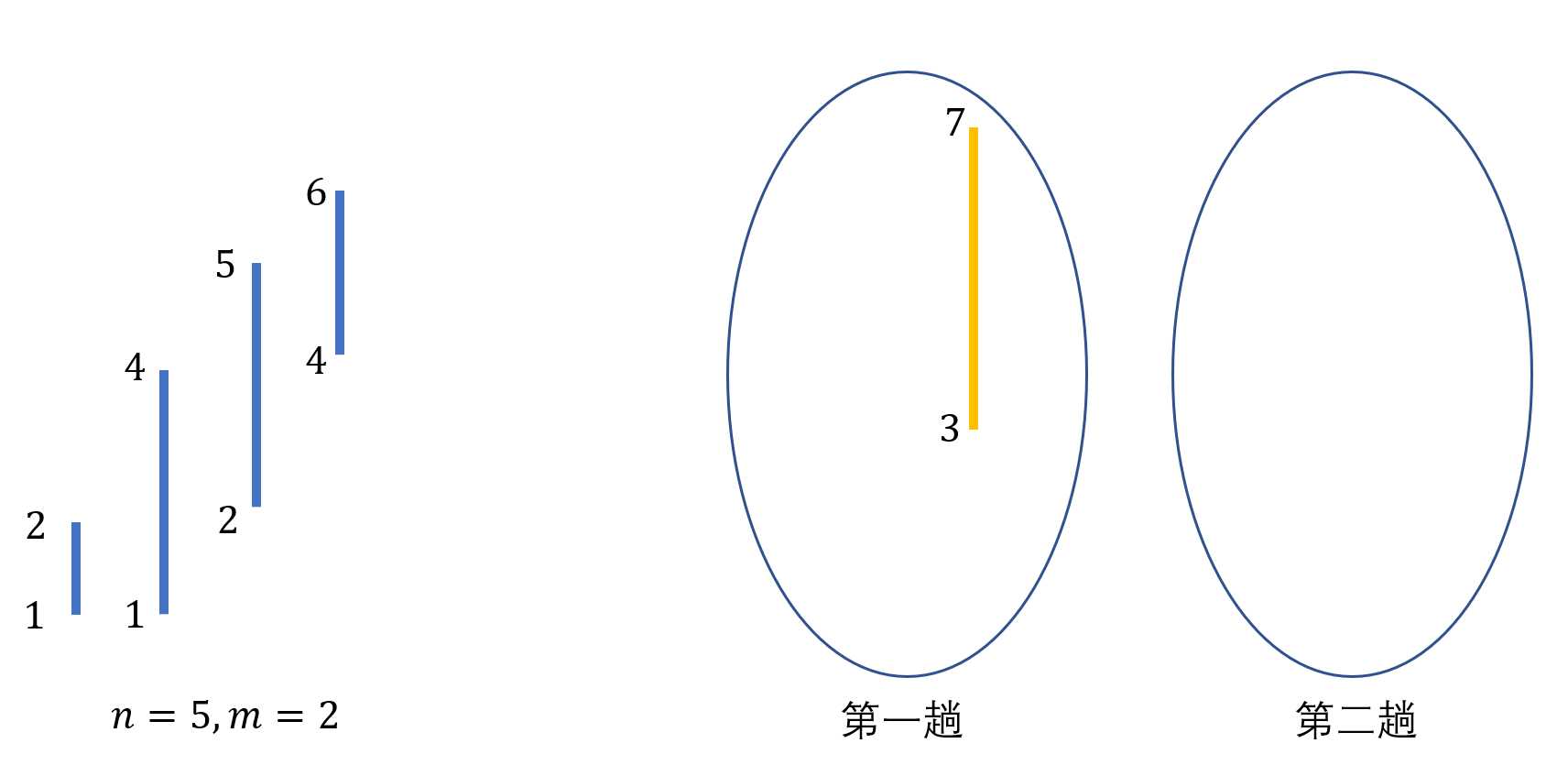
这时候multiset中已经有一条线
现在4->6进来这条线可以同样判断,无法继承原有的,所以判断第一趟是否满了,没满则进入第一趟中。
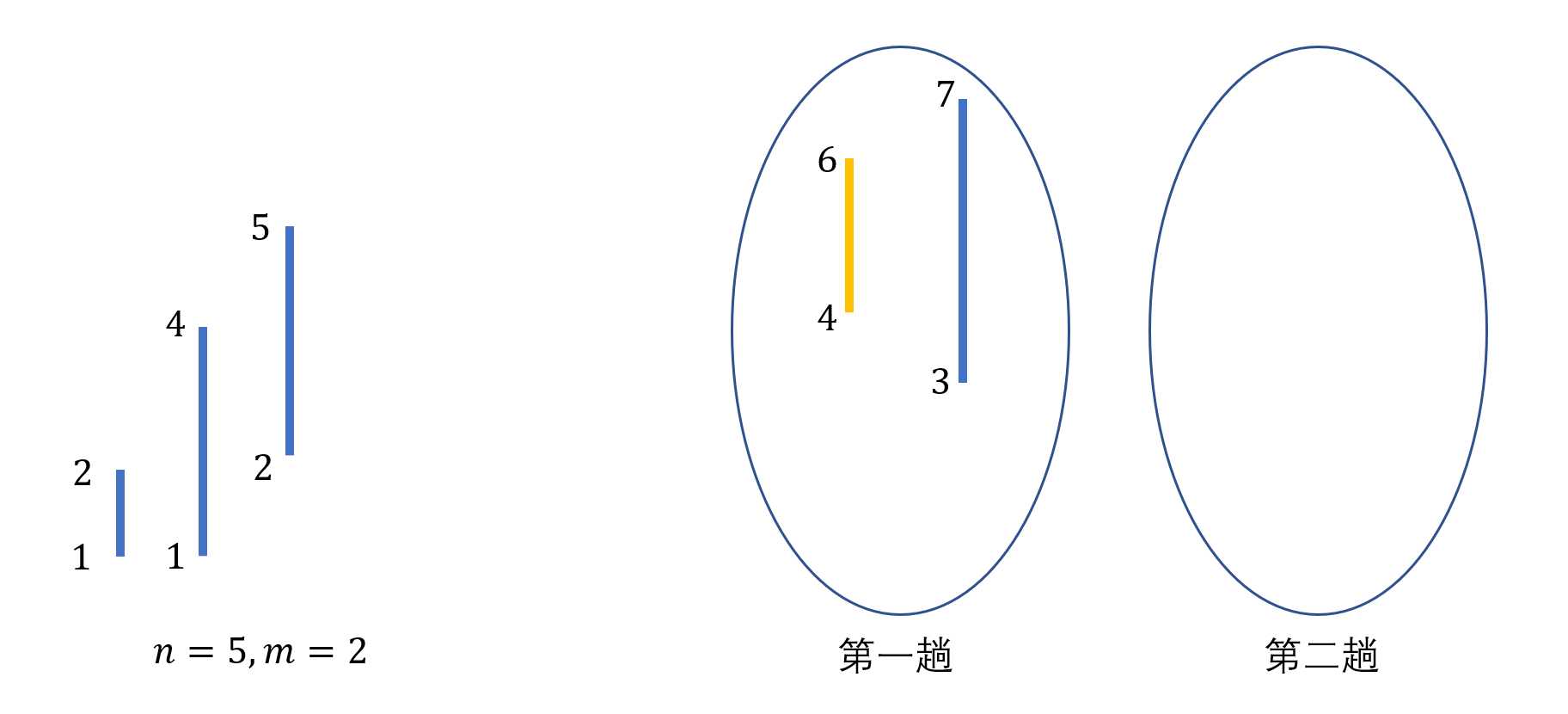
4->6也没有找到可以继承的,且第一趟也可以进,multiset新开一条
同样,后面两条线发现无法继承,所以在第二趟中新开进入。
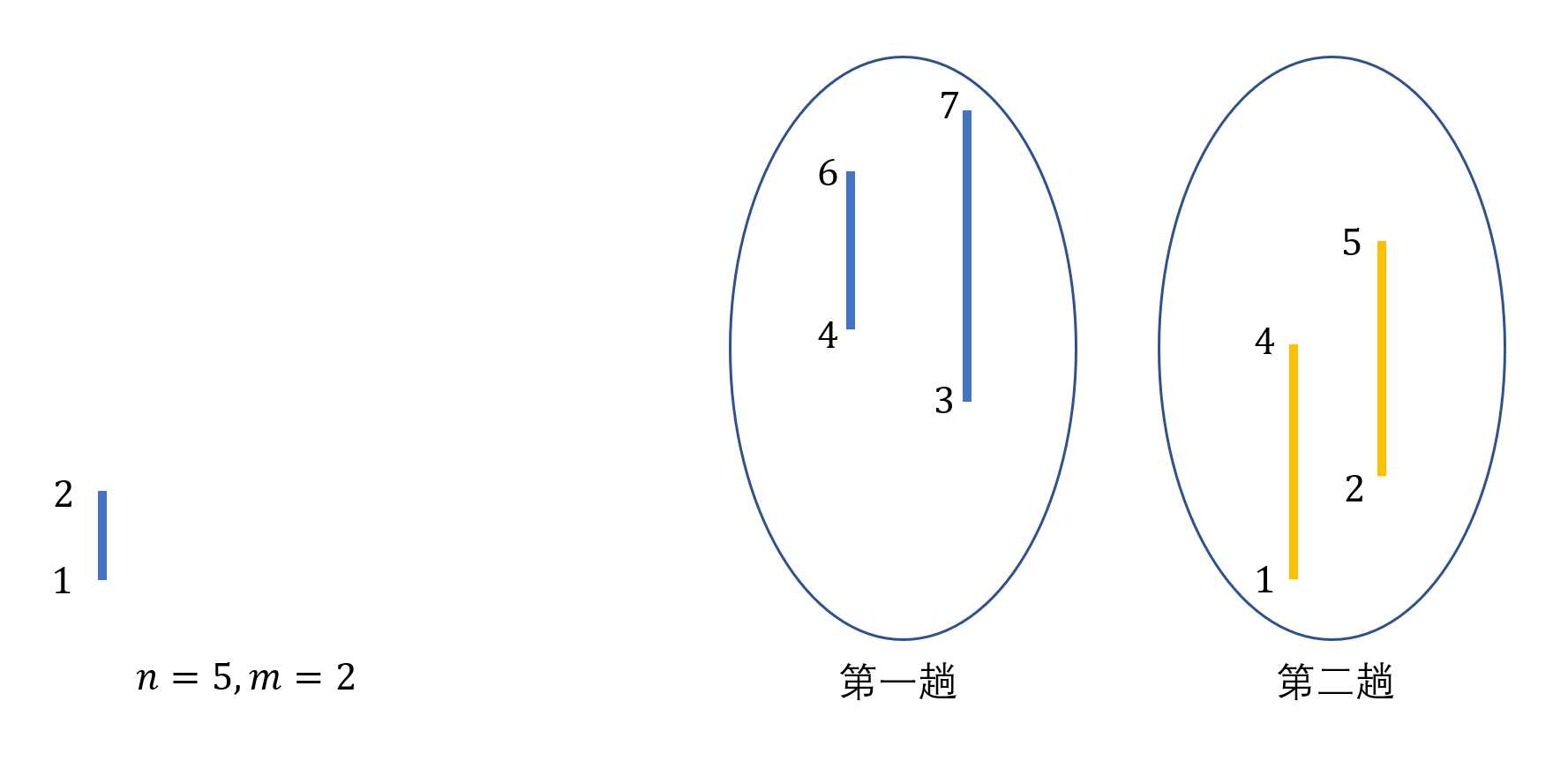
在第一趟中挤不进去,则在第二趟进入
重点来了,接下来这条1->2可以继承,首先在multiset中进行二分(稍后细讲),这时候发现第一条进入的线(id=1)是可以塞入的,实际上也可以理解,可以1->2先进入,然后在2楼下,3->7再进入。
那么就在multiset中删去 3->7原有的这条线段,现在由1->2 继承。
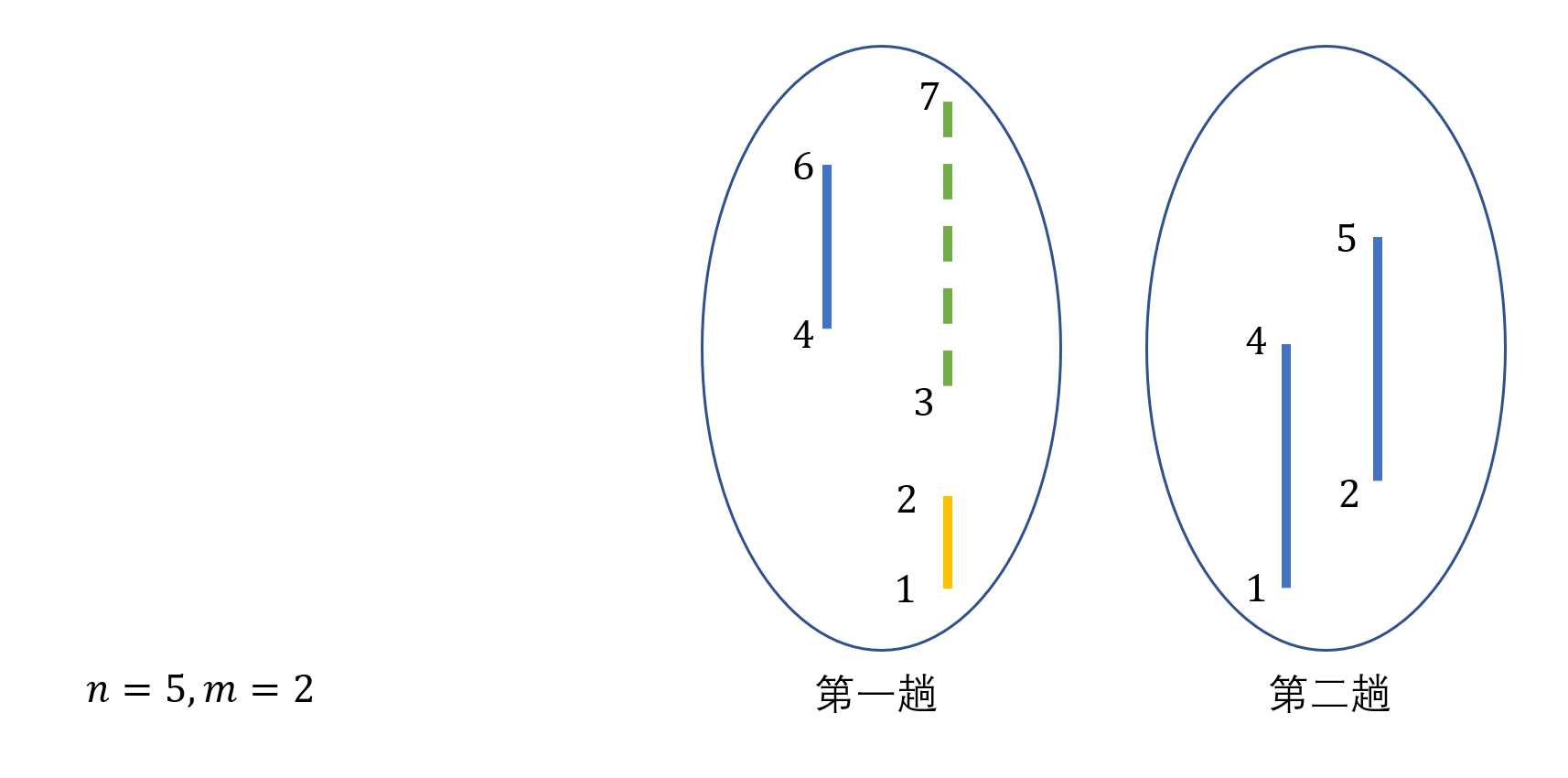
删去原有的线,更新为现在的新线
for (int i=1;i<=cnt1;i++)//遍历每一个上升的线段
{
auto t = st.lower_bound({a[i].h,0});//在st中二分
if (t==st.end())//不能在已有的情况下继承
{
if (num[cnt]==m)//如果第cnt趟满了
cnt++;//则重新开一趟
p[cnt] = Max(p[cnt],a[i].h);//当前存一下最高达到的层数
num[cnt]++;//这一趟人数+1
st.insert(seg(a[i].d,cnt));//将这个线段的最下点存入
}
else//能够继承
{
int id = t->id;
st.erase(t);//删去原有的线段
st.insert(seg(a[i].d,id));//将新的线段存入
}
}
现在来讲一下二分。
首先我线段的最下端我用的是.d,最上端我用的是.h。从上图可以看出,我每次只需要查找是否线段的下端是否比我当前线段的最高点要大。
所以我的这个multiset存入的是seg结构体,multiset<seg> st,s;。
而seg结构体一共两个值,x是存入set中的线段的最低端,id存的是当前线段的编号,例如上图的3->7存的是1,1->2继承的也是1。
struct seg
{
int x,id;
seg(int _x,int _id):x(_x),id(_id){}
bool operator < (const seg& rhs) const{
if (x==rhs.x)
id<rhs.id;
return x<rhs.x;
}//需要定义<符号 set是有序的
};
这样两边结束之后我可以得到长度为res1的p数组(表示上升的最大值),还有res2的q数组(表示下降的最大值),哦对了,下降的处理例如一条线是7->4我交换看成4->7,然后cv一份。
p[i]表示的是第i趟最高要去的地方,q[i]也是同样的。这时候for一遍统一一下二者的max即可,这个简单。
for (int i=1;i<=Max(res1,res2);i++)
ans += 2*(Max(p[i],q[i])-1);
cout<<ans;
代码:
struct node
{
int d,h;
}a[N],b[N];
struct seg
{
int x,id;
seg(int _x,int _id):x(_x),id(_id){}
bool operator < (const seg& rhs) const{
if (x==rhs.x)
id<rhs.id;
return x<rhs.x;
}
};
multiset<seg> st,s;
int num[N];
inline void Case_Test()
{
cin>>n>>m>>k;
for (int i=1;i<=n;i++)
{
int x,y;
cin>>x>>y;
if (y<x)
{
b[++cnt2].d = y;
b[cnt2].h = x;
}//下降
else
{
a[++cnt1].d = x;
a[cnt1].h = y;
}//上升
}
sort(a+1,a+cnt1+1,[](node a,node b){
if (a.h==b.h) return a.d>b.d;
return a.h>b.h;
});
int cnt = 1;
for (int i=1;i<=cnt1;i++)
{
auto t = st.lower_bound({a[i].h,0});
if (t==st.end())//不能在已有的情况下继承
{
if (num[cnt]==m)
cnt++;
p[cnt] = Max(p[cnt],a[i].h);
num[cnt]++;
st.insert(seg(a[i].d,cnt));
}
else//能够继承
{
int id = t->id;
st.erase(t);//删去原有的线段
st.insert(seg(a[i].d,id));//将新的线段存入
}
}
int res1 = cnt;//存储一下有多少条
sort(b+1,b+cnt2+1,[](node a,node b){
if (a.h==b.h) return a.d>b.d;
return a.h>b.h;
});
for (int i=1;i<=cnt;i++) num[i] = 0;
cnt = 1;
for (int i=1;i<=cnt2;i++)
{
auto t = s.lower_bound({b[i].h,0});
if (t==s.end())//塞不进去 不能继承
{
if (num[cnt]==m)
cnt++;
q[cnt] = Max(q[cnt],b[i].h);
num[cnt]++;
s.insert(seg(b[i].d,cnt));
}
else
{
int id = t->id;
s.erase(t);
s.insert(seg(b[i].d,id));
}
}
int res2 = cnt;//同上,存储
for (int i=1;i<=Max(res1,res2);i++)
ans += 2*(Max(p[i],q[i])-1);
cout<<ans;
}