2022"杭电杯"中超联赛·第八场

签到签慢了，四题中间的样子吧，然后难题也没有写出来，补了两题，好像02也能补，再说吧哈哈。

1004.Quel'Thalas（签到）

题意：给你一个$[0,n]\times [0,n]$的二维点，用一条直线去划，最少用多少条线通过区域内除了$(0,0)$的点。

思路：我的想法是划斜线，队友的想法是横竖，结果都是一样的——$2\times n$

1001.Theramore（思维+签到）

题意：给你一个01字符串，你可以选择一个奇数区间 $[l,r]$ 使得区间内的01反转过来，可以使用无限次，求最后的字典序最小的字符串。

思路：每次就交换长度为$3$的区间，这样每次就是将$1$往后移动（同样在奇数位上），所以只需要统计奇偶的1有多少个。

这个是什么意思呢？说明这些1可以放在后面开始放，但是同样也需要满足奇偶，奇数的1只能放在奇数上，偶数的1只能放在偶数上。

所以统计完之后从后往前放就好，如果当前还有则放。

代码：

inline void Case_Test()
{
    int r[2];
    r[0] = 0, r[1] = 0;
    cin>>s;
    n = s.size();
    for (int i=0;i<n;i++)
    {
        if (s[i]=='0') continue;
        r[i%2]++;
    }
    string ans(n,'0');
    for (int i=n-1;i>=0;i--)
        if (r[i%2]) ans[i] = '1', r[i%2]--;//往前放，如果还有那么就放
    cout<<ans<<endl;
}

1011.Stormwind（签到）

题意：给你一个$n\times m$的纸片以及一个$k$，求最多能砍多少刀并且保证每一块的面积都需要大于等于$k$，注意：每一刀都需要保证是二维坐标的整数点，并且起点和终点都需要在边缘上（不能中间砍）

思路：枚举$a$，这个表示的是小长方形的横着的那条边，从1到n进行枚举，如果不能正好整除，多出来怎么办？例如下图：

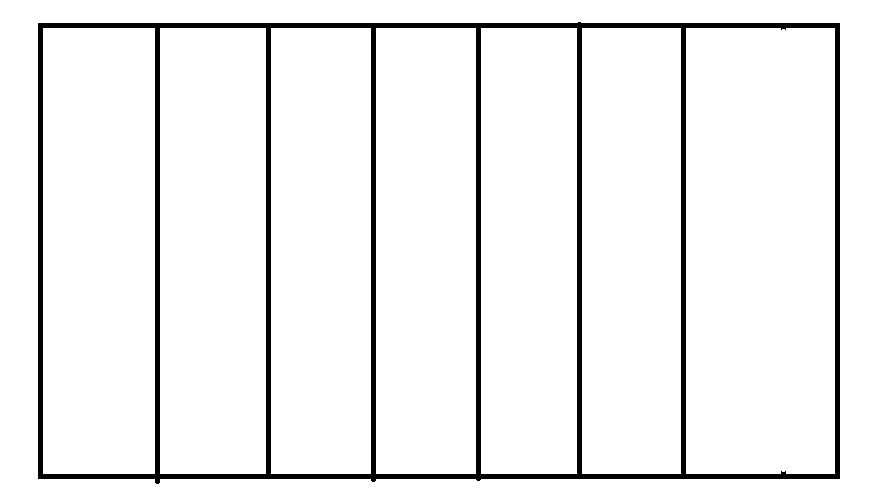
右侧大于a，多出来一块

我本来想着是判断一下，结果把它看成左侧一样的，只不过它多出来一块就行，其实就是不管它，那么这样竖着首先能切n/a-1刀。

那么横着的也是同理，不过需要先要得到我小长方形的另外一条边长是多少，需要向上取整就是t=(k+a-1)/a，还是按照上面方法，加起来取Max就好。

代码：

inline void Case_Test()
{
    cin>>n>>m>>k;
    ans = 0;
    for (int a=1;a<=n;a++)
    {
        int res = 0;
        if (a*m<k) continue;
        res = n/a-1;
        int t = (k+a-1)/a;
        res += m/t-1;
        ans = Max(ans, res);
    }
    cout<<ans<<endl;
}

1008.Orgrimmar（树形DP）

题意：给你一颗树，求一个点集其中的点最多只与一个点相连的集合。求集合内点的最大个数。

思路：设置三种状态(用u表示当前点，用v表示子结点)

dp[u][0]：不删u点。u只与一个v相连，其他都不连。
dp[u][1]：不删u点。u都不与任何v相连。
dp[u][2]：删u点。

那么来看三种状态转移：

dp[u][0]：只能与一个v相连，说明要选择v未选择别人的（因为如果选了再连u就三个点连续了，不合题意），所以需要选择v的dp[v][1]，其他的点则都不能连，则选择dp[v][2]。那么如何选择这个v呢？很显然当dp[v][1]-dp[v][2]最大的时候，这个是最优的。
dp[u][1]：都不连v，这个意思代表不删u，删v，所以只需要加上所有的dp[v][2]。
dp[u][2]：需要删u，这个最自由，对于每一个v的三种状态选Max即可。

代码：

int dp[N][3];
inline void dfs(int x,int pre)
{
    int r2 = 0, r0 = 0, r1 = 0, res = 0,p = 0,t = 0;
    //debug2(x,pre);
    for (int i=head[x];i;i=edge[i].next)
    {
        int y = edge[i].to;//注意一定写int y,保证在内部有效。
        if (y==pre) continue;
        dfs(y,x);
        res += dp[y][2];
        if (dp[y][1]-dp[y][2]>p) p = dp[y][1]-dp[y][2],t = y;
        r2 += max({dp[y][0],dp[y][1],dp[y][2]});
    }
    dp[x][0] = 1 + Max(res - dp[t][2] + dp[t][1], res);
    dp[x][1] = 1 + res;
    dp[x][2] = r2;
}
inline void Case_Test()
{
    for (int i=1;i<=n;i++) head[i] = dp[i][0] = dp[i][1] = dp[i][2] = 0;
    cnt = 0;
    cin>>n;
    for (int i=1;i<n;i++)
    {
        cin>>x>>y;
        add(x,y);
        add(y,x);
    }
    int st=1;
    dfs(st,0);
    cout<<max({dp[st][0],dp[st][1],dp[st][2]})<<endl;
}

1007.Darnassus（思维+最小生成树）

题意：给你$n(1\leq n\leq 50000)$的点以及对应的$p[i]$，每个点之间的边权是$|(i-j)\times (p[i]-p[j])|$。求最小生成树。

思路：这个建完全图实在是不可能，无论从时间还是空间上来看。所以需要转化一下。
对于每个相邻的点($i,i+1$)之间的连边有：
$$
|(i+1-i)\times (p[i+1]-p[j])\ =\ |p[i+1]-p[i]| \leq n-1
$$

这$n-1$条边已经足够满足生成一颗生成树了，但是不一定是最小的，所以我们能得到什么信息呢？

如果一条边长度大于等于$n$则是不行的，所以我们只需要找到小于等于$n-1$的边即可。

那么如何枚举？从上面那个式子来看
$$
w=|(i-j)\times (p[i]-p[j])\leq n-1
$$

这是两个乘积，如果要满足小于$n$的话最特殊的情况是$\sqrt{n} \times \sqrt{n}$，所以只需要枚举$t=\sqrt{n}$的个数即可。

为什么呢？对于当前的$i$来说，我只需往后枚举$\sqrt{n}$个数则满足$(i-j)\leq \sqrt{n}$，这样有可能满足我们想要的条件。

那么还有其他情况吗？当然有可能，当$i-j\gt \sqrt{n}$的时候，但是我的$p[i]-p[j]\leq n$就可能满足条件。所以还需要对于$p$往后枚举$\sqrt{n}$次。

    for (int i=1;i<=n;i++)
        for (int j=i+1;j<=n&&j<=i+t;j++)
        {
            m = Abs((i-j)*(p[i]-p[j]));//边权
            if (m<=n-1) v[m].emplace_back(i,j);
            m = Abs((pos[i]-pos[j])*(i-j));//pos[p[i]] = i
            if (m<=n-1) v[m].emplace_back(pos[i],pos[j]);
        }

然后生成了所有的边，这里需要用到桶排，因为如果再进行带$\log$的排序的话则可能会超时。

最小生成树不一定需要sort，用桶排可能会优化时间

所以我把两个点加到了v[m]中。

然后跑最小生成树即可。

代码：

struct DSU {
    std::vector<int> f;
    DSU(int n) : f(n) { std::iota(f.begin(), f.end(), 0); }
    inline int leader(int x) {
        while (x != f[x]) x = f[x] = f[f[x]];
        return x;
    }
    inline bool same(int x, int y) { return leader(x) == leader(y); }
    inline bool merge(int x, int y) {
        x = leader(x);
        y = leader(y);
        if (x == y) return false;
        f[y] = x;
        return true;
    }
};
inline void Case_Test()
{
    cin>>n;
    vector<vector<PII>> v(n);
    DSU dsu(n+1);
    for (int i=1;i<=n;i++)
    {
        cin>>p[i];
        pos[p[i]] = i;
    }
    int t = sqrt(n);
    for (int i=1;i<=n;i++)
        for (int j=i+1;j<=n&&j<=i+t;j++)
        {
            m = Abs((i-j)*(p[i]-p[j]));
            if (m<=n-1) v[m].emplace_back(i,j);
            m = Abs((pos[i]-pos[j])*(i-j));
            if (m<=n-1) v[m].emplace_back(pos[i],pos[j]);
        }
    ans = 0;
    cnt = 0;
    for (int i=0;i<=n-1;i++)
    {
        for (auto e:v[i])
        {
            int u = e.first, v = e.second;
            if (dsu.same(u,v)) continue;
            dsu.merge(u,v);
            ans += i;
            cnt++;
            if (cnt==n-1) {cout<<ans<<endl;return;}
        }
    }
}