这一场打的很烂,队友一直在开计算几何没有做出来,而我也不会做,最近被好几场比赛压着了,所以我还是简短的写一下题吧,补题等到后面再说吧。

1006 Maex(树形DP)
题意:给你一个$n$个点的树,求每一个结点包括其子树的$MEX$值的和的最大值。
思路:对于一个子树来看,通过对于$MEX$的理解,如果没有出现$0$那么值一直为$0$,所以我们想要填$0$。那么填完之后应该填什么?应该填$1$...我想要求出最大值,那么肯定是想要$0$在最底下,然后让上面的都可以利用它,这样就是一个最长链了。那么就求深度然后得到最长链填$0$吗,如果子树的其他支链有什么关系呢?我们来看下面这个图:
这张图可以对比两种:左边是最深链,右边是多链
我们对其分别进行计算,发现并不是最深链,还需要看其他支链。原因是我虽然链少,但是我可以通过其他子结点来堆,使得我的当前结点变高,例如这个四个父亲的结点$6$,因为子结点很多,它的$MEX$可以很大。
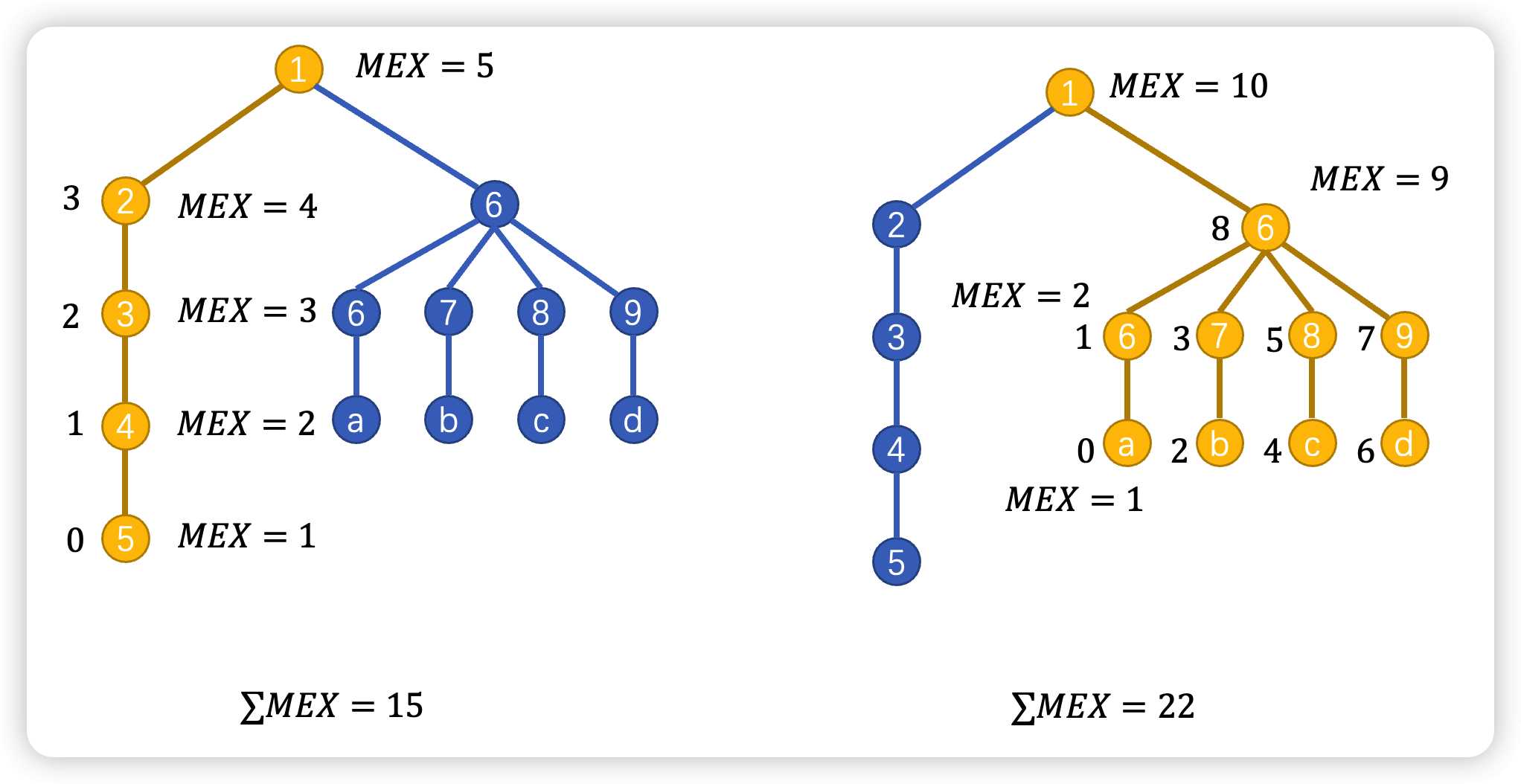
左边是最深链,右边是多链.很明显,不能只看最深链
所以我们需要维护两个值,一个是子结点个数,这样来看加上子结点个数就是自己的$MEX$值,然后每次加上儿子结点的$Max$值即可。
代码:
inline void dfs(int x,int pre)
{
num[x] = 1;//首先肯定得有自己
int res = 0;
for (int i=head[x];i;i=edge[i].next)
{
int y = edge[i].to;
if (y==pre) continue;
dfs(y,x);
res = Max(res, f[y]);
num[x] += num[y];//维护子结点个数
}
f[x] = res + num[x];//维护当前答案
}
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++) head[i] = 0;
cnt = 0;
for (int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
dfs(1,0);
cout<<f[1]<<endl;
}
1012 Loop(链表)
题意:给你一个长度为$n$的序列,你可以进行$k$次操作,选择一个数让其放到后面的任意位置(可以不动),求操作结束后的最大序列(字典序最大)。
思路:经过推断,可以先求出逆序对,例如$[4,3,1,2]$那么说明如果有机会我们需要将$1$放到$2$的后面使其变成$[4,3,2,1]$。这样就能保证字典序最大。
那么如果有多个逆序对怎么办呢?例如$[4,5,1,2,7,6,5,7]$,图中有$[1,2],[2,7],[5,7]$三对逆序对,我们需要交换最大的$[5,7]$吗?不是,我们需要交换最前面的$[1,2]$,因为字典序是从前往后的,所以前面的满足条件的话当然是最大的。
那么相当于我取出来两个数,接下来如何看?例如上面那个例子,我取出$[1]$实际上现在应该看$[4,5,2,7,6,5,7]$这个时候要比较$2$两端的,所以我们需要用$O(1)$的链表来做。
inline void remove(int cur)
{
vis[cur] = 0;
r[ l[cur] ]=r[cur];
l[ r[cur] ]=l[cur];
int x = l[cur], y = r[cur];
if (a[x]<a[y]) q.push(x);//又产生逆序对
}
所以我们用一个优先队列来存放每次的最前面的,每次取出来的就是最前面的。
那么取出来的数放在哪呢?
放在最后第一个降序的地方,一次往前面插,对于当前的数,把大于它的插前面,这样保证字典序最大,例如现在变成$[3,4,5,7,\underline{3},1]$,现在取出来了$[4,3,2]$那么将$4$放在$3$前面,$3,2$放在$1$前面。
int l[N],r[N];
priority_queue<int,vector<int>,greater<int>> q;
priority_queue<int> num;
inline void remove(int cur)
{
vis[cur] = 0;
r[ l[cur] ]=r[cur];
l[ r[cur] ]=l[cur];
int x = l[cur], y = r[cur];
if (a[x]<a[y]) q.push(x);
}
inline void Case_Test()
{
cin>>n>>k;
vector<int> ans;
while (!q.empty()) q.pop();
for (int i = 1; i <= n ;i++)
{
l[i] = i-1, r[i] = i+1;
cin>>a[i];
vis[i] = 1;
}
a[0] = inf, a[n+1] = -inf;
r[0] = 1, l[n+1] = 1;
l[1] = 0, r[n+1] = 0;
for (int i=1;i<=n;i++)
if (a[i]<a[i+1])
q.push(i);//首先计算逆序对,进队等待操作
while (k--)
{
if (q.empty()) break;
int cur = q.top();q.pop();//取出进行链表操作
remove(cur);
num.push(a[cur]);
}
int pos = n+1, pre = 0;
for (int i=1;i<=n;i++)
{
if (!vis[i]) continue;
if (a[i]<pre) {pos = i;break;}
else
{
ans.push_back(a[i]);
pre = a[i];
}
}
for (int i=pos;i<=n;i++)
{
if (!vis[i]) continue;
while (!num.empty() && num.top()>a[i])
{
ans.push_back(num.top());
num.pop();
}
ans.push_back(a[i]);
}
while (!num.empty())
{
ans.push_back(num.top());
num.pop();
}//还没有插完
for (int i=0;i<ans.size();i++)
cout<<ans[i]<<" \n"[i+1==ans.size()];
}
