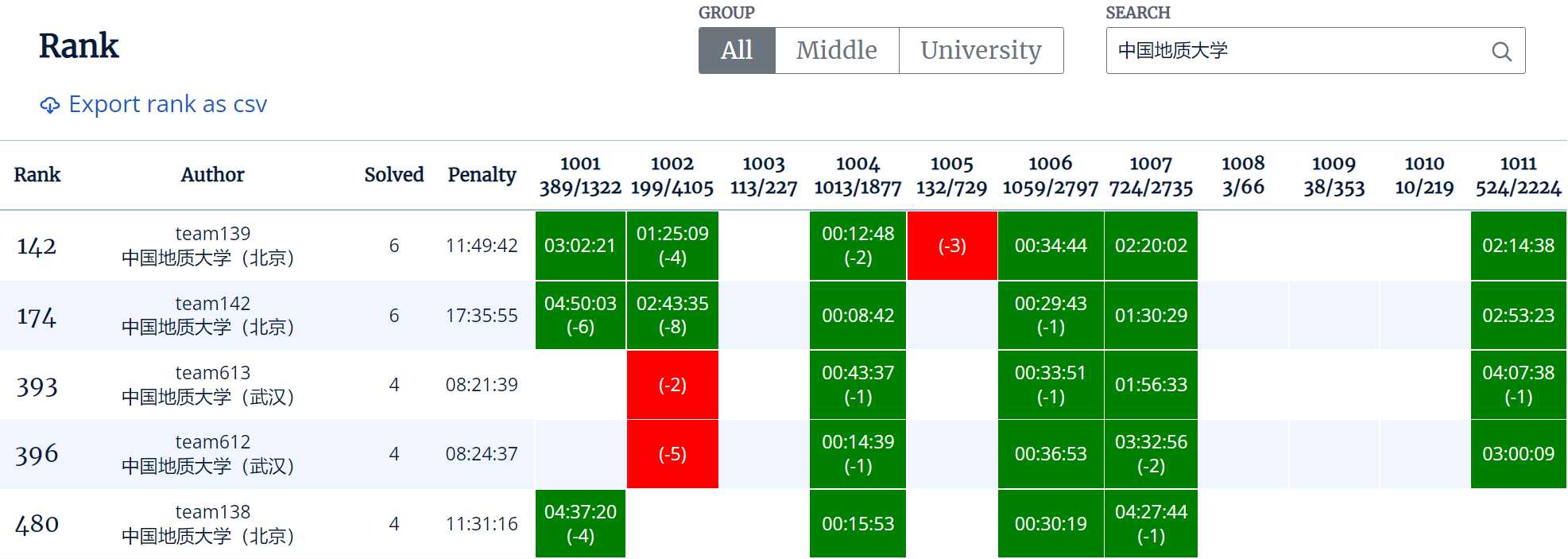
这场全队怒A6题,排名来到174名,去掉中学生排名来到86,还不错噢。
签到签的还算快,02卡时过的哈哈,11是一个板子题,01是一个逆天dp...
1004.Link with Equilateral Triangle(签到)
题意:给你一个边长为$n$的三角形,左侧不能填0,右侧不能填1,下边不能填2,对于每一个小三角形都不能是3的倍数,求是否可以构造出一个这样的三角形。
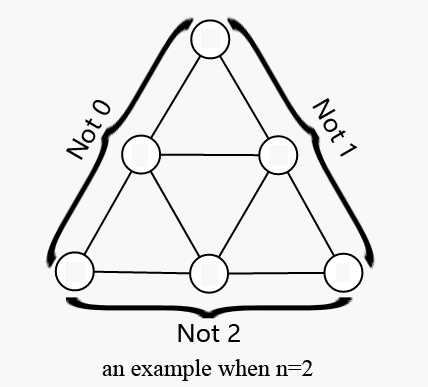
左侧不能填0,右侧不能填1,下边不能填2
思路:大胆猜测一直是No,然后自己不敢交,手推了n=3的时候好像不行,所以直接大胆猜测交一发AC了。
对于一个合法的解,应当满足不存在同时包含
0,1,2的三角形,下面我们证明这样的三角形一定存在。
左下角必然是1,右下角必然是0,底边不能含有2,则底边上必然有奇数条1-0的边,这些边都属于一个
小三角形。考虑其他的0-1边,由于不在两个斜边上,其他的0-1边必然属于两个三角形。因此“每个三角
形内0-1边的数量”的和必然为奇数。
但是,假设不存在0-1-2的三角形,则所有三角形都必然包含0条或2条的0-1边,产生了矛盾。
因此一定存在0-1-2的三角形。
代码:
inline void Case_Test()
{
cout<<"No"<<endl;
}
1006.BIT Subway(模拟)
题意:现在地铁站开始了一个票价活动,如果当前达到了100之后的就可以打八折,达到了200就可以打五折。但是你现在找一个投机取巧的方法,如果你现在198需要买10票价的,你可以拆分成2.5和7.5,你先买2.5的变成200,然后剩下的7.5就可以享受五折了。但是实际上是不允许的,求给出顺序的票价,求两种情况的价格。
思路:
直接按情况模拟即可,我这里有一个处理就是拆分之后还把他存在a[i]中,例如一开始a[i]=10,后面a[i]=7.5并且i--,这样下一次又轮到它了。
注意:exclamation: 读入double很慢,所以需要读入int类型,然后转化成double。这里读入double我tle(>1000ms),读入int最后只有78ms...
代码:
double a[N],b[N];
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>x;
a[i] = x;//一定用int读入,double读入会tle
b[i] = a[i];
}
double res1 = 0.0, res2 = 0.0;
for (int i=1;i<=n;i++)
{
if (res1<100.0)
{
if (res1+a[i]<=100.0) res1+=a[i];
else
{
a[i] -= 100.0-res1;
res1 = 100.0;
i--;
continue;
}
}
else if (res1<200.0)
{
if (res1+a[i]*0.8<=200.0) res1+=a[i]*0.8;
else
{
a[i] -= (200.0-res1)/0.8;
res1 = 200.0;
i--;
continue;
}
}
else res1 += a[i]*0.5;
}
for (int i=1;i<=n;i++)
{
if (res2<100.0) res2 += b[i];
else if (res2<200.0) res2 += b[i]*0.8;
else res2 += b[i]*0.5;
}
cout<<fixed<<setprecision(3)<<res1<<" "<<res2<<endl;
}
1007.Climb Stairs(贪心)
题意:这个题不难,队友过的
1002.Link with Running(图论)
卡时过的...
if (clock()-ti>15000/(t-2)-5) break
1011.Link is as bear(线性基)
题意:给你一个长度为$n$的数组,你选择一个区间$[l,r]$将其异或得出的答案给这些区间内的数都赋值,求最后获得最大的异或和
思路:
是个思维+结论题,可以证明,从这 $n$ 个数里任取一些数异或起来的方案,都是可以构造出对应的操作来
做到的。
所以,问题完全等价于给$n$个数,从中选一些数,使得这些数的异或和最大。
这是线性基的板题,抄一个板子即可。
下面给出证明:
- 1、如果序列里有连续的两个$0$,那么一定都可以构造出操作方案。例如 $0,0,a_1,a_2$中,比如我们要保留$a_1$不保留$a_2$ ,就可以先两次操作变成$a_1,0,0,a_2$ ,再两次操作变成$a_1,0,0,0$ ,因为上述操作总可以保证操作完后还有两个$0$,所以可以以此类推一直往下处理。如果两个$0$两边都有数字当然也没问题,我们先处理完一边儿的再回过头来处理另一边。
- 2、如果用 来表示一个需要保留的数字, 来表示一个想要删去的数字,则出现$110$ 或$011$ 的形状时,可
以通过操作删掉想删的那个数并制造出两个$0$ 。以$110$ 为例:
$$
a_1, a_2, a_3 \rightarrow a_{1} \oplus a_{2}, a_{1} \oplus a_{2}, a_{3} \rightarrow a_{1} \oplus a_{2}, 0,0
$$
就可以做到只删掉 $a_3$ 而产生两个$0$ 。
- 3、由上面$2$和$1$可以看出,只要出现$110$ 、$011$ 就可以完全解决问题,也就是出现连续两个$1$ 就完全可以构造出任意方案,而有连续的两个 也可以完全解决问题。综上,有连续两个$0$ 和连续两个$1$ 的序列,都可以造出来任意的异或方案。
- 4、所以现在唯一处理不了的就是既没有连续$0$ 也没有连续$1$ 的序列,也就是形如$01010101$ 或$1010101$ 这样的情况,这时就要用到两个数相同的条件,该条件实际上是保证了不会出现这种情况。假设相同的两个数都是$x$ ,如果最后方案里没有异或上$x$ ,则两个$x$ 的位置可以都当作$0$ 或都当作$1$ ;如果最后的方案里有异或上$x$ ,则两个$x$ 可以一个填$0$ 一个填$1$ 也可以一个填$1$ 一个填$0$ 。而上述两种情况下,$x$ 都有两种填法,且两种填法之一一定保证存在连续$0$ 或连续$1$ ,因此也可以构造出。
超级板子题:
代码:
ll p[N],x,ans;
int n;
inline void insert(ll x)
{
for (int i=62;i>=0;i--)
if (x>>i)
if (p[i])
x^=p[i];
else
{
p[i]=x;
return;
}
}
inline void Case_Test()
{
cin>>n;
for (int i=0;i<=62;i++) p[i] = 0;
ans = 0;
for (int i=1;i<=n;i++)
{
cin>>x;
insert(x);
}
for (int i=62;i>=0;i--)
if ((ans^p[i])>ans) ans=ans^p[i];
cout<<ans<<endl;
}
1001.Link with Bracket Sequence II(区间DP)
题意:给你一个$n$长度的括号序列,有$m$种括号形式,$a_i=0$表示的是可以是这$m$种任意都可以,$a_i>0$表示的是该种的左括号,$a_i<0$表示的是该种的右括号。求有多少种满足条件。
思路:定义一个f[i][j]表示区间[i,j]之间的匹配的方案数,从f[i+1][j-1]开始继承,因此i和j是分别为(和)相对的,但是可能有地方算重复(下面会讲)。
易老师这个方法很好,设置了一个g[i][j]数组,表示不可分割的数目,因为有的时候会算重复。例如样例的0 0 0 0 0 0,每次分成两个的时候确实会出现问题,比如算f[1][6]的时候,会变成枚举端点,进行两个区间相加,一开始f[1][6]+=f[1][2]+f[3][6]还有f[1][6]+=f[1][4]+f[5][6],那么这样会算重复。先来看0 0 0 0 0 0会有哪几种情况。
-
( ( ( ) ) )会被f[1][6]从f[2][5]继承。
-
( ( ) ( ) )会被f[1][6]从f[2][5]继承。
-
( ) ( ) ( )会被以下两种情况包含
-
( ) ( ( ) )会被断点分成f[1][6]+=f[1][2]+f[3][6],但是也包括了第三种情况
-
( ( ) ) ( )会被断点分成f[1][6]+=f[1][4]+f[5][6],但是也包括了第三种情况
首先来看为什么会被包含?因为( ) ( ) ( )可以看成() ()()和()() ():前者是f[1][2]+f[3][6],后者是f[1][4]+f[5][6],因为f[i][j]的定义是第i个是(,第j个是),所以这种情况都满足,算重复了,怎么办呢?
因为我们首先从f[i+1][j-1]继承而来的是不可拆分的(怎么理解这个词,就是没有经过枚举断点而来的,只是从f[i+1][j-1]继承而来的,所以是不可拆分的。
那么现在来看上面的情况为什么会被重复算,就是因为我对第二次()() ()的时候,这个f[1][4]拆分了,它包括了()(),而实际上这个已经在第一次枚举断点f[1][2]+f[3][6]被计算过了,所以我想要的这时候的f[1][4]只包含(())这种情况即可。
所以就有了这样的g[i][j]存在,它每次只继承,不枚举断点更新。我每次枚举断点保证前部分不可拆分,这样就有了顺序,不会重复。
for (int k = l+1; k<r; k+=2)
f[l][r] = (f[l][r] + 1ll * g[l][k] * f[k+1][r] % mod) % mod;
总结:
f[i][j]表示的是区间[i,j]的合法方案数.g[i][j]表示i,j一定得匹配的合法方案数,不可拆分
那么就有$f[i][j] = \Sigma _k \ g[l][k]\times f[k+1][r],\quad l\lt k\lt r$
代码:
int f[N][N],g[N][N];
inline void Case_Test()
{
cin>>n>>m;
memset(f,0,sizeof(f));
memset(g,0,sizeof(g));
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) f[i][i-1] = 1;//如果len=2开始,需要继承这里的
//例如f[2][3]需要用到f[3][2]
for (int len = 2; len <= n; len+=2)
{
for (int l = 1; l+len-1<=n; l++)
{
int r = l+len-1;
if (!a[l]&&!a[r])
f[l][r] = g[l][r] = 1ll * f[l+1][r-1] * m % mod;//匹配 [0 0]
else if ((a[l]>0&&a[l]+a[r]==0)||(a[l]>0&&a[r]==0)||(a[l]==0&&a[r]<0))
f[l][r] = g[l][r] = f[l+1][r-1];//其他匹配的情况
for (int k = l+1; k<r; k+=2)
f[l][r] = (f[l][r] + 1ll * g[l][k] * f[k+1][r] % mod) % mod;
}
}
cout<<f[1][n]<<endl;
}
我的代码多设置了一维,dp[i][j][0]表示的是题中$xAy$这种情况,也就是例如( ()() );dp[i][j][1]表示的是题中$AB$这种情况,也就是() ().
这样也不会计算重复。
int dp[N][N][3];
inline void Case_Test()
{
cin>>n>>m;
memset(dp,0,sizeof(dp));
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<n;i++)
{
if (a[i]==0&&a[i+1]==0) dp[i][i+1][0] = m;
else
{
if ((a[i]>0&&a[i]+a[i+1]==0)||(a[i]>0&&a[i+1]==0)||(a[i]==0&&a[i+1]<0))
dp[i][i+1][0] = 1;
}
}
if (n%2==1) {cout<<0<<endl;return;}
for (int k=4;k<=n;k+=2)
{
for (int i=1,j=k;j<=n;i++,j++)
{
if (a[i]==0&&a[j]==0)
dp[i][j][0] = (dp[i][j][0]+(dp[i+1][j-1][0]+dp[i+1][j-1][1])*m)%mod;
else
{
if ((a[i]>0&&a[i]+a[j]==0)||(a[i]>0&&a[j]==0)||(a[i]==0&&a[j]<0))
dp[i][j][0] = (dp[i][j][0]+dp[i+1][j-1][0]+dp[i+1][j-1][1])%mod;
}
for (int d=1;d<k;d+=2)
dp[i][j][1] = (dp[i][j][1]+(dp[i][i+d][0]*(dp[i+d+1][j][0]+dp[i+d+1][j][1]))%mod)%mod;
dp[i][j][2] = (dp[i][j][0]+dp[i][j][1])%mod;
}
}
cout<<dp[1][n][2]<<endl;
}