题目
- (1)图中未探索区域是否存在一定不为雷的位置?
- (2)求已探索区域边缘所有可能的雷区分布。
- (3)求本局游戏可以获胜的概率(假设玩家不会犯低级失误)。
已知条件有:图中一共有15个空格,其中分为两个连通块,一个是14,另一个单独的1个,全图只剩下6个雷。
二、解决方法
2.1 分析题目
首先分析两个连通块的问题,这里很简单,只需要分两种情况讨论即可:
单独的连通块是雷。那么另一含有14个空格的连通块只有5个雷(6-1=5).
单独的连通块是数字3。那么另一还有14个空格的联通块只有6个雷。
可以发现,情况基本上一样,只是算法的参数不一样,比如我这里的开始进入dfs的参数为$dfs\left(a,6,1,1\right)$中的第二个参数是6,代表还剩下6个雷。那么在第一种情况下只需要重新带入$dfs\left(a,5,1,1\right)$即表示还剩下5个雷。
因为两种情况分清楚之后,以下无特殊说明只讨论含有14个空格的连通块。
建图的话则用二维数组即可,我用x表示“雷“,s表示空格,p表示无关紧要的或者是填入的数字,并且对空格标号。
import numpy as np
a = np.array([['3','3','4','3','3','2','1','1','1','2'],
['2','x','x','x','2','1','p','1','x','2'],
['3','4','s','5','x','2','1','3','3','2'],
['2','x','s','4','x','3','2','x','x','1'],
['3','x','s','s','s','s','s','s','3','2'],
['2','2','s','s','s','s','s','s','1','1'],
['p','p','p','p','p','p','p','p','p','p']])
pos = {
1: (2,2),#第一个空格位置在(2,2)
2: (3,2),
3: (4,2),
4: (5,2),
5: (4,3),
6: (5,3),
7: (4,4),
8: (5,4),
9: (4,5),
10: (5,5),
11: (4,6),
12: (5,6),
13: (4,7),
14: (5,7)#第十四个空格位置在(5,7)
}
2.2 搜索算法
算法则用深度优先搜索(DFS)加剪枝的方法,大致的思想是将还未填入数字或者雷的格子编号。先不论填入是对是错,对于每一个格子都有“雷“和”数字“的方法,在不剪枝的情况下则有$2^{14}$种情况,当14个格子都填入完毕之后,则进行Check()函数判断是否可行,可行则计数并且输出。
Check()函数即判断对于每一个格子的周围雷数是否等于当前格子的数字,如果有一个不满足则返回False,当全部的判断完毕之后都没有返回False,那么就返回True。
dx=[-1,-1,-1,0,0,1,1,1]
dy=[-1,0,1,-1,1,-1,0,1]
def Check(a):
for i in range(1,7):
for j in range(1,9):
x,y = i,j#位置
cnt_x = 0#周围雷的个数
if a[x][y] <='5' and a[x][y] >= '1':#如果是数字
for k in range(8):#判断八个方向
if a[x+dx[k]][y+dy[k]] == 'x':#判断八个方向
cnt_x += 1#雷数+1
if cnt_x != int(a[x][y]):#如果周围雷个数和数字不相等
return False#返回False
return True#返回True
然后就是整个搜索的过程,$dfs\left(a,res,i,num\right)$共有四个参数,$a$表示整张图,$res$表示还剩下多少个雷,$i$表示当前对于$pos$的第$i$位,通过$pos\left[i\right]$可以获取位置,$num$表示这个状态的编号。
ok_x表示填入雷是否正确,ok_p表示填入数字是否正确。这里有类型为字典的Type,用来存放当前状态为num的类型,一共分为6种:
1)$Type\left[num\right]=’11’$。表示ok_x=True,ok_p=True;
2)$Type\left[num\right]=’11’$。表示ok_x=True,ok_p=True;
3)$Type\left[num\right]=’11’$。表示ok_x=True,ok_p=True;
4)$Type\left[num\right]=’11’$。表示ok_x=True,ok_p=True;
5)$Type\left[num\right]=1$。表示当前已经填完,并且全部满足情况,是正确的图。
6)$Type\left[num\right]=0$。表示当前已经填完,但不全部满足情况,是错误的图。
其实这个类型加上dfs传参的第四个参数,传下一次要么是$num\ast2$要么是$num\ast2+1$,加上这个类型很像二叉树了。可以把填入雷当作左儿子,把填入数字当作右儿子,完全二叉树就是这样编号的。
其中有当剩下的雷数小于0的时候,则没必要往下填了,因为必定是错误的(实际上这里也可以不剪枝)。
if res<0:#剩下的雷数小于0
return False #返回False,剪枝
结束的时候即当i=15,也就是填完所有的格子之后再dfs的时候,只需要判断是否合法,如果合法的话那么就计数cnt+=1,并且输出和标记当前类型$Type\left[num\right]=1$,并且返回True,让上方的ok=True;否则标记当前类型$Type\left[num\right]=0$,并且返回False,让上方的ok=False。
if i-1 == len(pos):
if res == 0 and Check(a):#如果雷为0且Check返回正确
cnt += 1
Type[num] = 1#此时表示正确,则为1
print('cnt:',cnt,'\n',a,'\n',file=fp)#输出
return True#返回True,上一层的ok则可以接收到
Type[num] = 0#此时表示错误,则为0
return False#返回False,上一层的ok则可以接收到
接着就是填入雷或者数字,并且用ok_x和ok_p表示传下去的dfs是否合法,如果合法则返回True,否则返回False。
x,y = pos[i]#获取第i个空格位置
a[x][y] = 'x'#填入雷
ok_x = dfs(a,res-1,i+1,num*2)#进行深搜,结果返回至ok_x
a[x][y] = 'p'#填入数字
ok_p = dfs(a,res,i+1,num*2+1)#进行深搜,结果返回至ok_p
当dfs过后,我们再统计当前节点的类型,当前类型是否合法是需要下方的两个子结点(也就是填雷或者填数字),如果都不合法,那么这个节点肯定也不合法则需要返回False反馈给上方的节点。只要有一个合法,那么这个节点就是合法的,并且也要返回True回溯给上方节点。并且通过四种类型填入$Type\left[num\right]$中。
if ok_x == False and ok_p == False:#如果两个都不正确
Type[num]='00'#类型为'00'
return False#返回False
if ok_x == True and ok_p == True:
Type[num]='11'
if ok_x == True and ok_p == False:
Type[num]='10'
if ok_x == False and ok_p == True:
Type[num]='01'
#填入相应类型
return True#返回True
举个例子,下图就是我们理想的图片,当为1的时候即为填入雷,当为0的时候则表示填入数字。绿色代表往下有情况可行,橙色表示往下哪一条路都不合法。每一层表示对于每一个位置的情况,显然,这个树在这个题目里面是有14层深度的。
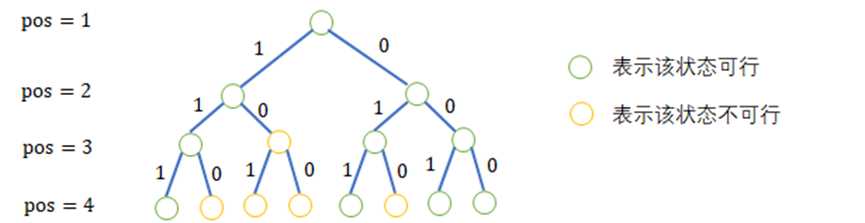
三、解决问题
3.1 问题一:图中未探索区域是否存在一定不为雷的位置?
通过我的搜索,当雷数为6个雷的时候,一共有52种情况;当雷数为5个雷的时候,一共有28种情况。总共80种情况,我们把每种情况的14个格子都进行判断,如果当前是雷那么就+1,如此80种情况下来,按照题意所说一定不为雷的位置来看的话,那么这个数将为0,依照此思想,我们进行统计。
只需要在dfs中判断合法的下方重新遍历一遍pos字典,判断如果是雷则计数加一,最后80种情况结束之后输出count查看。
if i-1 == len(pos):
if res == 0 and Check(a):#如果雷为0且Check返回正确
cnt += 1
Type[num] = 1#此时表示正确,则为1
print('cnt:',cnt,'\n',a,'\n',file=fp)#输出
for i in pos:
x,y = pos[i]
if a[x][y] == 'x':
count[i] += 1 #记录每个位置的雷出现次数
return True#返回True,上一层的ok则可以接收到
Type[num] = 0#此时表示错误,则为0
return False#返回False,上一层的ok则可以接收到
1到14出现次数分别为$\lbrace{40,40,40,40,20,28,20,28,30,28,30,28,20,60\rbrace}$,可以看出出现雷的次数至少为28,故没有可能有一定不为雷的位置。
3.2 问题二:求已探索区域边缘所有可能的雷区分布。
因为是边缘的,所以我只需要pos中的其中边缘的,也就是编号为$\lbrace{1,2,3,4,5,7,9,11,13\rbrace}$。
need = [1,2,3,4,5,7,9,11,13]#边缘
state = []#边缘的状态
我们在每次判断正确的时候将这个状态存下来,也就是每一位是x还是p。判断如果不在state中,那么就存入状态,否则不存入,因为已经重复了。
tmp = []
for i in need:
x,y = pos[i]
tmp.append(a[x][y])
if tmp not in state:
state.append(tmp)
return True
最后80种情况结束之后,我们来观察一共有10种情况。
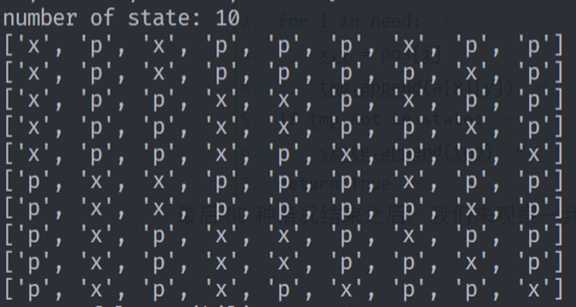
3.3 问题三:求本局游戏可以获胜的概率(假设玩家不会犯低级失误)。
这里假设玩家绝顶聪明,不会犯低级错误,也就是说玩家能够可以推出一颗树的状态,也就是之前那张图玩家是可以判断出来的。那么什么时候玩家会发生错误?
当玩家知道两条路都可以走的时候,就可能会发生错误,因为此时填入雷和不填入雷都是可能的。当玩家填入雷的时候,可能是他所想的那一条路,但是也许这个时候的棋盘那里就不是雷,所以——当两条路都可以走的时候,概率会减半。
但是,如果此时只有一条路可以走,那么聪明绝顶的玩家会一直按着那条路走,直到又有可能进行分叉,所以这个时候概率有需要有变化。

例如上图,当玩家直到第一个点往下两条路都可以走,那么这个时候就有可能犯错,正如上述所言,情况都可以的时候,是会有可能跟棋盘不一样的。但是如果看到pos=3的$\lbrace {1,1\rbrace}$路径的时候,发现只有1,也就是填入雷才有可能成功,聪明绝顶的玩家是不会选择橙色的点的。
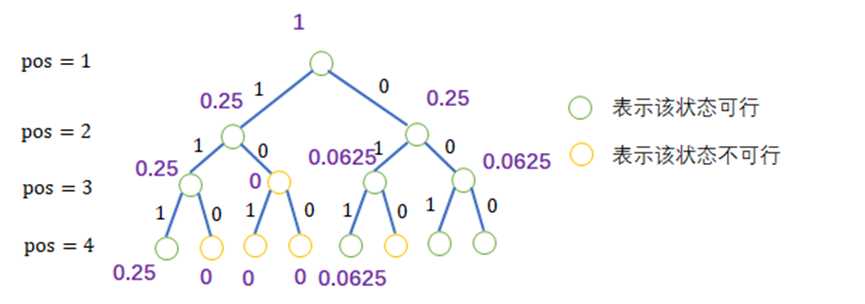
上图紫色代表概率,为什么我的第二层不是0.5而是0.25?需要除以4?那是因为概率应该是自下而上的总和,这里是分配到这一步的概率,还未统计。除以4是因为这里有可能犯错误,需要除以二,0.25+0.25=0.5,所以这一层pos=2的时候,概率是0.5(暂时)。
之所以说暂时,是因为只考虑到当前,并未往下递归完成后回溯统计,我们需要统计的是对于每一个节点,已知子结点之后两个子结点概率之和,比如还是路径$\lbrace { 1,1 \rbrace } $的pos=3的时候,这个时候的概率就是p=0.25+0。
所以当全部递归之后,到达底部,开始往上回溯统计概率,如果这条路走不通,那么概率当然是0,那么为什么要写0.25,0.0625呢?这相当于分配到当前节点的概率,经过判断之后,判断返回应该是当前的,还是0(代表不合法)。
例如上图的到达底部的结果应该是:
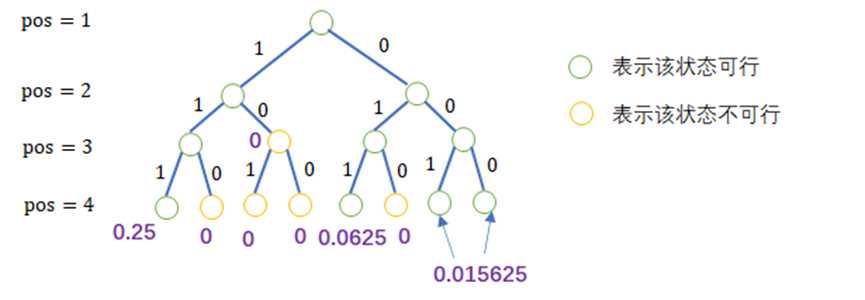
这些数字是自上而下分配到当前节点的概率(上述描述过),这个时候该统计概率并往上返回。
p1 = 0.0#表示填雷
p2 = 0.0#表示填数字
if Type[num] == '11':
p1 = calc(a,res-1,i+1,num*2,p/4.0)
p2 = calc(a,res,i+1,num*2+1,p/4.0)
if Type[num] == '10':
p1 = calc(a,res-1,i+1,num*2,p)
#p2 = 0
if Type[num] == '01':
#p1 = 0
p2 = calc(a,res,i+1,num*2+1,p)
return p1+p2
最后我们能统计出顶点的概率,代表这个图成功的概率。
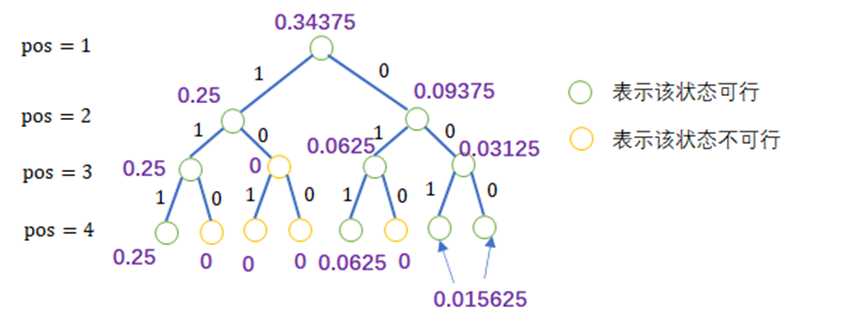
这样统计能够看出,这张图的玩家获胜的概率为0.34375。
至此,计算概率的方法大致统计出来了,基本思想就是递归和回溯的思想,在dfs的函数里面已经得出当前的状态,所以我们再写一个类似于dfs的函数calc统计即可。
possibility = {}
def calc(a,res,i,num,p):
if res<0:
return 0.0#保持一致
if i-1 == len(pos):
return p #返回概率
p1 = 0.0#表示填雷
p2 = 0.0#表示填数字
if Type[num] == '11':
p1 = calc(a,res-1,i+1,num*2,p/4.0)
p2 = calc(a,res,i+1,num*2+1,p/4.0)
if Type[num] == '10':
p1 = calc(a,res-1,i+1,num*2,p)
#p2 = 0
if Type[num] == '01':
#p1 = 0
p2 = calc(a,res,i+1,num*2+1,p)
return p1+p2
最后我们将$calc\left(a,6,1,1,1.0\right)$函数输出,能够得到此时的概率为:

当然,这个时候只是其中一种情况,也就是连通块为6个雷的时候,同样改一下参数能够求出$calc\left(a,5,1,1,1.0\right)$,此时概率为:

在第一次选择右下角是否为雷的时候,需要一次选择,这时候可能会出错,所以这个题的概率为:
$$
P=(0.02294921875+0.0478515625)/4=0.0177001953125
$$
四、计算结果
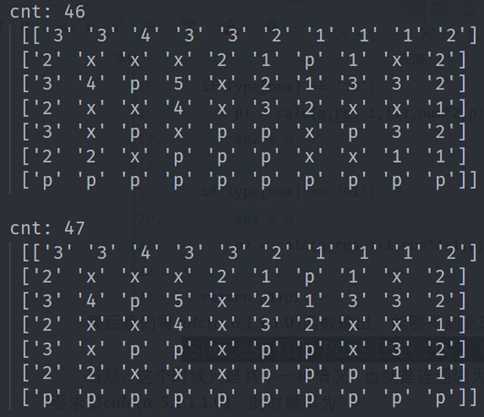
所有情况用文本形式保存,部分结果如下,可以得到所有情况(80种):
五、源代码
1. import numpy as np
2. a = np.array([['3','3','4','3','3','2','1','1','1','2'],
3. ['2','x','x','x','2','1','p','1','x','2'],
4. ['3','4','s','5','x','2','1','3','3','2'],
5. ['2','x','s','4','x','3','2','x','x','1'],
6. ['3','x','s','s','s','s','s','s','3','2'],
7. ['2','2','s','s','s','s','s','s','1','1'],
8. ['p','p','p','p','p','p','p','p','p','p']])
9.
10. pos = {
11. 1: (2,2),
12. 2: (3,2),
13. 3: (4,2),
14. 4: (5,2),
15. 5: (4,3),
16. 6: (5,3),
17. 7: (4,4),
18. 8: (5,4),
19. 9: (4,5),
20. 10: (5,5),
21. 11: (4,6),
22. 12: (5,6),
23. 13: (4,7),
24. 14: (5,7)
25. }
26.
27. dx=[-1,-1,-1,0,0,1,1,1]
28. dy=[-1,0,1,-1,1,-1,0,1]
29. count = {}
30. need = [1,2,3,4,5,7,9,11,13]#边缘
31. state = []#边缘的状态
32.
33. def Check(a):
34. for i in range(1,7):
35. for j in range(1,9):
36. x,y = i,j#位置
37. cnt_x = 0#周围雷的个数
38. if a[x][y] <='5' and a[x][y] >= '1':#如果是数字
39. for k in range(8):#判断八个方向
40. if a[x+dx[k]][y+dy[k]] == 'x':#判断八个方向
41. cnt_x += 1#雷数+1
42. if cnt_x != int(a[x][y]):#如果周围雷的个数和数字不相等
43. return False
44. tmp = []
45. for i in need:
46. x,y = pos[i]
47. tmp.append(a[x][y])
48. if tmp not in state:
49. state.append(tmp)
50. return True
51.
52. cnt = 0
53. Type = {}#Type[i]表示编号为i的下的情况
54. def dfs(a,res,i,num):
55. global cnt
56. if res<0:#剩下的雷数小于0
57. return False
58. if i-1 == len(pos):
59. if res == 0 and Check(a):#如果雷为0且Check返回正确
60. cnt += 1
61. Type[num] = 1#此时表示正确,则为1
62. print('cnt:',cnt,'\n',a,'\n',file=fp)#输出
63. for i in pos:
64. x,y = pos[i]
65. if a[x][y] == 'x':
66. count[i] += 1 #记录每个位置的雷出现次数
67. return True#返回True,上一层的ok则可以接收到
68. Type[num] = 0#此时表示错误,则为0
69. return False#返回False,上一层的ok则可以接收到
70.
71. x,y = pos[i]#获取第i个空格位置
72. a[x][y] = 'x'#填入雷
73. ok_x = dfs(a,res-1,i+1,num*2)#进行深搜,结果返回至ok_x
74. a[x][y] = 'p'#填入数字
75. ok_p = dfs(a,res,i+1,num*2+1)#进行深搜,结果返回至ok_p
76.
77. if ok_x == False and ok_p == False:#如果两个都不正确
78. Type[num]='00'#类型为'00'
79. return False#返回False
80. if ok_x == True and ok_p == True:
81. Type[num]='11'
82. if ok_x == True and ok_p == False:
83. Type[num]='10'
84. if ok_x == False and ok_p == True:
85. Type[num]='01'
86. #填入相应类型
87. return True#返回True
88.
89. possibility = {}
90. def calc(a,res,i,num,p):
91.
92. if res<0:
93. return 0.0#保持一致
94. if i-1 == len(pos):
95. return p #返回概率
96.
97. p1 = 0.0#表示填雷
98. p2 = 0.0#表示填数字
99. if Type[num] == '11':
100. p1 = calc(a,res-1,i+1,num*2,p/4.0)
101. p2 = calc(a,res,i+1,num*2+1,p/4.0)
102.
103. if Type[num] == '10':
104. p1 = calc(a,res-1,i+1,num*2,p)
105. #p2 = 0
106.
107. if Type[num] == '01':
108. #p1 = 0
109. p2 = calc(a,res,i+1,num*2+1,p)
110.
111. return p1+p2
112.
113. if __name__ == '__main__':
114. fp = open('D:/pyCode/output1.txt','w')
115. for i in range(0,15):
116. count[i] = 0
117. for i in range(0,40000):
118. possibility = 0.0
119. Type[i] = '00'
120. dfs(a,6,1,1)#需要改参数
121. #dfs(a,5,1,1)
122. print('cnt:',cnt)
123. print(count)
124. print('number of state:',len(state))
125. for i in state:
126. print(i)
127. print('Successful Possibility:',calc(a,6,1,1,1.0))#需要改参数
128.
129. fp.close()


