题意:
给你$n$个数,你需要平均分成两份,分别有$\frac{n}{2}$个,如果两个数满足下面等式,则会发生冲突,那么就需要在同一类才不会发生冲突:
$$
{\rm concat}(A_i,A_j)\times {\rm concat}(A_j,A_i)+A_iA_j \equiv Z \quad {\rm mod} \ 3
$$
思路:
举个例子${\rm concat}(123,456)=123456$,那么其实就是$123\times 10^3+456$,那么这个跟幂有关系,但是有一个很重要的$10\equiv 1\quad ({\rm mod}\ 3)$,所以有:
$$
10^p\equiv 1\quad ({\rm mod}\ 3)
$$
那么有
$$
{\rm concat}(A_i,A_j)=\overline{A_iA_j}=A_i+A_j\equiv Z\quad {\rm mod}\ 3
$$
所以最后化简可以为:

然后来看看$A_i$在模$3$意义下的关系:
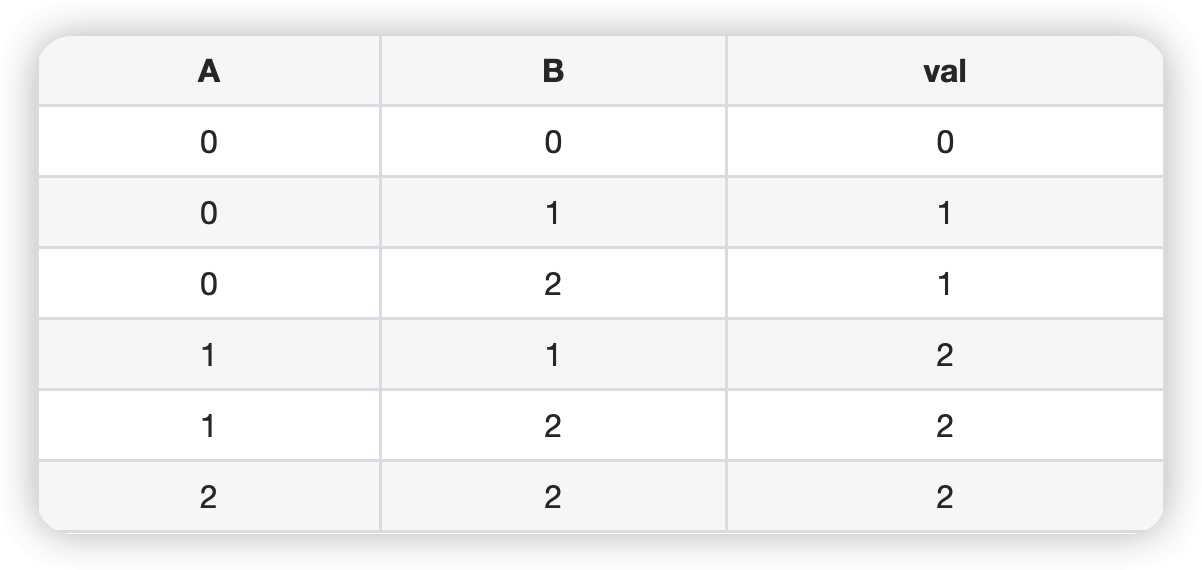
那么现在可以分成两种情况:
-
1)$val=0$的个数
res大于等于$\frac{n}{2}$
这个时候只需要令$Z=2$,res中输出$\frac{n}{2}$个$0$,其他输出$1$即可不发生碰撞 -
2)$val=0$的个数
res小于$\frac{n}{2}$
这些res个肯定需要输出$0$,其他的找$\frac{n}{2}-\rm res$出来即可。
代码:
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>a[i];
if (a[i]%3==0) cnt++;
}
if (cnt>=n/2)
{
cout<<2<<endl;
int res = n/2;
for (int i=1;i<=n;i++)
if (a[i]%3==0&&res) cout<<0,res--;
else cout<<1;
}
else
{
cout<<0<<endl;
int res = n/2-cnt;
for (int i=1;i<=n;i++)
if (a[i]%3==0) cout<<0;
else if (res) cout<<0,res--;
else cout<<1;
}
}
