题目
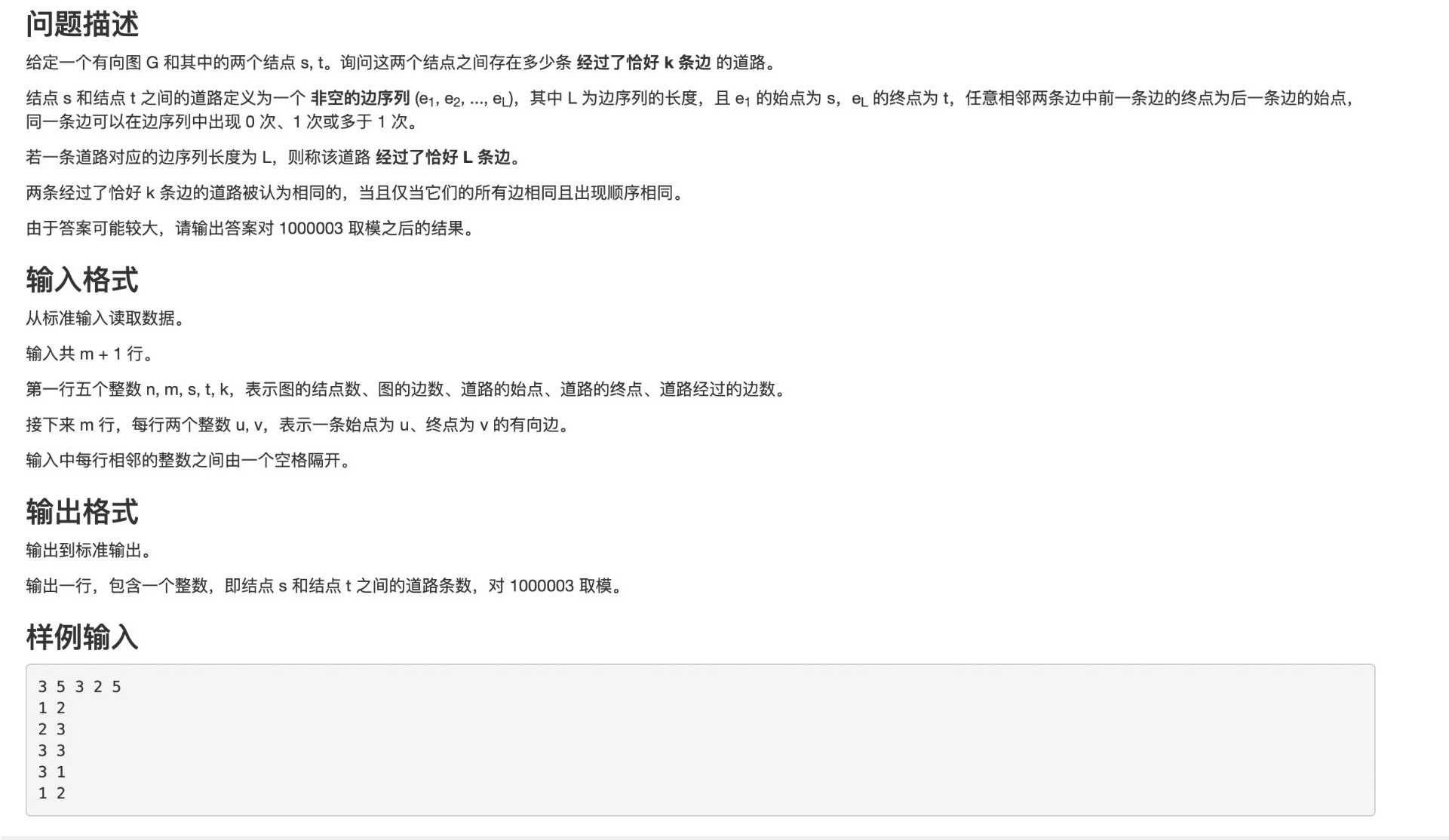
给定一个有向图G和其中的两个结点s,t。询问这两个结点之间存在多少条经过了恰好k条边的道路。
注意:包括重边和自环!
例如下图
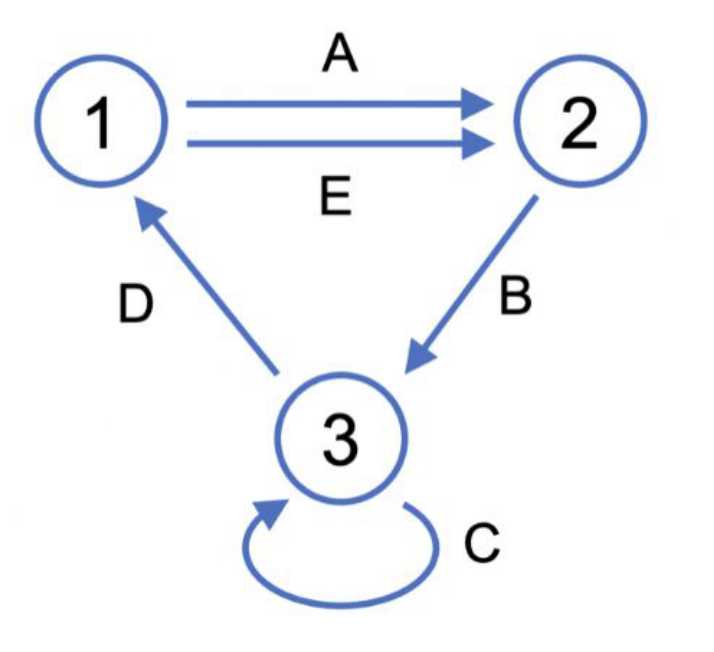
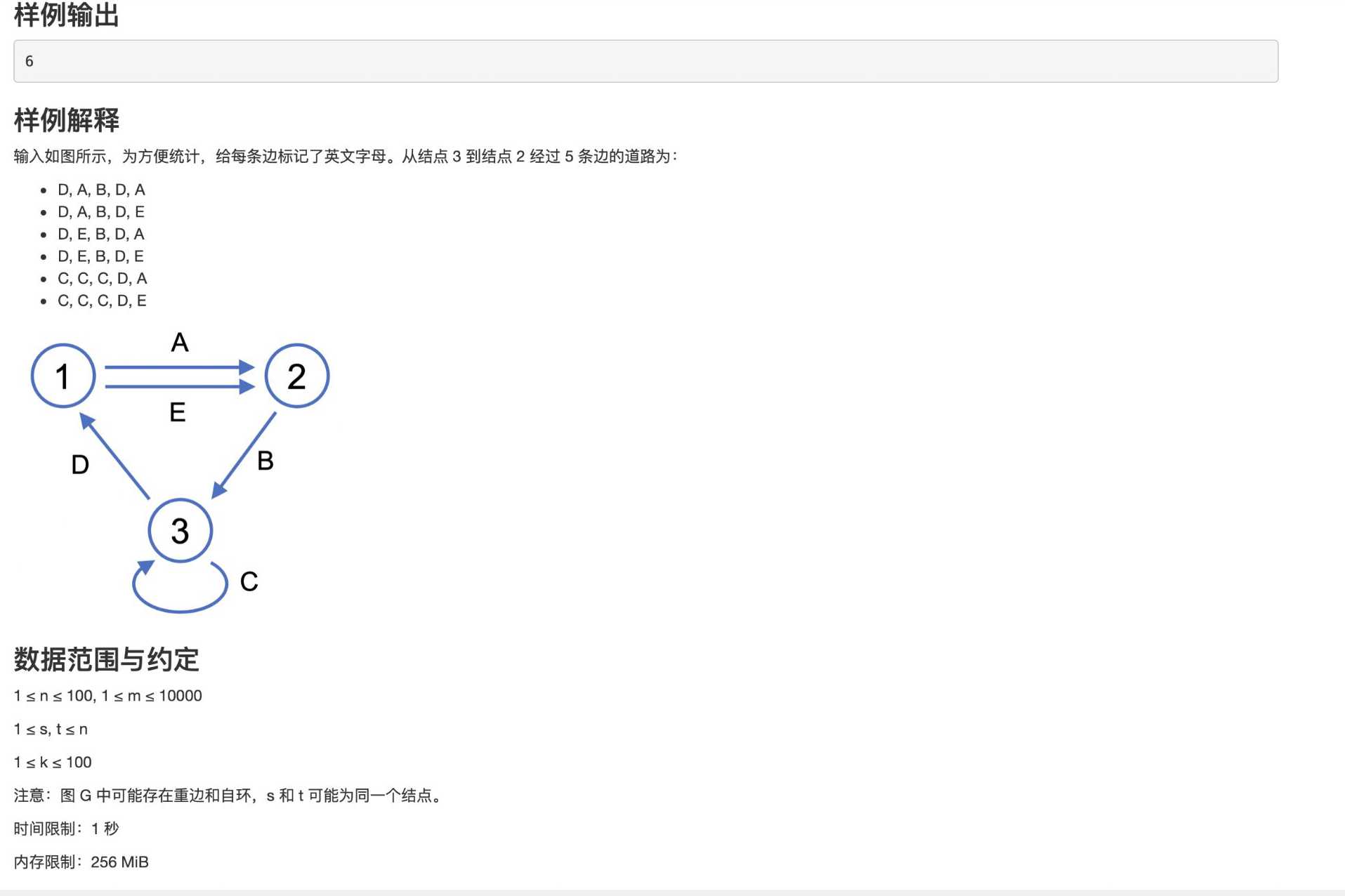
从3到2,长度为5,我们有6条道路,分别是:
1. D,A,B,D,A
2. D,A,B,D,E
3. D,E,B,D,A
4. D,E,B,D,E
5. C,C,C,D,A
6. C,C,C,D,E
思路
这个题一开始我是没思路的,实际上就是一个板子题...只需要学过离散数学...
把邻接矩阵写出来为

然后对其进行K次幂计算(可用矩阵快速幂),得到:
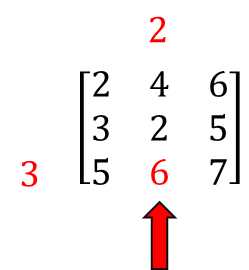
因为起点s=3,终点t=2,所以我们选择3行2列的6,答案也是6.
矩阵快速幂代码
#include<bits/stdc++.h>
using namespace std;
const int Mod=1000000007;
struct Matrix {
long long c[101][101];
} A,I;
long long n,k;
Matrix operator*(const Matrix &x,const Matrix &y) {
Matrix a;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
a.c[i][j]=0;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
for(int k=1; k<=n; k++) {
a.c[i][j]+=x.c[i][k]*y.c[k][j]%Mod;
a.c[i][j]%=Mod;
}
return a;
}
int main() {
cin>>n>>k;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
cin>>A.c[i][j];
for(int i=1; i<=n; i++)
I.c[i][i]=1;
while(k>0) {
if(k%2==1) I=I*A;
A=A*A;
k=k>>1;
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++)
cout<<I.c[i][j]<<' ';
cout<<endl;
}
return 0;
}
